前40分钟码完了前五题……最后还是没做出 F 题 TAT
也是第一次接触离线算法。听说 F 题可以用 树上莫队 和 主席树 做,但是我还没写,写完了如果能够记起来就再把博客补一下吧
· A题:T or T
- 题意
$n$ 个人出去旅行,可以选择以下方式:
- $n$ 个人都坐火车,每人会花费 $A$ 日元;
- $n$ 个人全部坐出租车,总共会花费 $B$ 日元;
求最小花费。
($1\leq n\leq 20,1\leq A,B\leq 50$)
| Input |
4 2 9 |
4 2 7 |
| Output |
8 |
7 |
(无解析可言)
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
|
#include<map>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){
int n,a,b;
scanf("%d%d%d",&n,&a,&b);
printf("%d\n",min(b,a*n));
return 0;
}
|
· B题:Good Distance
- 题意
定义在 $D$ 维空间的两点 $X=(x_1,x_2,x_3,…,x_D),Y=(y_1,y_2,y_3,…,y_D)$ 的距离为 $\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+…+(x_D-y_D)^2}$。
给定 $D$ ,给出 $N$ 个 $D$ 维的点,求有多少对不同的点的距离是整数。
($2\leq N\leq 10,1\leq D\leq10$,保证坐标的绝对值不超过 $20$)
| Input |
3 2
1 2
5 5
-2 8 |
3 4
-3 7 8 2
-12 1 10 2
-2 8 9 3 |
| Output |
1 |
2 |
(直接模拟,无解析可言)
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include<map>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10;
int n,d;
int pos[N+5][N+5];
int main(){
scanf("%d%d",&n,&d);
for(int i=1;i<=n;i++){
for(int j=1;j<=d;j++)
scanf("%d",&pos[i][j]);
}
int ans=0;
for(int u=1;u<=n;u++)
for(int v=u+1;v<=n;v++){
int tot=0;
for(int i=1;i<=d;i++)
tot+=(pos[u][i]-pos[v][i])*(pos[u][i]-pos[v][i]);
double _tot=sqrt(tot);
long long A=(long long)ceil(_tot),B=(long long)floor(_tot);
if(A*A==tot || B*B==tot)
ans++;
}
printf("%d\n",ans);
return 0;
}
|
· C题:Remainder Minimization 2019
一开始这道题吓了我一跳……
- 题意
给定 $L,R$ ,求对于 $i,j\in[L,R] 且 i\not=j$ ,$i\times j\bmod 2019$ 的最小值。
($0\leq L<R\leq2\times 10^9$)
| Input |
2020 2040 |
2000 2020 |
| Output |
2 |
0 |
| Explain |
i=2020,j=2021 |
i=2019,j=2020 |
- 解析
显然如果 $[L,R]$ 中存在 $2019$ 的倍数,那么 $i$ 取该数,$j$ 随便取,就可以使 $ij\bmod 2019=0$,这样当然是最小的。
考虑另外的情况——也就是 $[L,R]$ 中没有 $2019$ 的倍数……由于 $[L,R]$ 是一段连续的整数,如果没有 $2019$ 的倍数,那么……$[L,R]$ 中岂不是最多只有 $2018$ 个数?
(Right) 这么小的范围直接枚举就好了嘛。
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include<map>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int main(){
ll L,R;
scanf("%lld%lld",&L,&R);
if((L-1)/2019!=R/2019){
printf("0\n");
return 0;
}
ll ans=2019;
for(ll i=L;i<=R;i++)
for(ll j=i+1;j<=R;j++)
ans=min(ans,i*j%2019);
printf("%lld\n",ans);
return 0;
}
|
· D题:Rain Flows into Dams
一开始没看到 $N$ 是奇数,卡了一小会
- 题意
有 $N$ 座山围成环(第1座山的旁边是第N座和第2座),第 $i$ 座山和第 $(i+1)$ 座山之间是河流 $i$ (第 $N$ 座和第 $1$ 座之间是河流 $N$)。
如果第 $i$ 座山降了 $D_i$ 升雨,则它相邻的两条河流会分别涨水 $\frac {D_i}2$ 升。
现在给出第 $i$ 条河流涨了多少水,求出每座山各下了多少雨。
(保证N是奇数,$3\leq N<10^5$,河流的涨水量不超过 $10^9$)
| Input |
3
2 2 4 |
| Output |
4 0 4 |
- 解析
设第 $i$ 座山下了 $x_i$ 的雨,第 $j$ 条河流涨了 $y_j$ 的水。于是我们可以列方程——
接下来就是消元了——由 $(1)-(2)+(3)-…-(N-1)+(N)$ 可得:
解出 $x_1$;那其他元就可以依次代入方程解出了~
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include<map>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5;
int n;
ll cur;
ll t[N+5],x[N+5];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&t[i]),
cur+=(i%2? 1:-1)*2ll*t[i];
x[1]=cur/2;
for(int i=1;i<n;i++)
x[i+1]=2*t[i]-x[i];
for(int i=1;i<=n;i++)
printf("%lld%c",x[i],i==n? '\n':' ');
return 0;
}
|
· E题:Virus Tree 2
- 题意
给出一个 $N$ 个节点的树以及 $K$ 种不同的颜色,你需要给树的每个节点上色,使得任何距离小于等于 $2$ 的两不同点的颜色不同。求方案数模 $(10^9+7)$。
($1\leq N,K\leq 10^5$)
| Input |
4 3
1 2
2 3
3 4 |
5 4
1 2
1 3
1 4
4 5 |
| Output |
6 |
48 |
- 解析
考虑树上的一部分:
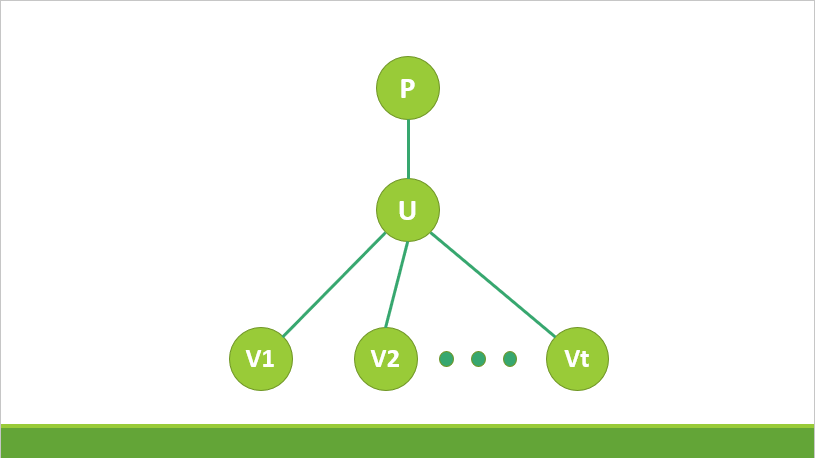
可以想到 V1,V2,…,Vt 总共可以取 $K-2$ 种颜色(也就是不能和 U,P 重复)。如果我们把给 V1,V2,…,Vt 涂色分步骤——也就是先涂 V1,再涂 V2,…,最后涂 Vt;
那么可以想到,V1 可以涂 $(K-2)$ 种颜色(不能和 P,U 相同);V2 可以涂 $(K-3)$ 种颜色 (不能和 P,U,V1)相同;…;Vt 可以涂 $(K-t-1)$ 种颜色。
但是根节点比较特殊,如果 U 是根节点,就不存在 P。特判即可。根据乘法原理乘起来即可
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include<map>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5;
const ll MOD=ll(1e9)+7;
int n;
ll ans,col;
vector<int> lnk[N+5];
void DFS(int u,int pre,int dep){
int cnt=0;
for(int it=0;it<lnk[u].size();it++){
int v=lnk[u][it];
if(v==pre) continue;
if(dep==1) ans=ans*max(0ll,col-1-cnt)%MOD;
if(dep>=2) ans=ans*max(0ll,col-2-cnt)%MOD;
DFS(v,u,dep+1);
cnt++;
}
}
int main(){
scanf("%d%lld",&n,&col);
for(int i=1;i<n;i++){
int u,v;scanf("%d%d",&u,&v);
lnk[u].push_back(v);
lnk[v].push_back(u);
}
ans=col%MOD;
DFS(1,0,1);
printf("%lld\n",ans);
return 0;
}
|
· F题:Colorful Tree
- 题意
给出一个有 $N$ 个节点的树,树的第 $i$ 条边有颜色 $c_i$ 和长度 $d_i$。
现给出 $Q$ 个询问,每个询问给出 $x,y,u,v$ :即如果将树上所有颜色为 $x$ 的边的长度改为 $y$ ,求 $u$ 到 $v$ 的简单路径的长度。
($2\leq N\leq 10^5,1\leq Q\leq 10^5,1\leq c_i<N,1\leq d_i\leq 10^4,1\leq y\leq 10^4$)
| Input |
5 3
1 2 1 10
1 3 2 20
2 4 4 30
5 2 1 40
1 100 1 4
1 100 1 5
3 1000 3 4 |
| Output |
130
200
60 |
- 解析
= 求解答案
令树的根是 rt ,记 u 和 v 的LCA为 lca ,那么我们可以计算出路径 (u,v)=(u,rt)+(v,rt)-2*(lca,rt),也就是说任意两点的路径信息都可以用点到根节点的路径的信息。
那么我们需要储存路径的什么信息?对于每个询问,我们需要知道路径(u,v)上颜色为 $x$ 的边的总长度collen、数量colcnt,以及路径 (u,v) 在未修改时的长度totlen——那么我们可以计算出修改后路径 (u,v)=totlen-collen+colcnt*y(也就是在原路径中删除颜色为 $x$ 的边,再把原来 colcnt 条颜色为 $x$ 的边的长度都改为 $y$ 加入路径中)。
但是颜色、询问和节点数都是 $10^5$ ,如果每个点都储存一个从它到根节点的路径的信息,是显然存不下的……
于是……
= 离线处理
由于 LCA 是 $O(\log n)$ (甚至离线还可以 $O(n)$,但是我不想写),我们想到可以先用 $O(Q\log n)$ 的时间复杂度把 $u,v,lca$ 都打一个标记。即对于第 i 个查询,在查询的 u,v 处分别打一个第 i 查询的标记 1,表示查询 i 的答案的一部分是需要加上路径 (u,rt),(v,rt) 的信息;在 lca 处打第 i 查询的标记2,表示查询 i 的答案的另一部分是减去两倍路径 (lca,rt) 的信息。
于是这样就实现了离线处理——
有什么作用呢?最显著的影响就是极大节省了内存:我们只需要在 DFS 时维护当前节点到 rt 的路径的信息就可以了。
em……详见代码……
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5;
struct EDGE{int u,v,col,len;}edg[N+5];
struct QUERY{int col,id,mdy,tag;};
vector<int> lnk[N+5];
vector<QUERY> qry[N+5];
int fa[N+5][20],dep[N+5],ans[N+5];
int n,m;
void Process(int u,int pre){
fa[u][0]=pre;dep[u]=dep[pre]+1;
for(int i=1;i<20;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=0;i<lnk[u].size();i++){
int v=edg[lnk[u][i]].u==u? edg[lnk[u][i]].v:edg[lnk[u][i]].u;
if(v==pre) continue;
Process(v,u);
}
}
int totfar,colcnt[N+5],collen[N+5];
void DFS(int u,int pre){
for(auto it : qry[u])
ans[it.id]+=it.tag*(totfar-collen[it.col]+colcnt[it.col]*it.mdy);
for(int i=0;i<lnk[u].size();i++){
int v=edg[lnk[u][i]].u==u? edg[lnk[u][i]].v:edg[lnk[u][i]].u;
if(v==pre) continue;
totfar+=edg[lnk[u][i]].len;
colcnt[edg[lnk[u][i]].col]++;
collen[edg[lnk[u][i]].col]+=edg[lnk[u][i]].len;
DFS(v,u);
totfar-=edg[lnk[u][i]].len;
colcnt[edg[lnk[u][i]].col]--;
collen[edg[lnk[u][i]].col]-=edg[lnk[u][i]].len;
}
}
int LCA(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=19;i>=0;i--)
if(dep[fa[u][i]]>=dep[v])
u=fa[u][i];
if(u==v) return u;
for(int i=19;i>=0;i--)
if(fa[u][i]!=fa[v][i])
u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int u,v,col,len;scanf("%d%d%d%d",&u,&v,&col,&len);
edg[i]=(EDGE){u,v,col,len};
lnk[u].push_back(i);lnk[v].push_back(i);
}
Process(1,0);
for(int i=1;i<=m;i++){
int u,v,col,len;
scanf("%d%d%d%d",&col,&len,&u,&v);
int lca=LCA(u,v);
qry[u].push_back((QUERY){col,i,len,1});
qry[v].push_back((QUERY){col,i,len,1});
qry[lca].push_back((QUERY){col,i,len,-2});
}
DFS(1,0);
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
|
The End
Thanks for reading!
Email: lucky_glass@foxmail.com ,欢迎提问~