OI - Abandoning Roads(Codeforces)

最后两天了呢……
做一些杂题练练手，然后就被这道题卡住了 :(

---

Part1. 题面

给出一个 $n$ 点 $m$ 边、带边权的无向连通图，边权只有两种取值 $a,b$ 且 $a<b$。

对于每个点，求出：在所有最小生成树中，它与节点 1 的距离最小是多少。

数据规模：$1\le n\le70,1\le m\le200,1\le a,b\le10^7$

---

Part2. 解析

注意到 n 非常的小，但是还没有小到 $O(2^n)$ 能过的程度。

Part2/1. 生成树方面

又注意到了题目中“边权只有 a,b 两个取值”这一条件，且 $a<b$。考虑 Kruskal 生成树的思想。

> Tab.
以下“A边/B边”分别指权为 a 和权为 b 的边。

Kruskal 中，会把较小边排在前面，也就是说，会优先考虑A边。于是可以先只用A边 生成一个森林，然后再用B边把这个森林连接成一棵树。换句话说，只用A边做生成树后，图中存在若干个连通块；然后再用B边把这些连通块连接起来。

注意到每一条A边都可能出现在最小生成树中 —— 如果加入A边 $(u,v)$ 时，u,v 已经处于一个连通块中了，那么我们可以删去现在 u,v 路径上的一条A边，然后再把 $(u,v)$ 这条边加进去（显然是等价的）。

再考虑连接B边：现在图上存在若干个连通块，不妨把每个连通块都缩成一个点，不影响结果。于是就是要在这张缩点之后的图上用B边生成树。

生成树的原则是，新增的边不能连接现在已经连通的两个点（不然就成环了）。根据这一点，可以得到以下两种 B 边都是不能连的（下图中绿边是A边，橙边是B边）：

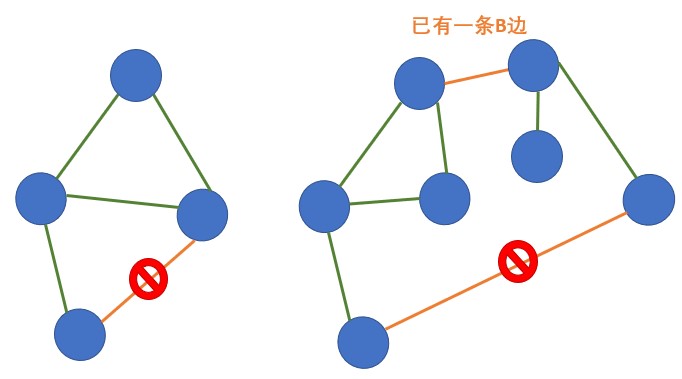
对于生成树，结论先推导到这里，也就是两种不可以连的B边。

Part2/2. 最短路方面

既然题面求所有节点在生成树上的最短距离……很容易想到最短路。而且是以节点 1 为起点的单源点最短路。

但是直接跑最短路就会有问题，因为最短路上的边一定要能够同时出现在最小生成树上。如果直接跑最短路，因为原图上的A边会比B边优先考虑出现在生成树中，但是不一定A边构成的路径比B边构成的路径优，比如下面这样：

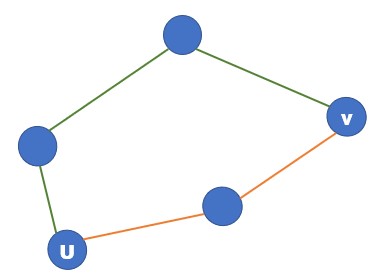
虽然 $a<b$，但是 $3a$ 可能大于 $2b$。如果直接跑最短路，找到两条B边构成的路径就错了，因为两条B边不可能同时出现在最短路中。
也就是对应了之前我们推导的“两种不能连的B边”的第二种。

反过来考虑什么最短路径是合法的：从 Dijkstra 的角度，用当前点 u 的距离 dis[u] 更新其他相邻的点 v 的距离 dis[v]。那么就必须要保证，如果 $(u,v)$ 是B边，那么 v 不能出现在已经到达过的连通块（指用 A边 构成的连通块）中。

这个时候注意到 $n$ 很小，就考虑状压我们已经到达过的连通块。但是连通块是数量 $O(n)$ 的，$2^{70}$ 连数组都开不下……

Part2/3. 状压优化

既然压不下，考虑不压缩一些连通块：

1. 单个节点的连通块，没有A边，不存在连接B边后会不合法的情况；
2. 两个节点的连通块，连通块中的唯一一条A边连接连通块中的点 $(u,v)$，那么这条A边一定是 $(u,v)$ 的最短路径，最短路更新时也不会取到B边，所以没有不合法情况；

诶，现在就只剩节点数 $\ge3$ 的连通块了，连通块数量就降低到了 $\left\lfloor\frac {70}3\right\rfloor=23$ 个，但是仍然不够，现在是时间复杂度的问题了……

那么能不能不压缩三个节点的连通块呢？

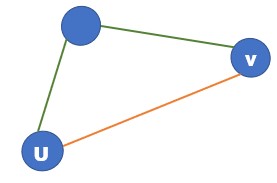
三个节点的连通块只存在这一种不合法情况，当 $2a>b$ 时。这种B边比较特殊，直接连接了同一个连通块中的两点，属于之前推导的”不合法的B边“中的第一种。
正因为比较特殊，可以直接把这种B边删去。于是三个节点的连通块就不用状压了。

现在连通块节点数 $\ge4$，连通块数量 $\left\lfloor\frac {70}4\right\rfloor=17$ 个，可以状压了！于是 f[i][S] 表示经过的连通块集合为 S 且当前在点 i 的最短距离，用堆优化 Dijkstra 跑最短路即可。

---

Part3. 源代码

/*Lucky_Glass*/
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=70,M=200;

struct DSU{
	int fa[N+3],siz[N+3];
	DSU(){
		for(int i=1;i<=N;i++){
			fa[i]=i;
			siz[i]=1;
		}
	}
	int FindFa(int u){return u==fa[u]? u:fa[u]=FindFa(fa[u]);}
	bool Merge(int u,int v){
		int fu=FindFa(u),fv=FindFa(v);
		if(fu==fv) return false;
		fa[fu]=fv;
		siz[fv]+=siz[fu];siz[fu]=0;
		return true;
	}
	int& operator [](int id){return fa[id];}
}Ds;
struct NODE{
	int to,len;
	NODE *nxt;
};
struct GRAPH{
	NODE pol[M*2+3],*head[N+3],*ncnt;
	GRAPH(){ncnt=pol;}
	void AddEdge(int u,int v,int len){
		NODE *p=++ncnt,*q=++ncnt;
		p->to=v;p->len=len;p->nxt=head[u];head[u]=p;
		q->to=u;q->len=len;q->nxt=head[v];head[v]=q;
	}
	NODE* operator [](int id){return head[id];}
}Gr;
struct STATU{
	int S,u,dis;
	STATU(){}
	STATU(int _S,int _u,int _d):S(_S),u(_u),dis(_d){}
	bool operator <(const STATU &B)const{return dis>B.dis;}
};

int n,m,A,B;
int id[N+3],nid;
int dis[N+3][1<<17],ans[N+3];
bool fix[N+3][1<<17];

int main(){
	memset(dis,0x3f,sizeof dis);
	scanf("%d%d%d%d",&n,&m,&A,&B);
	for(int i=1;i<=m;i++){
		int u,v,len;scanf("%d%d%d",&u,&v,&len);
		if(len==A) Ds.Merge(u,v);
		Gr.AddEdge(u,v,len);
	}
	memset(id,-1,sizeof id);
	for(int i=1;i<=n;i++)
		if(Ds[i]==i && Ds.siz[i]>3)
			id[i]=nid++;
	memset(dis,0x3f,sizeof dis);
	memset(ans,0x3f,sizeof ans);
	priority_queue< STATU > que;
	Ds.FindFa(1);
	if(id[Ds[1]]!=-1)
		que.push(STATU(1<<id[Ds[1]],1,dis[1][1<<id[Ds[1]]]=0));
	else
		que.push(STATU(0,1,dis[1][0]=0));
	while(!que.empty()){
		STATU u=que.top();que.pop();
		if(fix[u.u][u.S]) continue;
		fix[u.u][u.S]=true;
		for(NODE *it=Gr[u.u];it;it=it->nxt){
			int v=it->to;
			Ds.FindFa(v);
			if(Ds[u.u]==Ds[v] && it->len==B) continue;
			if(it->len==B && id[Ds[v]]!=-1 && (u.S&(1<<id[Ds[v]]))) continue;
			int now=dis[u.u][u.S]+it->len,S_=u.S;
			if(id[Ds[v]]!=-1) S_|=1<<id[Ds[v]];
			if(!fix[v][S_] && now<dis[v][S_]){
				dis[v][S_]=now;
				que.push(STATU(S_,v,dis[v][S_]));
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int S=0;S<(1<<nid);S++)
			ans[i]=min(ans[i],dis[i][S]);
		printf("%d",ans[i]);
		if(i==n) printf("\n");
		else printf(" ");
	}
	return 0;
}

---

The End

Thanks for reading!

gugugu