<题面链接> 提取码:7puf
Part1. 游记
Day11 的游记被我吃了……不过确实没什么可写的……
|・ω・\)
感觉这几天状态都不是特别好,想到的方法和正解都不怎么沾边……
有一点恶心……
不过还好还有 3 天就可以回去了。
听说最后走的一天要考试诶……(就不能让我高高兴兴地回去吗)
但是感觉其他同学的状态开始好起来了,但是我这边还是没有什么起色(慌的一B :<)
听旁边新疆的同学说这场模拟赛组题人示意出题人把题出难一点,不要这么多一两百分的……
然后出题人回应,这次第三题有人考场 AC 我直播 **
……然后就这样了
Part2. Solution
ai……我还是个 OIer……还是写题解去吧
T1. 迷宫(maze)
[Experience]
成功地注意到迷宫的行数很小,然后就没有然后了,脑子里一团浆糊,本来想写一个倍增(怎么又是倍增???),然后介于之前写倍增写炸然后还没有暴力的分高,就放弃了,最后就写了一个大暴力 QwQ
[Solution]
迷宫的行数很小确实很重要。
由于小奇不能往左走,所以每次询问,小奇的行走范围就被限制在了第 b 列和第 d 列之间。这样一个区间用什么来维护呢?
——线段树。
线段树里的每一个节点 [l,r] 里维护一个数组 go[i][j] 表示 从第 l 列第 i 行走到第 r 列第 j 行的最小步数,不能到达为 -1。
一开始可以 $O(n^2)$ 处理出单列的 go 数组,所以构建线段树的复杂度是 $O(m\log_2(m)n^3)$ ,刚好够。
于是考虑合并两个区间 [l,m],[m+1,r],于是考虑中间的一个转移点 k,即“先从第 l 列第 i 行走到第 m 列第 k 行,然后走一步走到第 m+1 列第 k 行,最后再从第 m+1 列第 k 行走到第 r 列第 j 行”。合并一次复杂度为 $O(n^3)$。
查询即找到区间 [b,d] 对应的 go 数组,输出 go[a][c] 即可,时间复杂度 $O(\log_2mn^3)$ 。
修改即先修改第 b 列单行的 go 数组,然后线段树里递归回来时合并更新。
[Source]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int R=5,C=200000;
int rol,col,qry;
bool maz[R+3][C+3];
struct NODE{int go[R][R];};
struct SEGMENTTREE{
NODE nod[C*4+3];
NODE Merge(NODE v1,NODE v2){
NODE ret;
for(int x=0;x<rol;x++)
for(int y=0;y<rol;y++){
ret.go[x][y]=-1;
for(int z=0;z<rol;z++){
if(v1.go[x][z]==-1 || v2.go[z][y]==-1) continue;
if(ret.go[x][y]==-1) ret.go[x][y]=v1.go[x][z]+v2.go[z][y]+1;
else ret.go[x][y]=min(ret.go[x][y],v1.go[x][z]+v2.go[z][y]+1);
}
}
return ret;
}
void Build(int u,int lef,int rig){
if(lef==rig){
for(int i=0;i<rol;i++){
bool fail=false;
for(int j=i;j<rol;j++){
fail|=(!maz[j][lef]);
if(fail) nod[u].go[i][j]=nod[u].go[j][i]=-1;
else nod[u].go[i][j]=nod[u].go[j][i]=j-i;
}
}
return;
}
int mid=(lef+rig)>>1;
Build(u<<1,lef,mid);Build(u<<1|1,mid+1,rig);
nod[u]=Merge(nod[u<<1],nod[u<<1|1]);
}
NODE Query(int u,int lef,int rig,int L,int R){
if(L<=lef && rig<=R) return nod[u];
int mid=(lef+rig)>>1;
if(mid<L) return Query(u<<1|1,mid+1,rig,L,R);
if(R<mid+1) return Query(u<<1,lef,mid,L,R);
return Merge(Query(u<<1,lef,mid,L,R),Query(u<<1|1,mid+1,rig,L,R));
}
void Modify(int u,int lef,int rig,int pos){
if(pos<lef || rig<pos) return;
if(lef==rig){
for(int i=0;i<rol;i++){
bool fail=false;
for(int j=i;j<rol;j++){
fail|=(!maz[j][lef]);
if(fail) nod[u].go[i][j]=nod[u].go[j][i]=-1;
else nod[u].go[i][j]=nod[u].go[j][i]=j-i;
}
}
return;
}
int mid=(lef+rig)>>1;
Modify(u<<1,lef,mid,pos);
Modify(u<<1|1,mid+1,rig,pos);
nod[u]=Merge(nod[u<<1],nod[u<<1|1]);
}
}seg;
int main(){
freopen("maze.in","r",stdin);
freopen("maze.out","w",stdout);
scanf("%d%d%d",&rol,&col,&qry);
for(int i=0;i<rol;i++)
for(int j=1;j<=col;j++)
scanf("%d",&maz[i][j]);
seg.Build(1,1,col);
for(int t=0;t<qry;t++){
int tmp;scanf("%d",&tmp);
if(tmp==1){
int x,y;scanf("%d%d",&x,&y);
x--;
maz[x][y]=!maz[x][y];
seg.Modify(1,1,col,y);
}
else{
int Sx,Sy,Ex,Ey;
scanf("%d%d%d%d",&Sx,&Sy,&Ex,&Ey);
Sx--;Ex--;
NODE res=seg.Query(1,1,col,Sy,Ey);
printf("%d\n",res.go[Sx][Ex]);
}
}
return 0;
}
|
T2. 猛汉王(mhw)
[Experience]
这道题好神仙啊,考场上没有一点思路,被曼哈顿距离卡死了。
结果正解用切比雪夫距离转换了曼哈顿距离,就可以做了……
(总觉得这种转换以前见过,但是考试没想起来)
[Solution]
下面把猛汉称为“点”,有接击瓶的称为黑色点,反之称为白色点;
把两点的曼哈顿距离写为 d(u,v)
方便叙述
= 转化问题
定义 $cov(u)$ 表示与 $u$ 颜色不同、且曼哈顿距离小于等于 $D$ 的点的个数;
当 $u,v$ 颜色相同时,定义 $cov(u,v)$ 表示与 $u,v$ 颜色不同、且距离 $u,v$ 的距离都小于等于 $D$ 的点的个数。
现在考虑颜色相同的两点 $u,v$ 的压制关系:
如果 $u,v$ 都是黑点:
当 $u$ 压制 $v$ 时,对答案的贡献为 $cov(v)-cov(u,v)$,即与 $v$ 的距离小于等于 $D$、且与 $u$ 的距离大于 $D$ 的白点的个数;
当 $v$ 压制 $u$ 时,对答案的贡献为 $cov(u)-cov(u,v)$,字面理解类似于上面的情况;
如果 $u,v$ 都是白点:
当 $u$ 压制 $v$ 时,对答案贡献为 $cov(u)-cov(u,v)$;
当 $v$ 压制 $u$ 时,对答案贡献为 $cov(v)-cov(u,v)$;
由于不同的两对点之间互不影响,所以我们可以单独考虑每一对颜色相同的点的压制关系,则
Tab. 上面的 $\mathbb W,\mathbb B$ 分别是白色点和黑色点集合。
那么现在问题就是要求 $cov()$ 。
= 转化距离
由于曼哈顿距离并不好处理,我们引入新的距离 —— 切比雪夫距离:
$(x_1,y_1),(x_2,y_2)$ 的切比雪夫距离为 $\max\{|x_1-x_2|,|y_1-y_2|\}$
我们可以这样转换:新建一个坐标系,将原坐标系里的 点$(x,y)$ 变为点 $(x+y,x-y)$ 放进新坐标系里(换成 $(x-y,x+y)$ 也可以)。
我们发现原坐标系里的两点 $(x_1,y_1),(x_2,y_2)$ 的曼哈顿距离为 $|x_1-x_2|+|y_1-y_2|$ ,而这两个点在新坐标系里的切比雪夫距离为 $\max\{|(x_1+y_1)-(x_2+y_2)|,|(x_1-y_1)-(x_2-y_2)|\}$ 。
讲课的神犇说:“如果你知道绝对值不等式,你就会知道 $|x_1-x_2|+|y_1-y_2|=\max\{|(x_1+y_1)-(x_2+y_2)|,|(x_1-y_1)-(x_2-y_2)|\}$”。由于我不知道绝对值不等式,这里就不多加赘述了……(免得出锅)
也就是说原坐标系的曼哈顿距离等于新坐标系里的切比雪夫距离。
切比雪夫距离要好处理许多,根据定义,不难发现对于一个点 $u$,切比雪夫距离小于等于 $D$ 的点在以 $u$ 为中心的边长为 $2D$ 的正方形中。也就是下面这样:
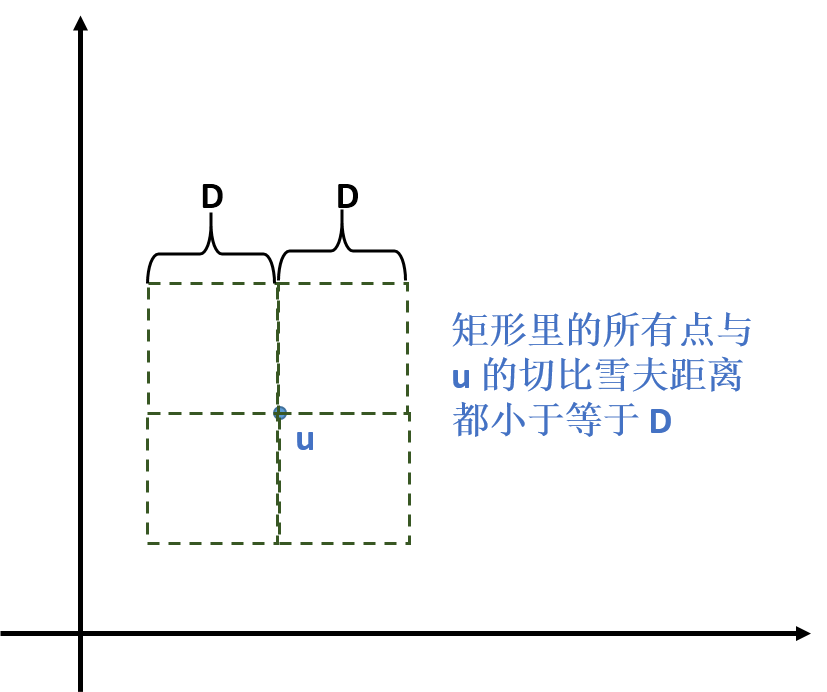
于是我们要对于每个点,统计以它为中心的这样一个正方形中,异色点的个数,也就是 $cov()$。注意到正方形的边长总是 $2D$,所以我们可以考虑滑窗——单点修改、区间查询,用BIT就可以做(感谢树状数组为我节省这么多的码量)
求出 $cov()$ 过后这道题就没有别的东西了……
[Source]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
|
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define lowbit(x) (x&-x)
#define uniID(a,b) (lower_bound(a.begin(),a.end(),b)-a.begin())
const int N=1e5;
typedef long long ll;
struct EP{ll x,y;}EPa[N+3],EPb[N+3];
bool cmpEPx(EP A,EP B){return A.x<B.x;}
ll tre[6*N+3],ntre;
void ModifyBIT(int pos,int val){
while(pos<=ntre){
tre[pos]+=val;
pos+=lowbit(pos);
}
}
ll QueryBIT(int pos){
int ret=0;
while(pos){
ret+=tre[pos];
pos-=lowbit(pos);
}
return ret;
}
ll cva[2*N+3],cvb[2*N+3];
int na,nb;
ll D;
vector<ll> uniy;
queue<int> que;
int main(){
freopen("mhw.in","r",stdin);
freopen("mhw.out","w",stdout);
scanf("%d%d%lld",&na,&nb,&D);
for(int i=1;i<=na;i++){
ll x,y;scanf("%lld%lld",&x,&y);
EPa[i].x=x+y;EPa[i].y=x-y;
uniy.push_back(EPa[i].y);
uniy.push_back(EPa[i].y+D);
uniy.push_back(EPa[i].y-D-1);
}
for(int i=1;i<=nb;i++){
ll x,y;scanf("%lld%lld",&x,&y);
EPb[i].x=x+y;EPb[i].y=x-y;
uniy.push_back(EPb[i].y);
uniy.push_back(EPb[i].y+D);
uniy.push_back(EPb[i].y-D-1);
}
sort(uniy.begin(),uniy.end());
uniy.erase(unique(uniy.begin(),uniy.end()),uniy.end());
ntre=uniy.size();
sort(EPa+1,EPa+na+1,cmpEPx);
sort(EPb+1,EPb+nb+1,cmpEPx);
for(int i=1,pos=1;i<=na;i++){
while(pos<=nb && EPb[pos].x<=EPa[i].x+D)
ModifyBIT(uniID(uniy,EPb[pos].y),1),que.push(pos++);
while(!que.empty() && EPb[que.front()].x<EPa[i].x-D)
ModifyBIT(uniID(uniy,EPb[que.front()].y),-1),que.pop();
cva[i]=QueryBIT(uniID(uniy,EPa[i].y+D))-QueryBIT(uniID(uniy,EPa[i].y-D-1));
}
while(!que.empty())
ModifyBIT(uniID(uniy,EPb[que.front()].y),-1),que.pop();
for(int i=1,pos=1;i<=nb;i++){
while(pos<=na && EPa[pos].x<=EPb[i].x+D)
ModifyBIT(uniID(uniy,EPa[pos].y),1),que.push(pos++);
while(!que.empty() && EPa[que.front()].x<EPb[i].x-D)
ModifyBIT(uniID(uniy,EPa[que.front()].y),-1),que.pop();
cvb[i]=QueryBIT(uniID(uniy,EPb[i].y+D))-QueryBIT(uniID(uniy,EPb[i].y-D-1));
}
ll MxAns=0,MnAns=0;
sort(cva+1,cva+na+1);
sort(cvb+1,cvb+nb+1);
for(int i=1;i<=na;i++)
MxAns+=(1ll*(i-1))*cva[i],
MnAns+=(1ll*(na-i))*cva[i];
for(int i=1;i<=nb;i++)
MxAns+=(1ll*(i-1))*cvb[i],
MnAns+=(1ll*(nb-i))*cvb[i];
for(int i=1;i<=na;i++){
if(cva[i]&1){
MxAns-=(1ll*cva[i]-1ll)/2ll*(cva[i]);
MnAns-=(1ll*cva[i]-1ll)/2ll*(cva[i]);
}
else{
MxAns-=(1ll*cva[i])/2ll*(cva[i]-1ll);
MnAns-=(1ll*cva[i])/2ll*(cva[i]-1ll);
}
}
for(int i=1;i<=nb;i++){
if(cvb[i]&1){
MxAns-=(1ll*cvb[i]-1ll)*(cvb[i])/2ll;
MnAns-=(1ll*cvb[i]-1ll)*(cvb[i])/2ll;
}
else{
MxAns-=(1ll*cvb[i])*(cvb[i]-1ll)/2ll;
MnAns-=(1ll*cvb[i])*(cvb[i]-1ll)/2ll;
}
}
printf("%lld %lld\n",MnAns,MxAns);
return 0;
}
|
T3. 工厂(factory)
[Experience] 被我吃了 (* ̄ω ̄)
[Solution]
考虑把原图看成一个 X部有 $n$ 个点,表示 $n$ 个员工、Y部有 $n$ 个点,表示 $n$ 台机器 的二分图。如果工人 u 会机器 v,则存在边 <u,v> 。
根据题意,再通过别人的一番论证(?),我们可以知道我们需要给二分图加上一些边(也就是让工人学会某个机器),使每个连通块都是一个完全二分图(也就是 X部的每个点与Y部的每个点都连了边)。我们要加尽量少的边,使得二分图满足上述要求。其实也就是要让加了边过后的二分图的边数尽可能少。
在还没有加边的时候,设原二分图中有 $m$ 个连通块,第 $i$ 个连通块表示为二元组 $(x_i,y_i)$ ,含义为连通块包含 $x_i$ 个 X部 的点和 $y_i$ 个 Y部 的点。
我们要把这些连通块划分为若干个集合,每个集合里的连通块的 $x_i$ 之和要等于 $y_i$ 之和相等。在满足上述条件的情况下,要使得所有连通块的总边数最小,也就是要让下述式子最小($\mathbb S$ 是分出来的集合):
考虑 DP —— f[S][i] 表示 S (S是压缩的状态)中的每个连通块都已经分配给集合,且现在正在分配的集合的 $x_i$ 之和为 $i$ 的最小花费。
于是就有两种转移:
如果当前 S 是一个合法状态(即 S 中的 $x_i$之和 等于 $y_i$之和),则可以将任意的 f[S][i] 转移到 f[S][0],代价为 $i^2$ ,即:
f[S][0]=min(f[S][0],f[S][i]+i*i)
将第 j 个连通块加入 S(原本 S 中没有 j),转移到 f[S+j][i+x[j]] ,没有花费(因为还没有确定当前正在分配的集合),即:
f[S+j][i+x[j]]=min(f[S+j][i+x[j]],f[S][i])
但是我们发现——连通块最大可以达到 60 个……(也就是原来的二分图里面没有边),状态压缩不下。
于是我们考虑换一种压缩的方式:我们发现若 $x_i=x_j$ 且 $y_i=y_j$ 的两个连通块 $i,j$ 的本质是相同的,而本质不同的连通块很少,可以压缩。
[Source]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=30,LIM=1e6;
struct PAIR{
int x,y;
PAIR(){}
PAIR(int _x,int _y):x(_x),y(_y){}
};
struct MERGESET{
int fa[2*N+3],cntx[2*N+3],cnty[2*N+3];
int FindFa(int x){
if(fa[x]==x) return x;
return fa[x]=FindFa(fa[x]);
}
void Merge(int x,int y){
int fx=FindFa(x),fy=FindFa(y);
if(fx==fy) return;
fa[fx]=fy;
cntx[fy]+=cntx[fx];cntx[fx]=0;
cnty[fy]+=cnty[fx];cnty[fx]=0;
}
}mrg;
PAIR pr[2*N+3];
bool vis[2*N+3];
char inpstr[N+3];
int cpr[2*N+3],f[LIM][N+3],jz[2*N+3];
int n,npr,inf,cnt1;
int Number(int S,int pos){
return S%jz[pos+1]/jz[pos];
}
int CntXS(int S){
int ret=0;
for(int i=1;i<=npr;i++){
int num=Number(S,i);
ret+=num*pr[i].x;
}
return ret;
}
int CntYS(int S){
int ret=0;
for(int i=1;i<=npr;i++){
int num=Number(S,i);
ret+=num*pr[i].y;
}
return ret;
}
int LMin(int a,int b){
if(a<b) return a;
return b;
}
int main(){
freopen("factory.in","r",stdin);
freopen("factory.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n+n;i++)
mrg.fa[i]=i,mrg.cntx[i]=(i<=n),mrg.cnty[i]=(i>n);
for(int i=1;i<=n;i++){
scanf("%s",inpstr+1);
for(int j=1;j<=n;j++)
if(inpstr[j]=='1')
mrg.Merge(i,j+n),
cnt1++;
}
for(int i=1;i<=n+n;i++){
int Fi=mrg.FindFa(i);
if(vis[Fi]) continue;
vis[Fi]=true;
bool fid=false;
for(int i=1;i<=npr && !fid;i++)
if(pr[i].x==mrg.cntx[Fi] && pr[i].y==mrg.cnty[Fi]){
fid=true;
cpr[i]++;
}
if(!fid){
pr[++npr]=PAIR(mrg.cntx[Fi],mrg.cnty[Fi]);
cpr[npr]=1;
}
}
jz[1]=1;
for(int i=2;i<=npr+1;i++) jz[i]=jz[i-1]*(cpr[i-1]+1);
memset(f,0x3f,sizeof f);inf=f[0][0];
f[0][0]=0;
for(int S=0;S<jz[npr+1];S++){
int cxs=CntXS(S),cys=CntYS(S);
if(cxs==cys)
for(int j=0;j<cxs;j++)
f[S][cxs]=min(f[S][cxs],f[S][j]+(cxs-j)*(cxs-j));
for(int j=0;j<=n;j++){
if(f[S][j]==inf) continue;
for(int i=1;i<=npr;i++){
if(Number(S,i)<cpr[i]){
int S_=S+jz[i];
f[S_][j]=LMin(f[S_][j],f[S][j]);
}
}
}
}
printf("%d\n",f[jz[npr+1]-1][n]-cnt1);
return 0;
}
|
The End
Thanks for reading!
Email: lucky_glass@foxmail.com,欢迎提问!
