前行 - CF Round 572 (Div2) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

前行 - CF Round 572 (Div2)

发表于 更新于 分类于 Valine：

最后 $3$ 题真的没有想到……竟然这么多数学题……

成功地把这场 CF Round 打成了手速场（还好没掉 Rating）

· A题：Keanu Reeves

- 题意

给出一个长度为 $n$ 的 01 字符串，你需要将原字符串分成若干段，使得每一段中 0 和 1 的个数不相等。要求分成的段数尽可能少，且输出分割的方案（如果有多种段数最少的方式，输出任意一个）。

[Input]
6
100011

[Output]
2
100 011

- 解析

可以证明最后分成的段数不超过 $2$ 。

  1. 如果原串中的 0 和 1 的个数就不同，那么不用分段，直接原串就是答案。

  2. 如果相同，则原串的长度一定是偶数。而我们知道，长度为奇数的 01 串中，0 和 1 的数量不可能相等；所以我们只要把第一段的长度取一个奇数就可以了，剩下的数就是第二段（因为原串长度是偶数，第一段长度是奇数则第二段长度也是奇数）

- 源代码

写复杂了，不要在意……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
int len,tot0,tot1;
string str;
int main(){
	scanf("%d",&len);cin>>str;
	for(int i=0;i<len;i++)
		tot0+=str[i]=='0',
		tot1+=str[i]=='1';
	if(tot0!=tot1){
		printf("1\n");
		cout<<str<<endl;
		return 0;
	}
	int cnt0=0,cnt1=0;
	printf("2\n");
	for(int i=0;i<len;i++){
		cnt0+=str[i]=='0';
		cnt1+=str[i]=='1';
		int _cnt0=tot0-cnt0,
			_cnt1=tot1-cnt1;
		if(_cnt0!=_cnt1 && cnt0!=cnt1){
			cout<<str.substr(0,i+1)<<" "<<str.substr(i+1,len-i-1)<<endl;
			return 0;
		}
	}
	return 0;
}

· B题：Number Circle

- 题意

给出 $n$ 个正整数，将这 $n$ 个数排成环，使得环上的每一个数严格小于与它相邻的两个数之和。

问是否能够构造出一个方案，若可以，输出方案（任意一个）。

Input 3
2 4 3		 4
1 10 100 1000
Output YES
4 2 3		 NO

- 解析

考虑下述做法：

img1

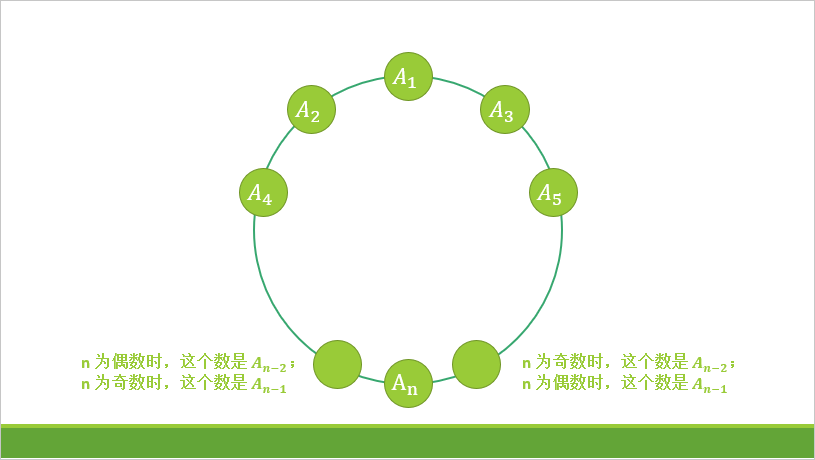
把所有数从小到大排序，并设第 $i$ 个数为 $A_i$，先放置 $A_1$；然后把 $A_2$ 放在 $A_1$ 左边、$A_3$ 放在 $A_1$ 右边；把 $A_4$ 放在 $A_2$ 左边、$A_5$ 放在 $A_3$ 右边……直到放完所有数。

我们来证明一下：

  1. 对于 $A_i(i\leq n-2)$ ，它旁边有 $A_{i+2}$ ，由于 $A_{i+2}\ge A_i$ 且 $A_i$ 另一边的数是正数，则 $A_i$ 旁边的两数之和一定大于 $A_i$；
  2. 对于 $A_{n-1}$ ，它旁边有 $A_n$ ，由于 $A_n\ge A_{n-1}$ 且 $A_{n-1}$ 另一边的数是正数，则 $A_{n-1}$ 同样满足条件；
  3. 对于 $A_n$，它旁边的数是 $A_{n-1},A_{n-2}$ ；如果 $A_{n-1}+A_{n-2}>A_n$ ，则 $A_n$ 满足条件，可以构造出这样的圆；如果 $A_{n-1}+A_{n-2}\leq A_n$ ，因为 $A_{n-1},A_{n-2}$ 是除了 $A_n$ 以外最大的数，所以把其他任何 $A_i$ 换到 $A_n$ 旁边，都不能使 $A_n$ 两边的数之和大于 $A_n$，此时就不可以构造出这样的圆。

然后这样构造圆，最后检验一下，就可以了。

- 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int n;
long long num[N+5],ans[2*N+5];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%lld",&num[i]);
	sort(num+1,num+1+n);
	int lef=N-1,rig=N+1;
	ans[N]=num[1];
	for(int i=2;i<=n;i++){
		if(i%2) ans[lef--]=num[i];
		else ans[rig++]=num[i];
	}
	for(int i=lef+1;i<rig;i++){
		int A,B;
		if(i==lef+1) A=rig-1,B=i+1;
		if(i==rig-1) A=i-1,B=lef+1;
		if(lef+1<i && i<rig-1) A=i-1,B=i+1;
		if(ans[A]+ans[B]<=ans[i]){
			printf("NO\n");
			return 0;
		}
	}
	printf("YES\n");
	for(int i=lef+1;i<rig;i++)
		printf("%lld%c",ans[i],i==rig-1?'\n':' ');
	return 0;
}

· C题：Candies!

- 题意

对一个长度为 $2^t$ 的数列 $S_0=\{A_1,A_2,A_3,A_4…A_{2^t}\}$，其中 $A_i$ 均为一位正整数，我们对它进行以下操作：

  1. 将 $A_{2i-1}+A_{2i}(1\leq i\leq 2^{t-1})$ 依次放入一个新的数列，即新的数列为：

  2. 计算 $A_1+A_2,A_3+A_3,…,A_{2^t-1}+A_{2^t}$ 中产生了多少次进位，将答案加上产生进位的数量；

  3. 将 $S_1$ 中的每个元素都模 $10$ （也就是取它的个位），作为新的 $S_0$；

    一直进行上述操作，直到 $S_0$ 长度为 $1$。

给出长度为 $n$ 的序列 $S$。$m$ 次询问：每次询问给出 $l,r$，求 $S$ 中 $[l,r]$ 这个子序列进行上述操作得到的答案（保证子序列长度是 $2$ 的幂）

Input 8
8 7 3 1 7 0 9 4
3
1 8
2 5
7 7
Output 3
1
0
Explain 第一次询问区间 $[1,8]$，第一次操作后，得到数列 $\{5,4,7,3\}$，其中 8+7,9+4 产生进位；
第二次操作后，得到数列 $\{9,0\}$，其中 3+7 产生进位；
最后一次操作得到 $\{9\}$，无进位，结束

- 解析

按照题目的意思，我们定义 num[i][j] 表示从 $S$ 的 $[i,i+2^j-1]$ 这个子序列中的所有元素之和的个位；ans[i][j] 表示对 $S$ 的 $[i,i+2^j-1]$ 这个子序列进行操作得到的答案。

显然可以倍增——

  • num[i][j] = ( num[i][j-1] + num[i+(1<<j-1)][j-1] ) % 10 ；
  • 如果 num[i][j-1] + num[i+(1<<j-1)][j-1] 进了位，则 ans[i][j] = ans[i][j-1] + ans[i+(1<<j-1)][j-1] + 1 ；否则就不加最后那个 1。

- 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int n,m;
int num[N+5][20],ans[N+5][20];
int LGLOG2(int num){
	for(int i=0;i<20;i++)
		if((1<<i)==num)
			return i;
}
int main(){
	scanf("%d",&n);
	for(int i=0;i<n;i++) scanf("%d",&num[i][0]);
	for(int siz=1;siz<20;siz++){
		for(int i=0;i<n;i++){
			if(i+(1<<siz)>n) continue;
			int add=num[i][siz-1]+num[i+(1<<siz-1)][siz-1];
			if(add>=10)
				num[i][siz]=add-10,
				ans[i][siz]=ans[i][siz-1]+ans[i+(1<<siz-1)][siz-1]+1;
			else
				num[i][siz]=add,
				ans[i][siz]=ans[i][siz-1]+ans[i+(1<<siz-1)][siz-1];
		}
	}
	scanf("%d",&m);
	while(m--){
		int lef,rig;scanf("%d%d",&lef,&rig);
		int siz=LGLOG2(rig-lef+1);
		printf("%d\n",ans[lef-1][siz]);
	}
	return 0;
}

· D1题：Add on a Tree

- 题意

给出一棵树，一开始每条边的权值都是 $0$；你可以将两个叶子节点之间的简单路径上的所有边的权值都加上一个实数。问经过任意次操作，能否使所有边的权值集合能够取到任意实数。

（不提供样例）

- 解析

其实能够取得任意实数就是说要让任何边的取值都不受限制，换句话说，不存在 任何两条不同的边的取值一定相同。

那么就很好想了，如果一个节点的度数为 2，那么与它相邻的两条边的权值一定相等，也就不满足条件。

所以只需要判断有没有度数为 2 的点就行了。

- 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int n;
int du[N+5];
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int u,v;scanf("%d%d",&u,&v);
		du[u]++;du[v]++;
	}
	for(int i=1;i<=n;i++)
		if(du[i]==2){
			printf("NO\n");
			return 0;
		}
	printf("YES\n");
	return 0;
}

· E题：Count Pairs

- 题意

给出 $n$ 个数 $A_1,A_2,A_3…A_n$ ；再给出 $p,k$ ，询问有多少个数对 $(i,j)$ 满足 $i<j$ 且 $(A_i+A_j)(A_i^2+A_j^2)\equiv k\pmod p$ 。

保证 $p$ 是质数，$0\leq A_i,k<p$ 。

- 解析

将 $(A_i+A_j)(A_i^2+A_j^2)\equiv k\pmod p$ 两边同时乘上 $(A_i-A_j)$；化简：

即数对 $(i,j)$ 只要满足上述条件就可以了。储存 $j$ 之前有多少个 $i$ 满足 $(A_i^4-kA_i)\bmod p=(A_j^4-kA_j)\bmod p$ 。也比较简单——毕竟 C++ 有 map~

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*Lucky_Glass*/
#include<map>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=3e5;
int n;
ll p,k,ans;
ll A[N+3];
map<ll,int> cnt;
int main(){
	scanf("%d%lld%lld",&n,&p,&k);
	for(int i=1;i<=n;i++) scanf("%lld",&A[i]);
	for(int i=1;i<=n;i++){
		ll cur=((A[i]*A[i]%p*A[i]%p*A[i]%p-k*A[i]%p)%p+p)%p;
		ans+=cnt[cur]++;
	}
	printf("%lld\n",ans);
	return 0;
}

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~