OI题解 - Must Be Rectangular! [ABC131 F]

中考完以来打的第一场网络赛

话说什么时候ABC也变成 $6$ 道题而且参与分数线都涨到 $1\text~1999$ 了？题也难了许多，F题感觉还不错，发现了并查集的新用法~

---

· 题意

平面上有 $n$ 个点，给出每个点的坐标——第$i$个点坐标为 $(x_i,y_i)$。

若存在 $3$ 个点 $(x_1,y_1),(x_1,y_2),(x_2,y_1)$ （$x_1\not=x_2且y_1\not=y_2$），则根据这$3$个点在$(x_2,y_2)$ 处新建一个点（如果该位置原本没有点）。这样的$4$个点就围成了一个矩形。

你想要建立尽可能多的点，注意新建立的点也可以和其他点构成新矩形，举个例子：

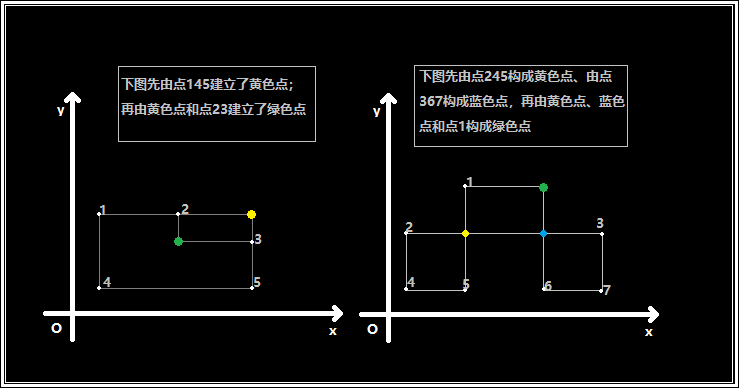
问你最多能够新建多少个点（注意是新建）。

---

· 题解

- 系

我们定义一个“系”，一个系由若干个点构成。点 $(x,y)$ 属于 系$A$ 当且仅当存在点 $(x’,y’)\in A$ 使得 $x’=x或y’=y$（或者 系$A$ 中不包含任何点）。

一个点属于恰好一个系。

然后我们就会发现一个性质：如果我们把系中的所有点的横轴、纵轴都画出来，我们可以得到一个网格，网格的所有交汇点要么是已知的点，要么是可以新建的点，且新建的点仍属于这个系。比如：

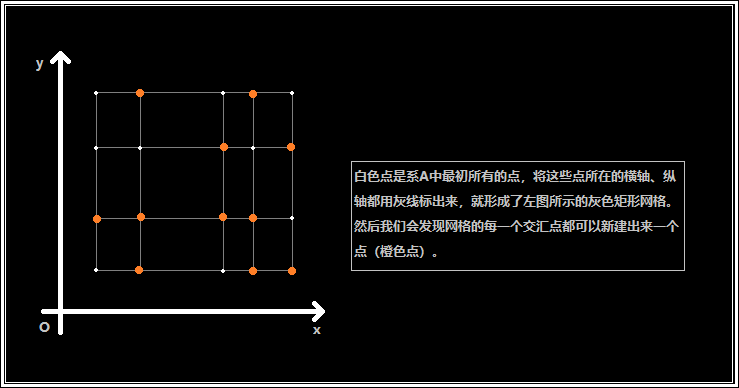
对于一个系，我们定义 $cntx$ 表示系内所有点中不同的横坐标的个数，$cnty$ 表示系内所有点中不同的纵坐标的个数。（比如上图中 $cntx=5,cnty=4$）

则网格中就会出现 $cntx\times cnty$ 个交汇点，也就是上图中橙色点与白色点的个数之和为 $cntx\times cnty$ 。

我们可以发现不同的系中的点不可能构成新建的点。那么如果我们把所有 $n$ 个点划分为 $m$ 个系$\{G_1,G_2,…,G_m\}$，并且令 $S_i$ 表示 $G_i$ 中包含的点的个数、$cntx_i$ 表示系 $G_i$ 内所有点中不同的横坐标的个数、$cnty_i$ 表示系 $G_i$ 内所有点中不同的纵坐标的个数，那么我们能够构造 $\sum_{i=1}^m(cntx_i\times cnty_i)-n$ 个新点。

- 并查集

现在我们需要求出上述的系，于是可以想到用一个并查集储存一个系。

但是这个并查集里面储存的并不是系里的点，而是系里的点的 横、纵坐标——因为一个点可以用横坐标和纵坐标表示，而且根据之前的结论，一个系里所有能够新建出来的点和原本的点的总个数是 $cntx\times cnty$ —— 如果我们将横、纵坐标储存在一个并查集里，我们可以迅速算出 $cntx$ 和 $cnty$ ，从而得到解。

具体实现见代码。

---

· 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5;
int n;
int pre[2*N+5],cntX[2*N+5],cntY[2*N+5];
int Find(int u){return pre[u]=(pre[u]==u? u:Find(pre[u]));}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=2*N;i++) pre[i]=i;
	for(int i=1;i<=n;i++){
		int x,y;scanf("%d%d",&x,&y);
		int Fx=Find(x),Fy=Find(N+y);
		if(Fx!=Fy) pre[Fx]=Fy;
	}
	for(int i=1;i<=2*N;i++){
		int Fi=Find(i);
		if(i<=N) cntY[Fi]++;
		else cntX[Fi]++;
	}
	ll ans=0;
	for(int i=1;i<=2*N;i++)
		ans+=1ll*cntX[i]*cntY[i];
	printf("%lld\n",ans-n);
	return 0;
}

---

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~