OI题解 - Burza [COCI 2016/2017 Round 2]

这场比赛真的不错~

这应该是第六题也就是最后一题。

---

· 题目

有一棵$n$个节点的树，树的 节点$1$ 上有一枚硬币。Daniel 和 Stjepan 用这棵树玩游戏。游戏的过程如下：

1. Daniel 选择一个节点并把它标记；
2. Stjepan 将硬币移动到与硬币所在节点$u$相连的未标记的节点$v$，并标记节点$u$；
3. 一直循环1,2步骤，直到Stjepan将进行2步骤时无法移动硬币。

Daniel 想要尽快结束游戏（也就是让Stjepan移动硬币的次数尽可能小），而Stjepan想要尽可能多地移动硬币。为了增加游戏难度，Daniel 决定不看 Stjepan 将硬币移动到哪个位置（也就是说 Daniel 标记节点时并不知道此时硬币在哪），但是 Daniel 知道这棵树长什么样子。

Daniel 希望硬币移动的次数 小于 $m$ 次。请问是否存在 Daniel 标记节点的方案，使得 Stjepan 无论如何移动硬币，都不能移动硬币 $m$ 次。存在输出 “DA”，否则输出“NE”。

数据规模：

$1\leq m\leq n\leq 400$

---

· 解析

- 初步分析

我们将节点$1$作为树的根，并把节点$1$的深度设为$0$，不难发现 Stjepan 第 $i$ 次移动硬币后，硬币会在深度为 $i$ 的某一个节点上。那么问题就变成“是否存在Deniel标记节点的方案，使得Stjepan无论怎么移动硬币都不能使硬币到达深度为$m$的节点”。

只要硬币到达深度为 $m$ 的节点，这个标记方案就“失败”了。可见深度大于$m$的节点是没有意义的。
所以我们称深度恰好为 $m$ 的节点为“叶节点”。

请看下面两种情况，硬币在节点$U$，此时Daniel标记节点：

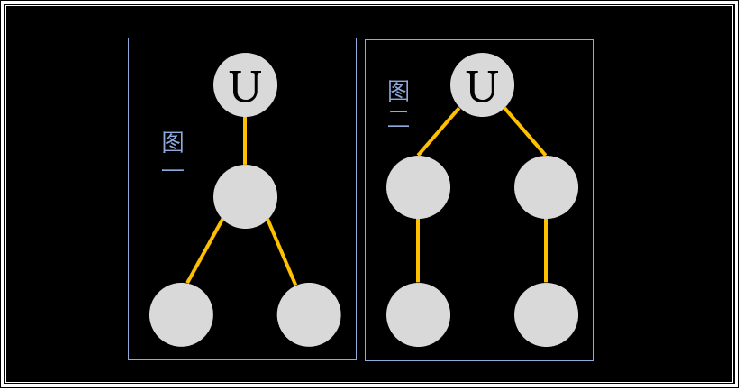
贪心地想——为了使硬币走的步数尽可能少，显然图一的情况更容易。为什么呢？

我们定义 $cnt_i$ 表示以节点 $i$ 为根的子树中“叶节点”的个数。假设上图的图一、图二中第$3$层的点都是“叶节点”，那么图一中 节点$U$ 的子节点的 $cnt$ 为 $2$ ，而图二中 节点$U$ 的两个子节点的 $cnt$ 都为 $1$。

仍然是贪心的思想，我们标记 $cnt$ 大的点一定更“合算”，因为 $cnt$ 越大，能够“堵住”的叶节点就越多。

根据这一点，我们可以构造出一个最坏情况的图：

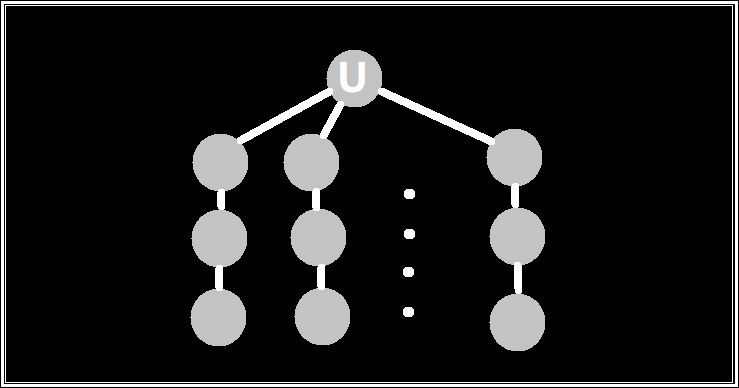
这个图“坏”在除了根节点$U$，其他所有点的 $cnt$ 都是 $1$，这意味着我们标记一个点只能堵住一个叶节点。对于这种图，我们怎么完成方案呢？

可以发现当硬币的深度为 $i$ 时，我们一定会标记深度为 $i+1$ 的点。而且相同深度的点我们只会标记一个。

假设叶节点的个数是 $t$，我们就需要标记 $t$ 个点才能将所有叶节点堵完。则当 $m\ge t$ 时，我们就可以把所有叶节点堵完，就输出 $DA$。

这是最坏情况，需要满足 $t\leq m$ ，那么对于其他情况，如果 $t\leq m$ ，也一定可以找到解。而我们知道，对于最坏情况，$t\leq \frac nm$ —— 如果 $\frac nm\leq m$ ，即 $n\leq m^2$，那 $t$ 就一定小于等于 $m$，此时一定存在解，如果最坏情况情况都有解，那其他情况都有解。

于是分成两种情况：

1. $n\leq m^2$ 此时直接输出 “DA”；（证明看上面）
2. $n>m^2$

- 处理 $n>m^2$ 的情况

因为 $n\leq 400$ ，那此时 $m<20$ 即 $m\leq 19$ 。

也就是说叶节点的深度不超过 $19$ ……又因为根据之前的分析，同一个深度的节点我们最多会标记一个……en……状态压缩？（Right!）
对于二进制数 $S$ ，如果 $S$ 的第 $i$ 位为 $1$ ，就说明标记了一个深度为$i$的节点。

对于每个叶节点，我们将它们从左到右编号（这样能够保证一棵子树里包含的叶节点的编号是连续的），并且定义 lev[u][0] 表示以 $u$ 为根节点的子树中的叶节点的最小编号，lev[u][1] 表示以 $u$ 为根节点的子树中的叶节点的最大编号。因为以 $u$ 为根节点的子树中叶节点的编号是连续的 ，那么该子树中包含的叶节点为 lev[u][0]~lev[u][1] 。

定义数组 rig[i] 储存 lev[u][1]==i 的所有 u。

定义 dp[i][S] 表示能否通过标记 $S$ 深度的点堵住前 $i$ 个叶节点。

显然：最初状态为 dp[0][0]=true ，状态转移方程式为：

u=rig[i][t]
dp[i][S]|=dp[lev[u][0]-1][S^(1<<dep[u])]
//dep[u]表示u的深度
//保证 (1<<dep[u])&S == 0

最后判断 (cntlev是叶节点个数) dp[cntlev] 中有没有 S 满足 dp[cntlev][S]==true 就好了~

---

· 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=400,INF=(1<<29);
int n,m,cntlev;
vector<int> lnk[N+5],rig[N+5];
int dep[N+5],lev[N+5][2];
bool dp[N+5][(1<<19)+5];
void DFS(int u,int pre) {
  dep[u]=dep[pre]+1;
  if(dep[u]==m-1) {
    lev[u][0]=lev[u][1]=++cntlev;
    return;
  }
  for(int i=0; i<(int)lnk[u].size(); i++) {
    int v=lnk[u][i];
    if(v==pre) continue;
    DFS(v,u);
    lev[u][0]=min(lev[u][0],lev[v][0]);
    lev[u][1]=max(lev[u][1],lev[v][1]);
  }
}
int main() {
  freopen("burza.in","r",stdin);
  freopen("burza.out","w",stdout);
  scanf("%d%d",&n,&m);
  for(int i=1; i<n; i++) {
    int u,v;
    scanf("%d%d",&u,&v);
    lnk[u].push_back(v);
    lnk[v].push_back(u);
  }
  if(m*m>=n) {
    printf("DA\n");
    return 0;
  }
  for(int i=1; i<=n; i++) lev[i][0]=INF,lev[i][1]=-INF;
  dep[0]=-2;
  DFS(1,0);
  for(int i=2; i<=n; i++)
    if(lev[i][0]!=INF)
      rig[lev[i][1]].push_back(i);
  dp[0][0]=true;
  for(int pos=1; pos<=cntlev; pos++)
    for(int S=0; S<(1<<m); S++) {
      for(int i=0; i<(int)rig[pos].size(); i++) {
        int u=rig[pos][i];
        if((1<<dep[u])&S)
          dp[pos][S]|=dp[lev[u][0]-1][S^(1<<dep[u])];
      }
    }
  for(int i=0; i<(1<<m); i++)
    if(dp[cntlev][i]) {
      printf("DA\n");
      return 0;
    }
  printf("NE\n");
  return 0;
}

---

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~