减少边的思路挺巧妙的……只是……BZOJ你为什么不更新题面啊(数据规模BZOJ上写的 $n\le3000$,实际上是 $n\le5000$)
Part1. 题面
Part1/1. 描述
某学校的每个建筑都有一个独特的编号。
一天你在校园里无聊,决定在校园内随意地漫步。你已经在校园里呆过一段时间,对校园内每个建筑的编号非常熟悉,于是你情不自禁的把周围每个建筑的编号都记了下来——但其实你没有真的记下来,而是把每个建筑的编号除以 $2$ 取余数得到 $0$ 或 $1$,作为该建筑的标记,多个建筑物的标记连在一起形成一个 01串。
你对这个串很感兴趣,尤其是对于这个串是回文串的情况,于是你决定研究这个问题。学校可以看成一张图,建筑是图中的顶点,而某些顶点之间存在无向边。对于每个顶点我们有一个标记( $0$ 或者 $1$ )。
每次你会选择图中两个顶点,你想知道这两个顶点之间是否存在一条路径使得路上经过的点的标记形成一个回文串。
一个回文串是一个字符串使得它逆序之后形成的字符串和它自己相同,比如 010,1001 都是回文串,而 01,110 不是。注意长度为1的串总是回文串,因此如果询问的两个顶点相同,这样的路径总是存在。
此外注意,经过的路径不一定为简单路径,也就是说每条边每个顶点都可以经过任意多次。
Part1/2. 输入
第一行三个整数 $n,m,q$,表示图中的顶点数和边数,以及询问数。
第二行为一个长度为 $n$ 的 01串,其中第 $i$ 个字符表示第 $i$ 个顶点(即顶点 $i$)的标记,点从 $1$ 开始编号。
接下来 $m$ 行,每一行是两个整数 $u_i,v_i$,表示顶点 $u_i$ 和顶点 $v_i$ 之间有一条无向边,不存在自环或者重边。接下来 $q$ 行,每一行存在两个整数 $x_i,y_i$,表示询问顶点 $x_i$ 和顶点 $y_i$ 的点之间是否有一条满足条件的路径。
Part1/3. 输出
输出 $q$ 行,每行一个字符串 YES,或者 NO(引号不输出)。输出 YES 表示满足条件的路径存在,输出 NO 表示不存在。
Part1/4. 数据规模
$1\le n\le5000$,$1\le m\le500000$,$1\le q\le100000$;
Part2. 解析
> Tab.
下面把标记为 1 的点称为“黑色”,标记为 0 的点称为“白色”
题面很长,但是非常友好地把关键点都标记了。
很容易想到先处理出所有答案,再 $O(1)$ 回答询问(毕竟 $q$ 的规模太大了)。
然后就得到了一个 30pt 的思路 —— 从已经判断出“能够找到从 $u$ 到 $v$ 的一条回文路径”的点对 $(u,v)$ 向外扩展 —— 即找到与 $u$ 相邻的点 $x$、与 $v$ 相邻的点 $y$,如果 $x,y$ 的颜色相同,那么 $(x,y)$ 也一定是满足条件的点对。
我们发现这样的点对的数量是 $O(n^2)$ 的(每个点对都可以是满足条件的,比如所有点颜色相同),而枚举分别与 $u,v$ 相邻的点 $x,y$ 又要花费 $O(n^2)$ 的复杂度,这样总复杂度变成了 $O(n^4)$,显然是会 TLE 的……
> Tab.
比如给出的图是一个完全图,那么枚举 $x,y$ 就是 $O(n^2)$ 的复杂度了
点对数量 $n^2$ 已经无法优化,考虑优化相邻的点——断掉一些边,使得原来能够找到回文路径的点对仍然能够找到回文路径。
注意到题目中强调了 “不一定是简单路径”,那么可以重复地一直走某一条颜色相同的边,表现在路径上,就是增加了偶数 个连续的同种颜色。这意味着 —— 只要两段连续相同颜色的数量的 奇偶性 相同,就一定可以使这两段的数量也相同。
> Example
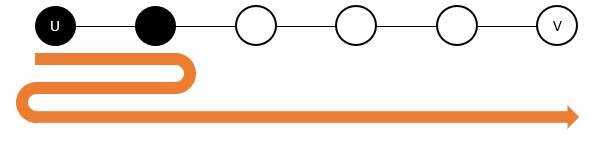
虽然黑色点和白色点数量不等,但是数量的奇偶性相同,可以通过(上图所示)重复走颜色相同的边,使得两种颜色数量也相等。
考虑什么时候颜色数量的奇偶性会变化,发现只有经过一个 奇环 的时候。
于是考虑把边分成两类,第一类边连接颜色相同的点,第二类边连接颜色不同的点。分别考虑两类边构成的子图 $G,H$ ,$G$ 中只有第一类边,$H$ 中只有第二类边。
对于 $G$ 中的每个连通块,要删去一些边,使它仍然连通;又因为奇环能够改变颜色数量的奇偶性,如果连通块中有奇环,就保留一个奇环(多余的奇环也没有必要保留),那就是要生成一棵带奇环的基环树 嘛!DFS 一遍就好了。
对于 $H$ 中的每个连通块,不难发现它一定是个二分图,所以不存在奇环。只要保证连通性就好了,直接生成一棵树即可。
因为基环树和树的边的数量都是 $O(n)$ 的,所以就可以将最初的暴力的均摊复杂度降到 $O(n^2)$ 就可以过了!
Part3. 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
|
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=5000,M=5e5;
#define fir first
#define sec second
struct NODE{
int to;NODE *nxt;
NODE(){}
NODE(int _t,NODE *_n):to(_t),nxt(_n){}
};
struct GRAPH{
NODE pol[M*2+3],*ncnt,*had[N+3];
GRAPH(){ncnt=pol;}
void AddEdge(int u,int v){
NODE *p=++ncnt,*q=++ncnt;
*p=NODE(v,had[u]);had[u]=p;
*q=NODE(u,had[v]);had[v]=q;
}
NODE* operator [](int id){return had[id];}
}Gsam,Gdif,Gr;
struct EDGE{
int u,v;
EDGE(){}
EDGE(int _u,int _v):u(_u),v(_v){}
}Ed[M+3];
int n,m,q;
int col[N+3];
bool ans[N+3][N+3],cir;
char id[N+10];
queue< pair<int,int> > que;
void BFS(int x,int y){
if(ans[x][y] || id[x]!=id[y]) return;
ans[x][y]=ans[y][x]=true;
que.push(make_pair(x,y));
while(!que.empty()){
int ux=que.front().fir,uy=que.front().sec;
que.pop();
for(NODE *itx=Gr[ux];itx;itx=itx->nxt)
for(NODE *ity=Gr[uy];ity;ity=ity->nxt){
int vx=itx->to,vy=ity->to;
if(ans[vx][vy] || id[vx]!=id[vy]) continue;
ans[vx][vy]=ans[vy][vx]=true;
que.push(make_pair(vx,vy));
}
}
}
void DFSSAM(int u,int cl){
col[u]=cl;
for(NODE *it=Gsam[u];it;it=it->nxt){
int v=it->to;
if(col[v]!=-1){
if(col[v]==col[u] && !cir){
cir=true;
Gr.AddEdge(u,v);
}
}
else{
Gr.AddEdge(u,v);
DFSSAM(v,!cl);
}
}
}
void DFSDIF(int u){
col[u]=1;
for(NODE *it=Gdif[u];it;it=it->nxt){
int v=it->to;
if(col[v]!=-1) continue;
Gr.AddEdge(u,v);
DFSDIF(v);
}
}
int main(){
scanf("%d%d%d\n",&n,&m,&q);
scanf("%s",id+1);
for(int i=1;i<=m;i++){
int u,v;scanf("%d%d",&u,&v);
Ed[i]=EDGE(u,v);
if(id[u]==id[v]) Gsam.AddEdge(u,v);
else Gdif.AddEdge(u,v);
}
memset(col,-1,sizeof col);
for(int i=1;i<=n;i++)
if(col[i]==-1){
cir=false;
DFSSAM(i,1);
}
memset(col,-1,sizeof col);
for(int i=1;i<=n;i++)
if(col[i]==-1)
DFSDIF(i);
for(int i=1;i<=n;i++)
BFS(i,i);
for(int i=1;i<=m;i++)
BFS(Ed[i].u,Ed[i].v);
while(q--){
int u,v;scanf("%d%d",&u,&v);
if(ans[u][v]) printf("YES\n");
else printf("NO\n");
}
return 0;
}
|
The End
Thanks for reading!
评论功能也许后期会加入吧……(gu)
