前行 - CSP2019全国排位 Day1 | Lucky_Glass's Blog

以心为名，名为爱惜

0%

前行 - CSP2019全国排位 Day1

发表于 分类于 Valine：

两道题想到正解然后都写炸了 不知道在干什么

Part1. 总结（不重要）

这几天的状态不算特别好（从打 AGC 打爆开始），后面的几场 OI 制的模拟赛都不是特别顺畅。还有一种以前的“习惯写不出正解”的奇怪心态。

这次 noi.ac 的模拟赛其实不算难 —— 赛后，前两道题修修补补就过了，第三题的正解也非常好理解，基本上赛后不到一个小时就把这些题补完了。总的说来，这次体现出来的主要缺漏有两个：

  1. 不会分析时间复杂度
  2. 不会推导数学性质（这是硬伤）
  3. （其实还有一小点别的）

第一点体现在 T2，其实考试时就想到了正解，然后误判成了一个 $O(n^2)$ 的算法，以为只是一个部分分，数组只开了部分分的范围……

第二点就是 T3，根本就没有往正解的 $\sum a_i\le a_t+b_t$ 这个式子去想。

Part2. 题面

T1. 序列

有一种生成数列的方式：

给定参数 $k,A=(a_0,a_1,\dots,a_k)$ ，生成一个无限长的数列，其中第 $i$ 项为 $\sum_{j=0}^ka_ji^j$

现给出 $m$ 组 $k_i,A_i=(a_{i,0},a_{i,1},\dots,a_{i,k})$ ，按上面的规则生成 $m$ 个无限长的序列。然后把这 $m$ 个序列合并起来再从小到大排序，求得到的新序列的第 $n$ 项。

保证答案不超过 $10^{18}$。

数据规模：$1\le n\le10^5$，$1\le m\le3\times10^4$，$1\le k\le7$，$0\le a_i\le1000$。

T2. 积木

一块积木长为 2 高为 1，用这样的积木搭起一面无限高、无限宽的墙，并定义坐标系（每块积木的左边部分的横纵坐标奇偶性相同），如下图：

png1

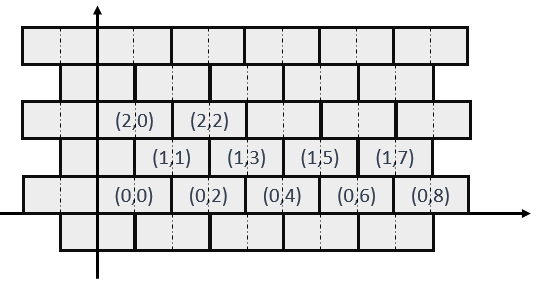
现在抽出 n 个积木，第 i 块积木是 $(x_i,y_i)$，保证 $x_i$ 和 $y_i$ 奇偶性相同。当 $(x-1,y-1)$ 和 $(x-1,y+1)$ 两块积木都消失时，积木 $(x,y)$ 会塌落（塌落后就消失）。

问抽出这 $n$ 个积木后，总共会掉落多少个积木（包括抽出的 $n$ 块积木）。

数据规模：$1\le n\le3\times10^5$，$-10^9\le x_i,y_i\le10^9$。保证 $x_i,y_i$ 奇偶性相同且抽出的 $n$ 个积木不相同。

T3. 保镖

一共有 n 个保镖等待聘用，第 i 个保镖可以连续工作 $a_i$ 个小时，接下来的 $b_i$ 个小时他必须休息。而且对于每一个保镖 i，他工作完成后，只有当聘用的其他所有保镖都工作了，他才会继续工作。

你需要聘用尽可能少的保镖，使得在任何时刻都有保镖工作。求最少需要聘用多少保镖；如果无法满足“任何时刻都有保镖工作”，输出 -1。

数据规模：$1\le n\le5\times10^5$，$1\le a_i,b_i\le10^{12}$。

Part3. 个人细节（不重要）

T1. 序列

其实这道题一开始卡了很久，没记错的话应该是把 $k$ 看成 $m$ 了，误以为计算一次序列的第 $i$ 项会有 $O(m)$ 的复杂度（这样的话总复杂度应该是 $O(nm\log_2 m)$），然后之后很久才注意到计算应该是 $O(k)$ 的，然后就这样写了。

考虑到虽然答案不会超过 long long，但是计算过程中，得到的不是答案的数可能是超过 long long 的，就处理了一下计算乘法和加法时的数字大小……结果有个地方把变量名写错了，导致有一些不会爆 long long 的计算误判成会爆……（最后听说这道题也没有卡 long long 来着）

T2. 积木

推导了很久的性质，最后自己推导出来一个“碗”状的东西，但是没法维护……就放弃了，开始打部分分。

一开始做的是 $1\le x_i,y_i\le5000$ 的部分分，写的复杂度是 $O(5000^2)$，就是从最底下暴力判断每一层哪些积木会掉落。然后感觉 20pt 太少了，说不过去……然后就想要做 40pt 的第 1,2 个部分分。

想到 $1\le x_i,y_i\le5000$ 的计算方法中其实有很多层不会有抽出去的积木，因此可以预先知道是哪些积木掉下来。于是就初步精简成了 $O(n^2)$ ，又结合了之前推导的所谓”碗“形，想到了可以用链表维护（还可以用堆维护，当时没有想到）。

实际上，我那个算法的复杂度应该是常数较大的 $O(n)$……（后面再讲为什么是 $O(n)$ ）但是我以为是 $O(n^2)$ ，链表就只开了部分分的规模。虽然还有一些细节写错了，赛后修修补补就 AC 了 QwQ

T3. 保镖

受 C题 影响(？？) 以为这道题很难，再加上自己推导了一下，感觉没什么结果。然后就没什么思路。

Part4. 题解

T1. 序列

注意到 $k\le7$，所以计算某一个序列的第 $i$ 项的复杂度简直可以当作常数处理。而且还有一个非常显然的性质 —— 这 m 个序列，每个都是 单调递增 的。

因此可以贪心 —— 用堆（优先队列）维护当前最小的数。每次取出最小的数（堆顶），然后把它换成它所在的序列的下一个数，再塞进堆里……取出来的第 n 个数就是答案。

这样的话，堆里的元素始终只有 m 个，所以复杂度稳定 $O(\log_2m)$ ；取出 n 次；计算复杂度 $O(k)$；总共是 $O(nk\log_2m)$，可以接受。

小插曲：关于判断是否超过 $10^{18}$。

其实确实是可以判断的，而且我觉得应该要判断……不知道为什么不判断可以 AC……（因为我觉得当我们取出堆顶后，它的下一个数可能会变得很大，虽然堆顶在 $10^{18}$ 以内，但是下一个数可能会超过 $10^{18}$。它一定不会是答案，但是如果它爆了 long long 变成负数，就到堆顶去了。）

对于计算 $a\times b$ ，$a,b$ 都没有爆 long long，如果 $a\times b>10^{18}$，则 $a>\left\lfloor\frac {10^{18}}b\right\rfloor$；这样就可以判断了。

计算 $a+b$，如果 $a>10^{18}-b$ 就爆了。

T2. 积木

不难发现，如果只考虑抽出同一行的连续 k 块积木，会有 $\frac{(k+1)k}2$ 块积木消失，比如这样（抽出橙色积木，黄色积木也会消失）：

png2

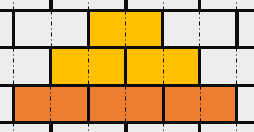
而且设抽出的积木是 $(x,y),(x,y+2),\cdots,(x,y+2k-2)$ 这 k 块连续的积木，第 $x+i$ 层（$i< k$）会掉落 $(x+i,y+i),(x+i,y+i+2),\cdots,(x+i,y+2k-2-i)$ 这 $k-i$ 块积木。

只要第 i 行没有抽出其他的积木，我们就 可以直接知道 第 i 行的消失情况。

因此我们只需要处理有积木被抽出的行 —— 用链表维护第 i 行有 哪几段积木 消失了，从第 i 层转移到第 j 层（$i<j$）就是下面这样的过程：

png3

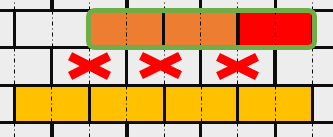
j=i+2 的情况（红色是第 j 层要抽出的积木）：

黄色段是第 i 层会消失的段。第 i+1 层没有抽出积木，因此我们可以直接计算出打了叉的这些积木会消失。还可以计算出第 j 层的橙色积木也会消失。橙色段与要抽出的红色积木连成了连续的一段区间，因此把它们合并成一段继续计算。

假如 j 离 i 太远，黄色段不会对第 j 层的积木造成影响，就直接计算出黄色段会造成多少个积木消失，然后删掉这一段。

假如第 j 层删除的积木没有与橙色段相连，就新建长度为 1 的一段新区间，然后按 从左到右 的顺序插入到链表里。

要处理元素（区间）的修改（合并）、依次访问、任意位置插入以及删除，链表还是非常好用的，尤其是手写链表的优势就非常明显。

关于时间复杂度：

由于只有额外抽出的 n 个积木可能会造成新建一个段。所以链表中维护的段最多只有 n 个，而每个段只会被删除一次（如果一个要抽出的积木合并到另一个段里了，视为这个要抽出的积木新建的段被删除），因此复杂度是 $O(n)$，但是由于有一些遍历的复杂度，会有较大的常数。但是还好不会卡常……

T3. 保镖

不妨把每个保镖的工作看成一个长度为 $a_i+b_i$ 的循环，在这段循环中，每个时刻都必须有人工作。那么如果我们选的保镖中 t 的 $a_t+b_t$ 最大，那么选的这些保镖的 $a_i$ 必须要能够 填满 这个 $a_t+b_t$。

可能表现成线段图更直观：

png4

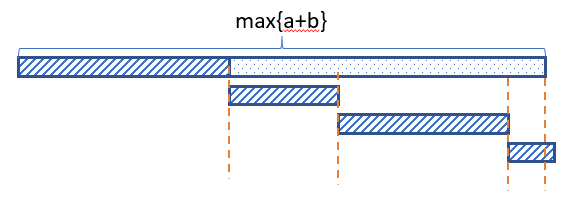
（斜线段表示保镖工作的段 $a_i$）

这样的一个安排就是合法的，因为每个保镖的 $a_i+b_i\le\max\{a_i+b_i\}$ ，所以在这样一个长度 $\ge\max\{a_i+b_i\}$ 的循环中，每个保镖都会在他开始工作之前完成休息。

那么可以考虑 先确定 $\max\{a_i,b_i\}=t$ ，再用 $a_i+b_i\le t$ 的保镖的 $a_i$ 来填满 $t$ 。显然贪心地想，要取尽可能大的 $a_i$ 才能使聘用的保镖尽可能少。

根据这个思路 —— 我们可以先把所有保镖按 $a_i+b_i$ 从小到大排序，然后从小到大枚举 $t=a_i+b_i$，同时用 权值线段树 维护小于等于 $t$ 的 $a_i+b_i$ 的每个 $a_i$ 的数量（当然要离散化），然后在线段树上查询尽可能取大的 $a_i$，至少要取多少个才能使它们的和大于等于 $t$，比较像平衡树的查询，具体可见代码 。对于每个 $t$ 都 $O(\log_2 n)$ 的复杂度查询一下，取最小值即可。

Part5. 源代码

T1. 序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/*Lucky_Glass*/
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int M=3e4,K=7;

int n,m,k;
int cA[M+3][K+3];
struct QNODE{
	long long num;int id,pos;
	QNODE(){}
	QNODE(long long _n,int _i,int _p):num(_n),id(_i),pos(_p){}
};
bool operator <(QNODE A,QNODE B){return A.num>B.num;}
priority_queue< QNODE > que;

int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=m;i++){
		int tot=0;
		for(int j=0;j<=k;j++){
			scanf("%d",&cA[i][j]);
			tot+=cA[i][j];
		}
		que.push(QNODE(1ll*tot,i,1));
	}
	QNODE now;
	const long long INF=(long long)(1e18);
	for(int i=1;i<=n;i++){
		now=que.top();que.pop();
		int id=now.id,nxt=now.pos+1;
		QNODE cop(0,id,nxt);
		long long val=1;
		bool Bb=false,Bc=true;
		for(int j=0;j<=k;j++){
			if(cA[id][j] && Bb) Bc=false;
			if(cop.num>INF-val*cA[id][j]) Bc=false; //这里在判 1e18
			cop.num+=val*cA[id][j];
			if(val>INF/nxt) Bb=true; //这里也在判 1e18
			val*=nxt;
		}
		if(Bc) que.push(cop);
	}
	printf("%lld\n",now.num);
	return 0;
}

T2. 积木

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
/*Lucky_Glass*/
#include<stack>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=3e5;
#define fir first
#define sec second

int n;
struct POSI{
	int x,y;
	POSI(){}
	POSI(int _x,int _y):x(_x),y(_y){}
	int& operator [](int id){return id? y:x;}
}del[N+3];

bool cmpPOSI(const POSI &a,const POSI &b){return a.x!=b.x? a.x<b.x:a.y<b.y;}
struct TNODE{TNODE *lef,*rig;int cell,celr;};
struct TLIST{
	TNODE pol[N+3],*head,*tail;stack<TNODE*> abl;
	TNODE *NewNode(int l,int r){
		TNODE *resu=abl.top();abl.pop();
		resu->lef=resu->rig=NULL;
		resu->cell=l;resu->celr=r;
		return resu;
	}
	void Init(){
		for(int i=0;i<=N;i++) abl.push(pol+i);
		head=NewNode(-2e9,-2e9);
		tail=NewNode(2e9,2e9);
		head->rig=tail;tail->lef=head;
	}
	void Delete(TNODE *it){
		abl.push(it);
		it->lef->rig=it->rig;
		it->rig->lef=it->lef;
	}
}Llist;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d%d",&del[i][0],&del[i][1]);
	
	sort(del+1,del+1+n,cmpPOSI); //先按 x 小，再按 y 小
	
	Llist.Init(); //手写链表的初始化，带有哨兵节点 head,tail
	long long ans=0;
	for(int i=1;i<=n;){
		int cel=del[i].x;
		TNODE *it=Llist.head;
		while(i<=n && del[i].x==cel){
			while(it && it->cell<del[i].y) it=it->rig;
            //如果要抽出的积木不是本身就要掉落的积木
			if(it->lef->celr<del[i].y && del[i].y<it->cell){
				TNODE *p=Llist.NewNode(del[i].y,del[i].y);
				p->lef=it->lef;p->rig=it;
				p->lef->rig=p->rig->lef=p;
			}
			i++;
		}
		it=Llist.head->rig;
		while(it!=Llist.tail){
            //如果可以向左边合并
			if(it->lef->celr+2==it->cell){
				it->lef->celr=it->celr;
				Llist.Delete(it);
			}
			it=it->rig;
		}
		it=Llist.tail->lef;
		while(it!=Llist.head){
			//如果可以向右边合并
            if(it->rig->cell==it->celr+2){
				it->rig->cell=it->cell;
				Llist.Delete(it);
			}
			it=it->lef;
		}
		it=Llist.head->rig;
		int maxhg=del[i].x-cel;
        //计算每一段的影响以及下一层的段
		while(it!=Llist.tail){
			int len=(it->celr-it->cell)/2+1;
			if(len<=maxhg || i>n){ //对下一层没有影响（注意顶层）
				ans+=(len+1ll)*len/2;
				Llist.Delete(it);
			}
			else{ //有影响
				ans+=(len-maxhg+1ll+len)*maxhg/2;
				it->cell+=maxhg;it->celr-=maxhg;
                //更新为下一层的段
			}
			it=it->rig;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

T3. 保镖

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/*Lucky_Glass*/
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=5e5;

int n;
vector<long long> uni;
struct NODE{long long a,b;}nod[N+3];

struct SEGTREE{
	long long sum[N<<2];
	int cnt[N<<2];
	void PushUp(int u){
		sum[u]=sum[u<<1]+sum[u<<1|1];
		cnt[u]=cnt[u<<1]+cnt[u<<1|1];
	}
	void Modify(int u,int Cl,int Cr,int Dv){
		if(Dv<Cl || Cr<Dv) return;
		if(Cl==Cr){
			sum[u]+=uni[Dv];
			cnt[u]++;
			return;
		}
		int Cm=(Cl+Cr)>>1;
		Modify(u<<1,Cl,Cm,Dv);
		Modify(u<<1|1,Cm+1,Cr,Dv);
		PushUp(u);
	}
	int Query(int u,int Cl,int Cr,long long Dv){
		if(Cl==Cr) return Dv/uni[Cl]+(bool)(Dv%uni[Cl]);
		int Cm=(Cl+Cr)>>1;
		if(sum[u<<1|1]>=Dv) return Query(u<<1|1,Cm+1,Cr,Dv);
		else return Query(u<<1,Cl,Cm,Dv-sum[u<<1|1])+cnt[u<<1|1];
	}
}Stre;

bool cmpNODE(const NODE &A,const NODE &B){return A.a+A.b<B.a+B.b;}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld",&nod[i].a,&nod[i].b);
		uni.push_back(nod[i].a);
	}
	uni.push_back(-1);
	sort(uni.begin(),uni.end());
	uni.erase(unique(uni.begin(),uni.end()),uni.end());
	sort(nod+1,nod+1+n,cmpNODE);
	int Ssiz=uni.size()-1;
	int ans=n+1;
    //按 a+b 从小到大插入到权值线段树里，自然就得到需要的权值线段树
	for(int i=1;i<=n;i++){
		int id=lower_bound(uni.begin(),uni.end(),nod[i].a)-uni.begin(); //离散化
		Stre.Modify(1,1,Ssiz,id);
		if(Stre.sum[1]>=nod[i].a+nod[i].b)
			ans=min(ans,Stre.Query(1,1,Ssiz,nod[i].a+nod[i].b));
	}
	if(ans==n+1) printf("-1\n");
	else printf("%d\n",ans);
	return 0;
}

The End

Thanks for reading！