前行 - NOIP模拟赛(2019/3/16)

信竞周考？
不过题的质量还是不错（全场一个上100分的都没有……）

---

· A题：星际旅行(tour.cpp)

- 题目

$n$ 个星球之间有 $m$ 条双向道路连接。你需要规划一条旅行路线，满足下列要求：

• 你可以从任意一个星球出发，在任意一个星球结束旅行；
• 可以重复经过同一个星球；
• 在路线中有恰好 $2$ 条道路只经过一次，其余 $(m-2)$ 条道路恰好经过两次；

求你能够找到多少条不同的路线。两条路线不同当且仅当至少有一条道路在两条路线中经过的次数不同。

Tab. $1 \leq n,m \leq 10^5$ ，可能存在自环，但不同点之间最多只有一条边

- 解析

根据题意可知，如果我们把每条边都复制一份（比如原图中1,3之间有一条边，复制后1,3之间就有两条边），然后删除其中的两条边（不是同一条边复制出来的），剩下的图形能够一笔画，这样就是可以的。

而一笔画就可以联系到欧拉路 —— 只要删去两条边后度数为奇数的点（后简称“奇数点”，及“偶数点”）的个数不超过 $2$ 个且图连通（这一点必须注意，图联通指的是从一条边出发能够经过所有的边，而非从一个点出发能够到达所有的点）！

由于所有边都被复制了，删边前所有点都应该是偶数点。有几种删除两条边的方法可以使奇数点的个数不超过 $2$ ？
① 两条有相同端点 $u$ 的边$(u,a),(u,b)$：$u$ 仍为偶数点，$a,b$ 变为奇数点，恰好两个；
② 一个自环$(u,u)$和任意边$(a,b)$：删去自环后 $u$ 仍为偶数点，再删去任意边后 $a,b$ 变为奇数点，恰好两个；
③ 两个自环$(u,u),(v,v)$：显然 $u,v$ 都是偶数点；

至于判断连通，可以用并查集也可以DFS。我这里用并查集，需要判断如果两点不在一个并查集内（即不连通），且两点都有连接的边（包括自环），此时才判断无解。

- 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5;
int du[N+3],cir;
int fa[N+3],edg[N+3][2];
int Find(int u){return fa[u]=(fa[u]==u? u:Find(fa[u]));}
int main(){
	freopen("tour.in","r",stdin);
	freopen("tour.out","w",stdout);
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) fa[i]=i;
	for(int i=1;i<=m;i++){
		int u,v;scanf("%d%d",&u,&v);
		edg[i][0]=u;edg[i][1]=v;
		if(Find(u)!=Find(v))
			fa[fa[v]]=fa[u];
		if(u!=v) du[u]++,du[v]++;
		else cir++;
	}
	int pnt=Find(edg[1][1]);
	for(int i=2;i<=m;i++)
		if(pnt!=Find(edg[i][1])){
			printf("%d\n",0);
			return 0;
		}
	long long ans=0;
	for(int i=1;i<=n;i++)
		ans+=(du[i]-1ll)*1ll*du[i]/2;
	ans+=1ll*cir*(cir-1ll)/2;
	ans+=1ll*cir*(m-cir);
	printf("%lld\n",ans);
	return 0;
}

---

· B题：砍树(cut.cpp)

- 题目

你种了 $n$ 棵树，树的高度一开始都是 $0$ 。每过一天树会长高 $1$ ，对于第 $i$ 棵树，你希望它的高度恰好为 $a_i$ 。

你决定每隔 $d$ 天（也就是在第 $kd(k为正整数)$ 天）检查一次，如果在检查时发现第 $i$ 棵树的高度 $h_i$ 大于等于 $a_i$ ，你会砍掉它高出的部分 $h_i-a_i$ （即使 $h_i-a_i=0$），在此之后第 $i$ 棵树就不会生长了。

砍树非常累，你不希望砍的树的总高度超过 $m$ 。

在满足上述条件的情况下求出 $d$ 的最大值。

Tab. $0<n\leq 100, 0\leq m\leq 10^{11}, 0< a_i\leq 10^9$

- 解析

由题意可知要求一个最大的 $d$ 满足：

$$\sum_{i=1}^n(d-a_i\bmod d)=\sum_{i=1}^n(\left\lceil\frac{a_i}{d}\right\rceil d-a_i)\leq m$$

移项可得：

$$d\sum_{i=1}^n\left\lceil\frac{a_i}{d}\right\rceil\leq m+\sum_{i=1}^na_i$$

由数论分块的知识可知 $\left\lceil\frac{a_i}{d}\right\rceil$ 最多有 $\sqrt a_i$ 种取值。对于每个 $a_i$ 枚举 $\left\lceil\frac{a_i}{d}\right\rceil$ 的取值，并求出对应的 $d$ 的取值存入 pu 数组中。将 pu 去重排序，可得 $d\in[pu_i,pu_{i+1})$ 时，$\sum_{i=1}^{n}\left\lceil\frac{a_i}{d}\right\rceil$ 的取值相同。

枚举 $d=pu_i$ ，记此时的 $\sum_{i=1}^{n}\left\lceil\frac{a_i}{d}\right\rceil$ 为 $tot$，那么 $d$ 的最大取值就为 $\frac{m}{tot}$ （如果 $pu_i\leq \frac m{tot} < pu_{i+1}$）。

- 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=100;
int n;
ll m,pu[10000004],a[N+3],npu;
int main(){
	freopen("cut.in","r",stdin);
	freopen("cut.out","w",stdout);
	scanf("%d%lld",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	for(int i=1;i<=n;i++){
		m+=a[i];
		for(int j=1;j*j<=a[i];j++)
			pu[++npu]=j,
			pu[++npu]=(ll)ceil(1.0*a[i]/j);
	}
	sort(pu+1,pu+npu+1);
	npu=unique(pu+1,pu+npu+1)-(pu+1);
	ll ans=1;
	for(int i=1;i<=npu;i++){
		ll d=pu[i],tot=0;
		for(int j=1;j<=n;j++)
			tot+=(ll)ceil(1.0*a[j]/d);
		if(m/tot>=d) ans=m/tot;
	}
	printf("%lld\n",ans);
	return 0;
}

---

· C题：超级树(tree.cpp)

- 题目

一棵 k-超级树 的构建方法如下：

1. 构造出一个 $k$ 层的满二叉树；
2. 将每个点与它的所有祖先（不包括父亲）连边；

树上的所有边都是无向边。例如下图为一棵 4-超级树：

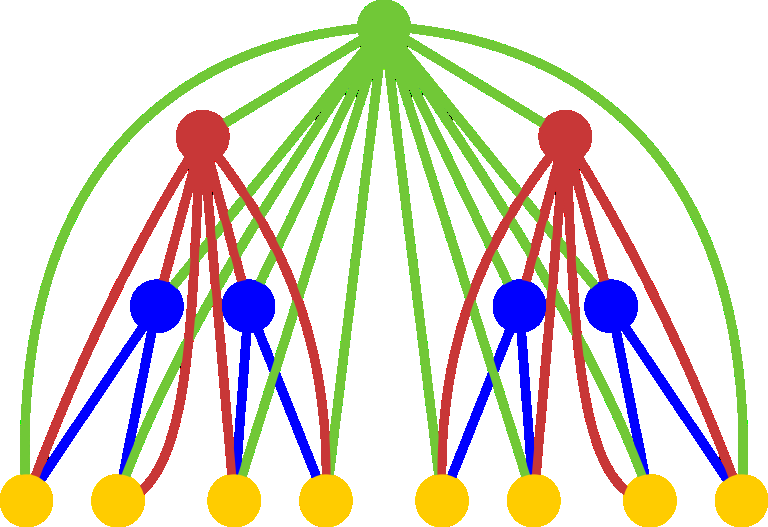
给定 $k,m$ ，求从 k-超级树 的任意一个节点出发，能够找到多少条不重复经过点的有向路径，答案取模 $m$。（不同指经过的节点不同或经过节点的顺序不同；可以不经过所有的点）

Tab. $1\leq k \leq 300, 1\leq m \leq 10^9$

- 解析

因为超级树里同一层的点的价值相同，不难想到递推（动态规划）。

令 $dp[i][j]$ 表示将 i-超级树 中划分出 $j$ 条没有相同点的路径的方案数（不一定经过所有点）。那么最后的答案就是“在 k-超级树 中划分出 $1$ 条路径的方案数”，即 $dp[k][1]$ 。

一棵 n-超级树 可以看做是左右两棵 (n-1)-超级树 的根节点 $a,b$ 连到一个新的节点 $u$ （$u$ 是 n-超级树 的根节点）上形成的。那么我们就可以得到几种转移方式（乘法原理）：
① 左右两个子树本身的路径分割方式不变，总路径数不变：dp[n][l+r]+=dp[n-1][l]*dp[n-1][r]；
② 除了左右子树本身路径，再将根节点 $u$ 划分为单独的一条路径，总路径数加一：dp[n][l+r+1]+=dp[n-1][l]*dp[n-1][r]；
③ 将左子树的某一条路径与根节点 $u$ 连边形成新的路径，总路径数不变：dp[n][l+r]+=dp[n-1][l]*l*dp[n-1][r]；
④ 将右子树的某一条路径与根节点 $u$ 连边形成新的路径，总路径数不变：dp[n][l+r]+=dp[n-1][l]*dp[n-1][r]*r；
⑤ 将左子树的某条路径经过根节点 $u$ 与右子树的某条路径相连，总路径数减一：dp[n][l+r-1]+=2*l*r*dp[n-1][l]*dp[n-1][r] ；
⑥ 将左子树的某条路径经过 $u$ 再连接到左子树的另一条路径，总路径数减一：dp[n][l+r-1]+=l*(l-1)*dp[n-1][l]*dp[n-1][r]；
⑦ 将右子树的某条路径经过 $u$ 再连接到右子树的另一条路径，总路径数减一：dp[n][l+r-1]+=r*(r-1)*dp[n-1][l]*dp[n-1][r]；

（稍微理解一下，有点难度）

- 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=300;
int n;ll mod;
ll dp[N+3][1<<11];
void Add(ll &x,ll y){x=(x+y)%mod;}
int main(){
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d%lld",&n,&mod);
	dp[1][0]=dp[1][1]=1;
	for(int i=2;i<=n;i++){
		int lim=i<=10? min((1<<i)-1,n-i+2):n-i+2;
		for(int l=0;l<=lim;l++)
			for(int r=0;l+r-1<=lim;r++){
				ll num=dp[i-1][l]*dp[i-1][r]%mod;
				Add(dp[i][l+r],num);
				Add(dp[i][l+r+1],num);
				Add(dp[i][l+r],num*2%mod*(l+r)%mod);
				Add(dp[i][l+r-1],2*num%mod*l%mod*r%mod);
				Add(dp[i][l+r-1],num*l%mod*(l-1)%mod);
				Add(dp[i][l+r-1],num*r%mod*(r-1)%mod);
			}
	}
	printf("%lld\n",dp[n][1]%mod);
	return 0;
}

---

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~