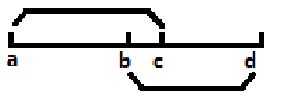之前一位同学做了这场比赛,拉到了 vjudge 组里……
就当练练手~
『A: Integer Sequence Dividing』 〔传送门〕
「题意」
将1~n的所有数分为两个集合A,B(每个数属于且尽属于一个集合),求 $|(\sum_iA_i)-(\sum_i B_i)|$ 的最小值。
「解析」
显然数学题……(我可能想复杂了)
tab.以下区间均指整数区间
先看这样一道问题:“将区间 $[i,i+4k-1],k\in \mathbb{Z}_+$ 的所有数(也就是连续 $4k$ 个正整数)分为两个集合 $A,B$,使得 $|\sum_iA_i-\sum_iB_i|$ 最小”。
可以找到一种方案:
使得 $\sum_iA_i=\sum_iB_i$,当然是最小的。
推而广之,对于区间 $[1,n]$ 可以分为 $4$ 种情况:
① $n \mod 4=0$,也就是之前提到的问题,答案为 $0$;
② $n \mod 4=1$,那么区间 $[2,n]$ 是一个长度为 $4k$ 的整数区间,这一段可以分成和相等的两个集合,那么剩下的 $1$ 分给任何一个集合都会使差增加 $1$,所以答案为 $1$;
③ $n \mod 4=2$,类比情况②,会剩下 $1,2$ ,则把它们放在不同的集合中,可以达到最小值 $1$;
④ $n \mod 4=3$,此时就会剩下 $1,2,3$,把 $1,2$ 分给一个集合,$3$ 分给另一个集合,就达到最小值 $0$;
其实不难发现——如果 $1$ 到 $n$ 的和为偶数,答案就为 $0$,否则为 $1$。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
long long n;
int main(){
scanf("%lld",&n);
printf("%lld\n",(1ll+n)*n/2ll%2ll);
return 0;
}
|
『B: Array K-Coloring』 〔传送门〕
「题意」
有 $n$ 个方块,$m$ 种颜色($m\leq n$),每个方块上有一个数字 $a_i$。你需要求出一种涂色方案,满足:
① 每个方块都有颜色;
② 每种颜色都被用过;
③ 被涂成相同颜色的方块上的数字不能相同;
如果有方案,输出”YES”并给出方案,否则输出”NO”。
「解析」
一道不错的、难度不算高的贪心题。
首先我们把第 $1$ 到 $m$ 个方块涂上 $1$ 到 $m$ 种颜色,以保证每一个颜色都出现过;然后因为每一种颜色都是等价的,我们把接下来的方块依次尝试涂上颜色,暴力检查如果该方块涂上某一种颜色,该颜色是否会存在两个方块数字相同,如果可以涂,就涂上颜色,否则就无法得到方案。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=5000;
int n,m;
vector<int> mem[N+7];
int ans[N+7];
int main(){
scanf("%d%d",&n,&m);
for(int i=1,num;i<=n;i++){
scanf("%d",&num);
if(i<=m){
ans[i]=i;
mem[i].push_back(num);
continue;
}
bool Ext=false;
for(int j=1;j<=m;j++){
bool ext=false;
for(int k=0;k<mem[j].size();k++)
if(mem[j][k]==num){
ext=true;
break;
}
if(!ext){
Ext=true;
ans[i]=j;
mem[j].push_back(num);
break;
}
}
if(!Ext) printf("NO\n"),exit(0);
}
printf("YES\n");
for(int i=1;i<=n;i++) printf("%d%c",ans[i],i==n? '\n':' ');
return 0;
}
|
『C: Doors Breaking and Repairing』 〔传送门〕
「题意」
你和另一个玩家进行一个游戏:
给出了 $n$ 个正整数和整数 $A,B$,你和对手轮流进行操作,你可以选择一个不为零的数字并将它减去 $A$(如果相减后小于$0$,则该数变为$0$),对手则选择一个不为零的数字将它加上 $B$。
当你不可能将任何数字变为 $0$ 或所有数字均为 $0$ 时,游戏结束。
假设你和对手都足够聪明,求最后你可以使多少个数字变成0。
「解析」
一道思路非常“博弈论”的题……
显然只要你能够使一个数变成0,就对它进行操作。对于 $A>B$ 的情况,显然可以全部变为 $0$。
对于 $A\leq B$ 的情况就会复杂一些,这个时候只有你能够一次将某个数变为 $0$ 时,你才可以将它变为 $0$,不然你对那个数 $-A$ ,对手又给它 $+A$,你肯定比不过对手。
考虑双方的最优策略:
① 你的策略:找到一个小于 $A$ 的数进行操作;
② 对手的策略:找到一个小于 $A$ 的数进行操作;
???什么意思???
这种情况下,如果对手对一个小于 $A$ 的数操作,它就大于 $A$ 了,此时你肯定无法使它变成 $0$。所以当你将一个小于 $A$ 的数变成 $0$ 后,对手就会把另一个小于 $A$ 的数变成大于 $A$,设原来的正整数中有 $tot$ 个小于等于 $A$,因为你是先手,你最多能够将 $\frac{tot}{2}$(向上取整) 个数变成 $0$。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,a,b,ans,tot;
int main(){
scanf("%d%d%d",&n,&a,&b);
for(int i=0,num;i<n;i++){
scanf("%d",&num);
if(b<a) ans++;
if(a<=b && num<=a)
ans++;
}
if(a<=b) ans=(ans+1)/2;
printf("%d\n",ans);
return 0;
}
|
『D: Balanced Ternary String』 〔传送门〕
「题意」
有一个长度为 $3$ 的倍数且只包含字符 0,1,2 的字符串,你需要对它的一些字符进行改动,使得 0,1,2 出现的次数相等。
求出在修改次数最少的情况下修改后字典序最小的字符串。
「解析」
又是一道贪心题……
我们先可以根据字符串长度求出每种字符各需要出现多少次,记为 $bal$。
tab.先考虑0或先考虑2是一样的
因为 0 的字典序最小,我们先考虑 0 。如果它次数小于 $bal$ ,则将尽量靠前的不为 0 且次数超过 $bal$ 的字符改为 0;
因为 2 的字典序最大,我们再考虑 2。如果它次数小于 $bal$ ,则将尽量靠后的不为 2 且次数超过 $bal$ 的字符改为 2;
如果此时 1 的个数不足 $bal$,
因为 1 字典序比 2 小,若 2 的次数大于 $bal$,我们将尽量靠前的 2 换成 1 ,直到 2 的次数为 $bal$ 为止;
因为 1 的字典序比 0 大,若 0 的次数大于 $bal$,我们将尽量靠后的 0 换成 1,直到 0 的次数为 $bal$ 为止;
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=(int)3e5;
int n,bal;
char str[N+7];
int cnt[3];
int main(){
scanf("%d%s",&n,str+1);
for(int i=1;i<=n;i++)
cnt[str[i]-'0']++;
bal=n/3;
for(int i=1;i<=n && cnt[0]<bal;i++)
if(cnt[str[i]-'0']>bal)
cnt[str[i]-'0']--,
str[i]='0',
cnt[str[i]-'0']++;
for(int i=n;i>=1 && cnt[2]<bal;i--)
if(cnt[str[i]-'0']>bal)
cnt[str[i]-'0']--,
str[i]='2',
cnt[str[i]-'0']++;
for(int i=1;i<=n && cnt[1]<bal && cnt[2]>bal;i++)
if(str[i]=='2')
cnt[str[i]-'0']--,
str[i]='1',
cnt[str[i]-'0']++;
for(int i=n;i>=1 && cnt[1]<bal && cnt[0]>bal;i--)
if(str[i]=='0')
cnt[str[i]-'0']--,
str[i]='1',
cnt[str[i]-'0']++;
printf("%s\n",str+1);
return 0;
}
|
『E: Monotonic Renumeration』 〔传送门〕
「题意」
给出一个长度为 $n$ 的序列 $A$,根据 $A$ 构造长度为 $n$ 的序列 $B$,满足:
① 若 $A_i=A_j$,则 $B_i=B_j$;
② $B_i-B_{i-1}\leq 1$
求能够构造出的 $B$ 的个数。
「解析」
非常巧妙~还好 C++ 有STL容器。
如果 $A_i=A_j(i < j)$,不难推出 $B_i$ 到 $B_j$ 的所有数应该相同。那么我们就可以得到:
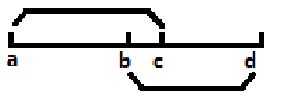
上图中 $A_a=A_c,A_b=A_d$,则 $B_k(k\in[a,d])$ 全部相同。就相当于我们把 $A_i=A_j$ 的 $i,j(i\leq j)$ 看成区间 $[i,j]$,如果两个区间相交,则取两个区间的并集,这个集合里的所有 $B_k$ 都相等。
这样的话 $B$ 就被分成了一些区间,相邻区间的元素的值要么相等,要么右边区间值比左边大 $1$,这样的话方案就是一个组合数,假设 $B$ 被分成的区间有 $tot$ 个,则方案数为 $2^{tot-1}$ ,快速幂就好了。
至于求区间,就交给 STL map了。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
const int N=(int)2e5;
const long long MOD=998244353ll;
int n;
int num[N+7];
map<int,pair<int,int> > mem;
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&num[i]);
for(int i=0;i<n;i++)
mem[num[i]].first=min(mem[num[i]].first,i),
mem[num[i]].second=max(mem[num[i]].second,i);
int to=0;
long long ans=1;
for(int i=0;i<n;i++){
if(i<=to)
to=max(to,mem[num[i]].second);
else
ans=ans*2%MOD,
to=mem[num[i]].second;
}
printf("%lld\n",ans);
return 0;
}
|
『F: Elongated Matrix』 〔传送门〕
「题意」
给出一个 $r\times c$ 的矩阵,将它的第$i$列的尾部接上第$i+1$列的开头,构成一个序列,令这个序列的相邻元素的差的绝对值的最小值为 $S$。
你可以交换矩阵的行,使得 $S$ 最大,求最大的 $S$。
「解析」
看数据规模容易想到状压。
定义 dp[T][i] 表示已经确定的行为 $T$(状压的状态),且当前最后一行为第$i$行的最大 $S$。
预处理一个 val[i][j] 表示将第$i$行接在第$j$行后面时,它们之间的数值之差的最小值。
那么我们可以得到状态转移方程式:
不难理解就是把第$i$行放在第$j$行后面。
好像缺了什么?首尾相接?第一行放哪一行也会产生影响。
由于规模不大,可以直接枚举第一行,再进行dp转移,假设确定第一行为 $fir$。我们再初始化一个 $val1[i][j]$ 表示 第一行放第$i$行、最后一行放第$j$行首尾相接后的相邻元素的差的最小值。
那么最后的答案就是 $\min(dp[\{x|1\leq x\leq n\}][i],val1[fir][i])$。
由于加了这么一个条件,我们需要在转移时判断第一行是否重复(即枚举时除非当前时第2行,上一行就不能是已经确定的第一行)。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int R=16,C=(int)1e4;
int r,c,INF,ans;
int mat[R+7][C+7],val[R+7][R+7][2],dp[(1<<R)+7][R+7];
bool vis[(1<<R)+7];
queue<int> que;
inline int Qabs(int num){return num>=0? num:-num;}
#define belong(a,b) (a&(1<<b))
int main(){
memset(val,0x3f,sizeof val);
INF=val[0][0][0];
scanf("%d%d",&r,&c);
for(int i=0;i<r;i++)
for(int j=0;j<c;j++)
scanf("%d",&mat[i][j]);
if(r==1){
ans=INF;
for(int i=1;i<c;i++)
ans=min(ans,Qabs(mat[0][i]-mat[0][i-1]));
printf("%d\n",ans);
return 0;
}
for(int i=0;i<r;i++)
for(int j=0;j<r;j++)
if(i!=j){
for(int k=0;k<c;k++)
val[i][j][0]=min(val[i][j][0],Qabs(mat[i][k]-mat[j][k]));
for(int k=0;k<c-1;k++)
val[i][j][1]=min(val[i][j][1],Qabs(mat[j][k]-mat[i][k+1]));
}
for(int fir=0;fir<r;fir++){
memset(vis,false,sizeof vis);
memset(dp,-1,sizeof dp);
que.push(1<<fir);
dp[1<<fir][fir]=INF;
int cnt=0;
while(!que.empty() && ++cnt){
int pre=que.front();que.pop();
for(int nxt=0;nxt<r;nxt++)
if(!belong(pre,nxt)){
int id=pre|(1<<nxt);
for(int lst=0;lst<r;lst++)
if(belong(pre,lst)){
if(lst==fir && cnt>r) continue;
dp[id][nxt]=max(dp[id][nxt],min(val[lst][nxt][0],dp[pre][lst]));
if(id!=(1<<r)-1 && !vis[id]) vis[id]=true,que.push(id);
}
}
}
for(int lst=0;lst<r;lst++)
ans=max(ans,min(dp[(1<<r)-1][lst],val[fir][lst][1]));
}
printf("%d\n",ans);
return 0;
}
|
The End
Thanks for reading!
Email: lucky_glass@foxmail.com ,欢迎提问~