这是老师选出来的3道题,感觉质量还不错……可以做一下~
包含 Codeforces Educational Round 57 的 C、D、F题
『C: Polygon for the Angle』〔传送门〕
「题意」
给出一个角度 $ang(ang < 180)$(角度制),求最小的整数 $n(n > 2)$ 表示正n边形中,选择其中3个
不同的顶点,可以构造出一个角度为 $ang$ 的角。
$T$ 组询问,每组询问给出一个 $ang$,输出对应的 $n$。($T\leq 180$)
「解析」
显然对于一个正多边形,它的所有顶点都共圆。
我们可以把“选择3个顶点构成一个角”改成这样:
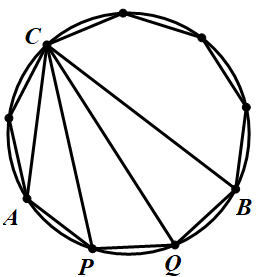
则有 $\angle ACB=\angle ACP+\angle PCQ+\angle QCB$。由于 $AP=PQ=QB$,根据“等弦対等角”,我们可以得到 $\angle ACP=\angle PCQ=\angle QCB$。
我们不妨设 $A,B$ 为多边形的一条边的两端点,$C$ 为除此之外的另外一个顶点。我们称 $\angle ACB$ 为该多边形的“单位角”。这就意味着任意选择这个多边形的3个不同的顶点,得到的角必定可以由单位角构成——也就是如果角度为 $ang$ 的角能够在正n边形中构造出来,则 $ang$ 一定是单位角的倍数!
根据上面的结论,只要我们计算出正n边形的单位角,我们就可以判断能否构造出 $ang$。
如何求单位角?其实很好理解。比如上面给出的正9边形,它的一个顶角是 $140^\circ$,如果把某一个顶角的顶点与其他所有点连边,就可以把它等分为 $(9-2)$ 份,每一份就是一个单位角,那么正9边形的单位角就是 $140^\circ / (9-2)=20^\circ$。给出结论:正n边形的单位角为 $\frac{180^\circ - 360^\circ/n}{n-2}$。
因为正360边形的单位角是 $0.5^\circ$,所以答案最大为360,直接枚举判断是否可能就可以了。
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const double EPS=1e-7;
int main(){
int T;scanf("%d",&T);
while(T--){
int ang;scanf("%d",&ang);
for(int i=3;i<=360;i++){
double perang=(180.0-360.0/i)/(i-2.0);
if(ang>180.0-360.0/i) continue;
double cnt=ang/perang;
if(cnt==(int)cnt){
printf("%d\n",i);
break;
}
}
}
return 0;
}
|
『D: Easy Problem』〔传送门〕
「题意」
给出一个长度为 $n$ 的字符串,你可以删除一些字符,使得字符串中没有子序列是”hard”。删除原串中的第i个字符的花费是 $cst[i]$ ,求最小花费。
「解析」
把 ‘h’,’a’,’r’,’d’ 依次编号为 1~4。$dp[i][j]$ 表示处理到第$i$位后,子序列匹配状态为$j$ (j为1时表示存在子序列”h”,为2时表示存在子序列”ha”,为3时表示存在子序列”har”,为4时表示存在子序列”hard”)的最小花费。依次枚举 $i$ 从 $1$ 到 $n$ :
- 如果第 $i$ 位不是 “hard” 的一个字符,则不会产生影响,$dp[i][k]=dp[i-1]k$。
- 如果第 $i$ 位字符的编号是$ID$,
如果让当前子序列匹配到状态 $ID$,则 $dp[i][ID]=dp[i][ID-1]$;
如果删除当前位避免匹配,则 $dp[i][ID-1]=dp[i-1][ID-1]+cst[i]$;
其他的不会产生影响,$dp[i][j]=dp[i-1][j] (j\neq ID 且 j\neq ID-1)$。
其实这里dp的第一维可以删掉,因为它只涉及 i 和 i-1 的转移~
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5;
const ll INF=(1ll<<59);
int n;
ll cst[N+7],dp[5];
char str[N+7];
inline int GetID(char c){
switch(c){
case 'h': return 1;
case 'a': return 2;
case 'r': return 3;
case 'd': return 4;
default: return -1;
}
}
int main(){
scanf("%d",&n);
scanf("%s",str+1);
for(int i=1;i<=n;i++) scanf("%lld",&cst[i]);
dp[0]=0;dp[1]=dp[2]=dp[3]=dp[4]=INF;
for(int i=1;i<=n;i++){
int ID=GetID(str[i]);
if(ID==-1) continue;
dp[ID]=min(dp[ID],dp[ID-1]);
dp[ID-1]+=cst[i];
}
printf("%lld\n",min(min(dp[0],dp[1]),min(dp[2],dp[3])));
return 0;
}
|
『F: Inversion Expectation』〔传送门〕
「题意」
有一个 $1$ 到 $n$ 的排列,但是里面有一些元素是不确定的(用 $-1$ 表示)。
对于每一种可能出现的排列的情况(假设每种情况的概率是相同的),求出排列中逆序对的期望数量。
「解析」
肯定不可能去计算情况……所以我们把问题转化成求贡献!
把逆序对的计算分成3种情况:
- 两个确定的数:这是完全确定的——对于每一个数,它的贡献就是左边比它大的数的个数,可以用树状数组来维护左边的数。
- 两个不确定的数:要么左边的数比右边的数大,要么右边的数比左边的数大,这样两种情况的概率是相等的,所以对于一个未确定的数,它有 $\frac{1}{2}$ 的概率能够和另外一个未确定的数构成逆序对,也就是说每一个可能出现的逆序对的概率都是 $\frac{1}{2}$,所以总贡献就是 $\frac{cnt*(cnt-1)}{4}$($cnt$是未确定数的数量)。
- 一个确定的数和一个不确定的数:我们从确定的数开始考虑,则左边的未确定的数比它大或右边的未确定的数比它小就可以构成逆序对。我们定义 $grt[i]$ 表示比 $i$ 大的未确定数的数量。那么令那个确定的数为 $A$,它左边未知的数的个数为 $lef$,右边未知的数的个数为 $rig$,它的期望贡献就是 $\frac{lef * grt[A] + rig * (cnt-grt[A])}{cnt}$
最后3种情况的期望加起来就是答案~
「源代码」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define lowbit(x) (x&-x)
typedef long long ll;
const int N=(int)2e5;
const ll MOD=998244353ll;
int n,ukcnt;
ll ans,ukcnt_inv;
int num[N+7],grt[N+7],tre[N+7];
bool knw[N+7];
inline ll QMul(ll a,ll b){return (a%MOD)*(b%MOD)%MOD;}
inline ll QAdd(ll a,ll b){return (a+b)%MOD;}
ll QPow(ll a,ll b){
ll ret=1;
while(b){
if(b&1) ret=QMul(ret,a);
a=QMul(a,a);
b>>=1;
}
return ret;
}
void Update(int x){
while(x<=n){
tre[x]++;
x+=lowbit(x);
}
}
int Query(int x){
int ret=0;
while(x){
ret+=tre[x];
x-=lowbit(x);
}
return ret;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&num[i]);
if(num[i]!=-1) knw[num[i]]=true;
}
for(int i=n;i>=1;i--){
grt[i]=ukcnt;
ukcnt+= (!knw[i]);
}
ans=QMul(QMul(ukcnt,ukcnt-1),QPow(4ll,MOD-2));
ukcnt_inv=QPow(ukcnt,MOD-2);
int lef=0;
for(int i=1;i<=n;i++)
if(num[i]==-1)
lef++;
else
ans=QAdd(ans,QMul(lef,QMul(grt[num[i]],ukcnt_inv)));
int rig=0;
for(int i=n;i>=1;i--)
if(num[i]==-1)
rig++;
else
ans=QAdd(ans,QMul(rig,QMul(ukcnt-grt[num[i]],ukcnt_inv)));
for(int i=1,cnt=0;i<=n;i++)
if(num[i]!=-1){
ans=QAdd(ans,cnt-Query(num[i]));
Update(num[i]);
cnt++;
}
printf("%d\n",ans);
return 0;
}
|
The End
Thanks for reading!
Email: lucky_glass@foxmail.com ,欢迎提问~
