OI题解 - CF Round #524 Div.2 | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI题解 - CF Round #524 Div.2

发表于 更新于 分类于 Valine：

不容易CF有一场下午的比赛，开心的和一个神犇一起报了名
被虐爆……前两题水过去，第三题卡了好久，第四题毫无头绪QwQ
Codeforces 传送门
Tab, 先写了ABC题，后面的之后再补 QwQ

『解析』

A-Petya and Origami

读懂题意就会做……根据题意可以求出3种”sheet”各自需要的数量，然后每一种的数量除以k向上取整后求和就是答案。

B-Margarite and the best present

简单的数学题，根据题意可以将数列分成两部分：

hh……两个等差数列。稍微注意一下左右两端点的值然后等差数列求和就可以了

C-Masha and two friends

没看懂官方给的那个算法标签是什么……
在这里插入图片描述
(@_@) 不管，反正我觉得我的算法没问题……（其实主要想讲这道题）
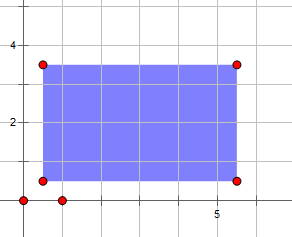
首先进行的操作是将闭区间变成左开右闭区间和上开下闭区间，这样的效果就是这样：

原来的左下角为$(0,0)$，右上角为$(5,3)$的矩形是这样：
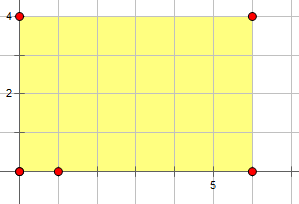
在这里插入图片描述
进行操作过后就长这样：
在这里插入图片描述
可以看出来两种矩形覆盖到的方格的个数是一样的……

这步操作主要是为了方便判断重叠。
然后把矩形存成了一个存储了上下左右边界（u,d,l,r）的结构体，然后根据它的左下角坐标和长宽就可以算出它里面的黑白格子分别有多少个。
for example……

比如左下角为$(0,0)$，右上角为$(4,4)$的矩形，
因为左下角的格子是白色的，所以这个矩形里白色一定不比黑色少（比较简单）
又因为它的长宽是3,3（这里看格子的个数），所以面积为9，较多的格子有5个，另一种格子有4个。
所以白色有5个，黑色有4个。

接下来就套用漂浮法：先在第一层放上黑色的矩形（下面称矩形A）（因为题目中它是最后一个放上去的矩形），然后尝试漂浮白色的矩形（下面称矩形B）——如果与矩形A没有重叠，则全部漂浮上去；否则如果矩形B的左边与矩形A重叠，就把矩形B按矩形A的左边界分为左右两半，etc.
再举个例子：

如果矩形B的右边与矩形A相交，那么分割就会像这样：
在这里插入图片描述

OK~切下来的矩形都会“漂浮”上去，对这些矩形统计涂色后各颜色块的变化数量就可以了~

D-Olya and magical square

另外写了一篇博客$QwQ$

『源代码』

A-Petya and Origami

1
2
3
4
5
6
7
8
9
10
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,k;
	scanf("%d%d",&n,&k);
	double A=n*2,B=n*5,C=n*8;
	printf("%lld\n",(long long)ceil(A/k)+(long long)ceil(B/k)+(long long)ceil(C/k));
	return 0;
}

B-Margarite and the best present

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
int main(){
	int T;scanf("%d",&T);
	while(T--){
		long long l,r;
		scanf("%lld%lld",&l,&r);
		long long fl,fr,gl,gr;
		if(l%2) fl=l,gl=l+1;
		else gl=l,fl=l+1;
		if(r%2) fr=r,gr=r-1;
		else gr=r,fr=r-1;
		long long ans=0;
		if(gl<=gr) ans+=(gl+gr)*((gr-gl)/2+1)/2;
		if(fl<=fr) ans-=(fl+fr)*((fr-fl)/2+1)/2;
		printf("%lld\n",ans);
	}
	return 0;
}

C-Masha and two friends

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5;
struct SQUARE {
	int l,r,u,d,col;
	pair<ll,ll> GetArea() {
		ll R=u-d,C=r-l,A,B;
		if(C%2) {
			if(R%2) A=R/2*C+C/2+1,B=R/2*C+C/2;
			else A=R/2*C,B=R/2*C;
		} else {
			if(R%2) A=R/2*C+C/2,B=R/2*C+C/2;
			else A=R/2*C,B=R/2*C;
		}
		if(d%2==l%2) return make_pair(A,B);
		else return make_pair(B,A);
	}
} squ[N+5];
int n;
ll wht,blk;
void Floatage(int dep,SQUARE now) {
	if(now.l>=now.r || now.d>=now.u) return;
	while(dep<=n && (now.l>=squ[dep].r || now.r<=squ[dep].l || now.u<=squ[dep].d || now.d>=squ[dep].u))
		dep++;
	if(dep>n) {
		pair<ll,ll> _now=now.GetArea();
		if(now.col) wht-=_now.first,blk+=_now.first;
		else wht+=_now.second,blk-=_now.second;
		return;
	}
	SQUARE las=squ[dep],nxt;
	if(now.l<las.l) {
		nxt=now;
		nxt.r=las.l;
		Floatage(dep+1,nxt);
		now.l=las.l;
	}
	if(now.r>las.r) {
		nxt=now;
		nxt.l=las.r;
		Floatage(dep+1,nxt);
		now.r=las.r;
	}
	if(now.u>las.u) {
		nxt=now;
		nxt.d=las.u;
		Floatage(dep+1,nxt);
		now.u=las.u;
	}
	if(now.d<las.d) {
		nxt=now;
		nxt.u=las.d;
		Floatage(dep+1,nxt);
		now.d=las.d;
	}
}
int main() {
	int T;
	scanf("%d",&T);
	while(T--) {
		SQUARE bak;
		bak.l=bak.d=1;
		n=2;
		scanf("%d%d",&bak.u,&bak.r);
		bak.u++;bak.r++;
		pair<ll,ll> _bak=bak.GetArea();
		wht=_bak.first,blk=_bak.second;
		for(int i=0; i<2; i++) //left,down,right,up
			scanf("%d%d%d%d",&squ[i].l,&squ[i].d,&squ[i].r,&squ[i].u),squ[i].col=i,
			squ[i].r++,squ[i].u++;
		for(int i=1; i>=0; i--)
			Floatage(i+1,squ[i]);
		printf("%lld %lld\n",wht,blk);
	}
	return 0;
}

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~