寒假学习开始……
『算法简述』
一种非常神奇的数据结构,基于二叉排序树(但是也可以完全不一样,只是一棵二叉树),虽然并非完全意义上的“平衡树”,我们一般还是把它当做平衡树用~
具有优点:
① 好想+好写+log级别(相较于平衡树);
② 能实现平衡树不能实现的区间操作;
③ 能实现线段树不能实现的加点删点;
④ 有的时候我们不一定要让它满足“堆”的性质;
主体为非常神奇的Splay伸展操作!(Tab. 这也是为什么它被叫做Splay、(自底向上)伸展树,但是它的原作者给出的命名为“自适应伸展树”,也就是说它不需要像其他平衡树一样刻意维护平衡,会“自适应”)
『理论依据简述』
根据势函数分析,对于一棵Splay,真正被访问很多次的点大约只有 $10\%$ ,这就意味着如果我们把这 $10\%$ 提到比较靠近根节点的位置,我们访问的速度会加快很多。这就是为什么基本上每进行一次操作,都要将被操作的点通过一些操作(下面讲的 Splay操作)提升到根节点。
『结构』
1 | struct NODE{ |
一般来说就是上面这种结构。像线段树一样,我们还可以往里面塞各种各样我们要用的变量。指针变量ch是它的左右儿子(ch[0] 是左儿子),fa是它的父亲。siz 是当前点的子树的大小;key 是一般情况下二叉排序树点的键值,对于每个点满足左儿子的key小于该点的key小于右儿子的key。
* :什么是一般情况呢?在下面我们会讲到Splay支持的“查询某个值在Splay中的排名”等操作,必须要求Splay有二叉排序树的性质。但是并不是总要满足,比如在“文艺平衡树”一题中,要求区间翻转,这个时候Splay扮演了线段树的角色,需要交换左右儿子,就会破坏二叉排序树性质。后面会再提到。
另外我们会有几个特殊指针变量:ncnt,NIL和root —— ncnt 指向当前的一个新节点,在创建新节点时使用;NIL 是一个空指针,代替NULL,防止NULL指针访问出错;root 指向当前的空节点。
那么我们需要初始化 Splay(重建Splay):
1 | inline void Rebuild(){ |
『Rotate旋转 & Splay伸展』
这是Splay里面最为重要的两个函数。
类似于大多数平衡树,Splay的调整平衡是通过旋转操作完成的,旋转操作是基于原本的二叉排序树性质完成的,也就是说如果最初的Splay满足二叉排序树性质,Rotate过后同样满足。
「单旋」
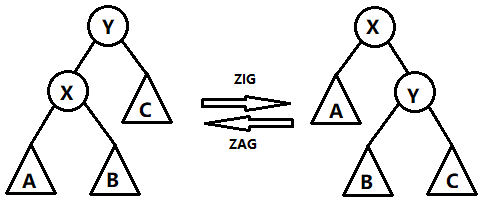
如上图所示,我们要让X移动到Y的位置去,但是不能破坏二叉排序树的性质($A<X<B<Y<C$),那么我们使用到了Rotate操作,分为左旋ZAG、右旋ZIG。为了简化代码,我们这里定义方向变量 $dir$ —— $dir=0$ 表示右旋,$dir=1$ 表示左旋。
根据上图的形式,以右旋为例。我们可以看到 X 的右儿子 B 变为了 Y 的左儿子,X Y 互换了位置。那么我们可以把右旋拆解为 $4$ 步:
① 将 Y 的左儿子的指针改为 X 的右儿子,(如果X有右儿子)X的右儿子的父亲指针指向 Y;
② 将 X 的父亲指针指向 Y 的父亲,(如果 Y 有父亲)Y 的父亲的原来指向 Y 的指针指向 X;
③ X 的右儿子指向 Y , Y 的父亲指向 X;
④ 如果 Y 原来是 root,root 指向 X;
最后统计 Y 的子树的大小,这里打包成PushUp函数,很好理解,就不单独写了,见最后源代码。(至于为什么不统计 X 的子树大小我还没弄清楚,希望有高见的 reader 能够在 email 中回复我)
另外左旋是刚好相反的,可以通过 $dir$ 实现~1
2
3
4
5
6
7
8
9inline void Rotate(NODE *x){
NODE *y=x->fa;
int dir=(y->ch[0]==x); //0 ZIG;1 ZAG 直接在内部计算是左旋还是右旋
x->fa=y->fa;if(y->fa!=NIL) y->fa->ch[y->fa->ch[1]==y]=x;
y->ch[!dir]=x->ch[dir];if(x->ch[dir]!=NIL) x->ch[dir]->fa=y;
x->ch[dir]=y;y->fa=x;
if(root==y) root=x;
PushUp(y);
}
「双旋」
直线式: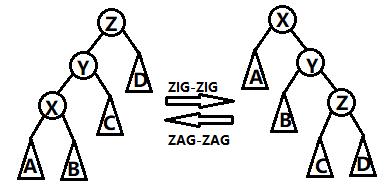
注意顺序!虽然是两次单旋,但是先旋转 Y,再旋转 X !(不然旋转出来不一样……反向操作还无法还原)
折线式: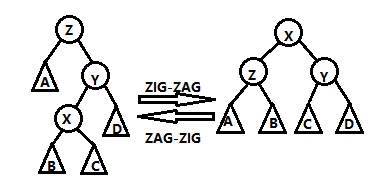
这次是两次旋转 X!
建议reader们都试一试~
「Splay伸展」
它的操作内容是:把一个点x通过一系列旋转将它旋转到它的某一个祖先rt的下方(尽可能用双旋)。
设 x 的父亲为 y,祖父为 z;
① z 就是 rt:此时我们只需要最后单旋一次,所以 Rotate(x) 即可;
② 否则就用双旋 —— 判断 x,y,z 三点是“直线式”还是“折线式”,方法见代码,然后决定旋转的先后;
③ 直到旋转到 rt 下方为止(也就是x是rt的一个儿子);
1 | void Splay(NODE *x,NODE *rt){ |
『NewNode新建节点 & Insert插入』
这里我们用了NewNode()来新建一个节点——找到新节点指针ncnt,保存为指针 p,p的儿子、父亲指针初始值全赋值为 NIL,键值key作为参数_key传入NewNode()。最后返回这个指针。
1 | inline NODE *NewNode(int _key){ |
Insert插入操作是基于二叉排序树性质的,虽然即使不满足也可以完成。大概就是从根节点开始,判断插入的值_key 与当前点键值的大小关系从而确定它属于当前点的左子树还是右子树(默认一个规则:如果_key与当前键值相同,我们定义要插入的这个值“小于”当前点,属于左子树;除非在一些题中把相同的值压入同一个点,对每个点记录cnt表示这个值总共有多少个)。直到访问到一个空节点,则在该节点创建新节点,修改它的父亲节点,最后Splay到根节点。
1 | void Insert(NODE *&rt,NODE *pre,int _key){ //rt的取值符 '&' 不能少! |
『Find查找值 & FindPre前驱 & FindNxt后继 & FindMaxMin极值』
「Find查找特定值」【基于二叉排序树的性质】
Tab. 如果存在多个相同的值,我们找的是最后插入 $Splay$ 的一个节点
从根节点开始查找;如果当前点的键值小于查找值,那就继续找右儿子,否则找左儿子(因为在Insert的时候如果插入值和当前值相等,我们把新值传给了左儿子,所以现在找的时候如果相等是找左儿子)。
如果找到给定值了,我们就把找到的点 Splay 到根,然后返回这个点;
但是如果没有呢,也就是说我们找到了一个NIL节点?我们不会白找一遍,还是会返回该NIL节点的父亲,并把这个父亲节点 Splay 到根。1
2
3
4
5
6
7
8
9
10
11
12
13
14NODE *Find(NODE *rt,int key){
if(rt==NIL) return NIL;
NODE *p;
if(key==rt->key){
p=rt->ch[0];
while(p->ch[0]!=NIL && p->key==key) rt=p,p=p->ch[0];
Splay(rt,NIL);
return rt;
}
if(key<rt->key) p=Find(rt->ch[0],key);
else p=Find(rt->ch[1],key);
if(p==NIL) p=rt,Splay(rt,NIL);
return p;
}
「FindPre查找前驱 & FindNxt查找后继」【基于二叉排序树的性质】
以查找 $X$ 的前驱为例;
大概过程是从根节点出发,如果当前点的键值小于 $X$,就找当前位置的右儿子,否则找到左儿子,一直找到一个空节点 NIL,然后返回 NIL 开始回溯。
回溯过程中找到第一个小于 $X$ 点,这就是 $X$ 的前驱。
然后 $X$ 的后继是反过来的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20inline NODE *FindPre(NODE *rt,int key){
NODE *p;
if(rt==NIL) return NIL;
if(key>rt->key){
p=FindPre(rt->ch[1],key);
if(p==NIL) p=rt,Splay(p,NIL);
}
else p=FindPre(rt->ch[0],key);
return p;
}
inline NODE *FindNxt(NODE *rt,int key){
NODE *p;
if(rt==NIL) return NIL;
if(key<rt->key){
p=FindNxt(rt->ch[0],key);
if(p==NIL) p=rt,Splay(p,NIL);
}
else p=FindNxt(rt->ch[1],key);
return p;
}
「FindMinMax 查找极值」【基于二叉排序树的性质】
非常简单的思路,因为满足二叉排序树性质,找最大值就是一直找右儿子,最小值就是一直找左儿子。1
2
3
4
5
6
7NODE *FindMinMax(NODE *rt,bool Min_Max){
idf(rt==NIL) return NIL;
NODE *p=rt;
while(p->ch[Min_Max]!=NIL) p=p->ch[Min_Max];
Splay(p,NIL);
return p;
}
『Select查找排名第k个 & GetRank查找给定值排名』
这里排名$k$的定义是键值第 $k$ 小的点,如果两个点键值相等,我们规定先插入的点排名更高。
「Select查找排名第k的点」【基于二叉排序树的性质】
假设我们要求排名为 $rnk$ 的点(保证存在),我们把问题引申为 “以 $rt$ 为根的子树中的排名为 $rnk$ 的点”。
那么我们一开始的 $rt$ 就是根节点 $root$。
因为满足二叉排序树性质,$rt$ 的左子树的所有点的排名都比 $rt$ 小,右子树都比 $rt$ 大。所以 $rt$ 在以 $rt$ 为根的子树中的排名就是 “左子树大小 + $1$”。如果 $rnk$ 就等于 “左子树大小 + $1$”,就说明 $rt$ 就是我们要找的点;如果小于 “左子树大小 + $1$”,就说明我们要找的点在左子树,且该点在左子树中的排名仍然是 $rnk$;如果大于 “左子树大小 + $1$”,就说明我们要找的点在右子树,且该点在右子树中的排名为 “$rnk$ - 左子树大小 - $1$”。
递推查找即可,最后把找到的点 Splay 到根。1
2
3
4
5
6
7
8
9
10NODE *Select(int rnk,NODE *rt){
NODE *p=root;
while(true){
if(rnk==p->ch[0]->siz+1) break;
if(rnk<p->ch[0]->siz+1) p=p->ch[0];
else rnk-=p->ch[0]->siz+1,p=p->ch[1];
}
Splay(p,rt);
return p;
}
「GetRank查找给定值排名」【基于二叉排序树的性质】
从根节点出发,不一定给定值是 Splay 里的点。
由于二叉排序树性质:如果给定值小于当前点的键值,那么给定值的排名就是 “给定值在左子树内的排名”;否则给定值的排名比左子树所有点和当前点都大,则排名为 “给定值在右子树中的排名 + 左子树大小 + $1$” ;递归计算,如果当前点为 NIL,则返回 $1$。
1 | int GetRank(NODE *rt,int key){ |
『Delete删除给定值节点』【基于二叉排序树的性质】
非常巧妙,我们先找到给定值的排名 $rnk$。然后先将排名为 $rnk-1$ 的点 Splay 到根,再把排名为 $rnk+1$ 的点 Splay 到当前根节点的下方。那么我们会发现:
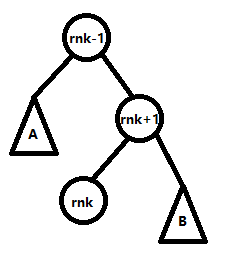
我们要删除的点被移动到排名为 $rnk+1$ 的点的左儿子去了,那么此时这个点没有子节点,我们要删除它只需要将 $rnk+1$ 的点的左儿子删除(改为 NIL)就可以了。
1 | void Delete(NODE *rt,int key){ |
『源代码』
打了包,直接可以用的~1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114struct SPLAY{
struct NODE{
NODE *ch[2],*fa;
int key,siz;
}tre[N+7];
NODE *root,*ncnt,*NIL;
inline void Rebuild(){
NIL=ncnt=&tre[0];
NIL->key=-INF;
root=NIL->ch[0]=NIL->ch[1]=NIL->fa=NIL;
}
inline NODE *NewNode(int _key){
NODE *p=++ncnt;
p->fa=p->ch[0]=p->ch[1]=NIL;
p->key=_key;p->siz=1;
return p;
}
inline void PushUp(NODE *x){x->siz=x->ch[0]->siz+x->ch[1]->siz+1;}
inline void Rotate(NODE *x){
NODE *y=x->fa;
int dir=(y->ch[0]==x); //1 ZIG;2 ZAG
x->fa=y->fa;if(y->fa!=NIL) y->fa->ch[y->fa->ch[1]==y]=x;
y->ch[!dir]=x->ch[dir];if(x->ch[dir]!=NIL) x->ch[dir]->fa=y;
x->ch[dir]=y;y->fa=x;
if(root==y) root=x;
PushUp(y);
}
void Splay(NODE *x,NODE *rt){
NODE *y,*z;
while(x->fa!=rt){
y=x->fa;z=y->fa;
if(z==rt) Rotate(x);
else{
if((z->ch[0]==y)^(y->ch[0]==x)) Rotate(x);
else Rotate(y);
Rotate(x);
}
}
}
void Insert(NODE *&rt,NODE *pre,int _key){
if(rt==NIL){
rt=NewNode(_key);rt->fa=pre;
Splay(rt,NIL);
return;
}
rt->siz++;
int dir=(_key>rt->key);
Insert(rt->ch[dir],rt,_key);
}
NODE *Find(NODE *rt,int key){
if(rt==NIL) return NIL;
NODE *p;
if(key==rt->key){
p=rt->ch[0];
while(p->ch[0]!=NIL && p->key==key) rt=p,p=p->ch[0];
Splay(rt,NIL);
return rt;
}
if(key<rt->key) p=Find(rt->ch[0],key);
else p=Find(rt->ch[1],key);
if(p==NIL) p=rt,Splay(rt,NIL);
return p;
}
inline NODE *FindPre(NODE *rt,int key){
NODE *p;
if(rt==NIL) return NIL;
if(key>rt->key){
p=FindPre(rt->ch[1],key);
if(p==NIL) p=rt,Splay(p,NIL);
}
else p=FindPre(rt->ch[0],key);
return p;
}
inline NODE *FindNxt(NODE *rt,int key){
NODE *p;
if(rt==NIL) return NIL;
if(key<rt->key){
p=FindNxt(rt->ch[0],key);
if(p==NIL) p=rt,Splay(p,NIL);
}
else p=FindNxt(rt->ch[1],key);
return p;
}
NODE *FindMinMax(NODE *rt,bool Min_Max){
if(rt==NIL) return NIL;
NODE *p=rt;
while(p->ch[Min_Max]!=NIL) p=p->ch[Min_Max];
Splay(p,NIL);
return p;
}
int GetRank(NODE *rt,int key){
if(rt==NIL) return 1;
if(key>rt->key) return rt->ch[0]->siz+1+GetRank(rt->ch[1],key);
else return GetRank(rt->ch[0],key);
}
NODE *Select(int rnk,NODE *rt){
NODE *p=root;
while(true){
// PushDown(p);
if(rnk==p->ch[0]->siz+1) break;
if(rnk<p->ch[0]->siz+1) p=p->ch[0];
else rnk-=p->ch[0]->siz+1,p=p->ch[1];
}
Splay(p,rt);
return p;
}
void Delete(NODE *rt,int key){
int rnk=GetRank(rt,key);
NODE *p=Select(rnk-1,NIL);
NODE *q=Select(rnk+1,p);
q->ch[0]=NIL;
Splay(q,NIL);
}
};
The End
Thanks for reading!
Email: lucky_glass@foxmail.com ,欢迎提问~