#Lucky_Glass挖坑不填的日常#（我明天就填咕）
# 引入
想必大家都知道高斯消元，虽然它写法多样，但实际上思想都是一样的，就不多加阐述了。
众所周知高斯消元是 $O(n^3)$ 的（$n$ 是未知数的数量，一般来说也是等式的数量）。有一些题目，虽然 $n$ 很大，但是与 $x_i$ 有关的变量（出现在 $x_i$ 的等式中的变量）的范围为 $x_{i-d}\text~x_{i+d}$，其中 $d$ 比较小，这样的话可以把复杂度优化到 $O(nd^2)$。
如果你把满足上述条件的所有等式画成一个矩阵，你会发现 所有非零元素（除了最后一列常数项）位于距离对角线 ±d 的范围内。对这样的矩阵进行高斯消元，称作带状矩阵的高斯消元。
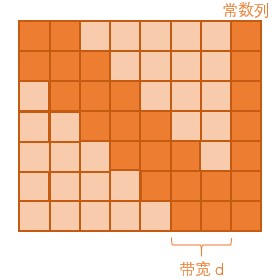
(图 带状矩阵的一个栗子)
# 巧妙地“偷懒”
用第 $i$ 行对 $i+1$ 行到 $\min\{i+d,n\}$ 进行消元，使得这些行的 $x_i$ 的系数变为 $0$。
注意只是往下 $d$ 行，并不消 $(i,i)$ 上方的值。
而且我们发现：我们发现消到第 $i$ 行时，第 $i$ 行最多只有 $d$ 个非零元素（因为对角线左边的也被消完了）；所以只要枚举 $d$ 个未知数进行消元。
因为非零元素与对角线的距离都在 $d$ 以内，所以对角线下方的所有非零元素会被消完。于是就变成了这样：
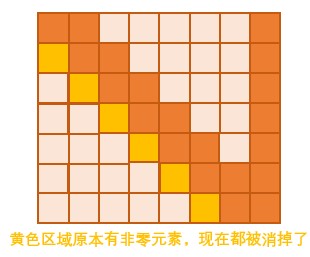(图 带状矩阵消元后)上述消元过程是 $O(nd^2)$ 的：$O(n)$ 枚举 $i$ 行，对于用每一行给下方 $d$ 行消元，每一行的消元只会枚举不超过 $d$ 个未知数。
然后发现，最后一行只剩右下角那个未知数 $x_n$，可以直接得到 $x_n$ 的解。再把 $x_n$ 的值代入到上方的式子（行）中去——我们发现上方只有 $d$ 个式子含有 $x_n$，所以只需要向上枚举 $d$ 行。
这样就可以依次求解出 $x_n,x_{n-1},\cdots,x_1$。代入复杂度 $O(nd)$。
# 演示
原矩阵
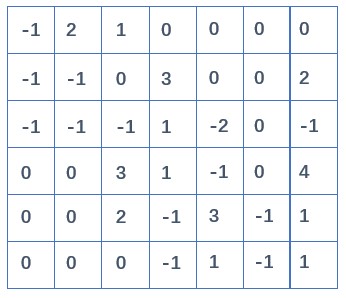
第一行 $x_1$ 系数化 1
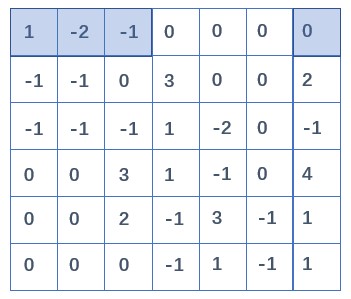
用第一行消去第二三行，使 $x_1$ 系数为 0
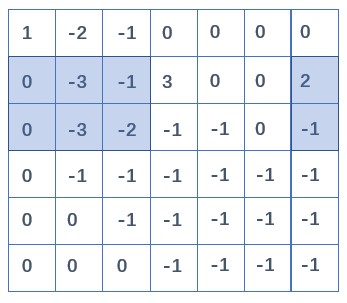
第二行 $x_2$ 系数化 1
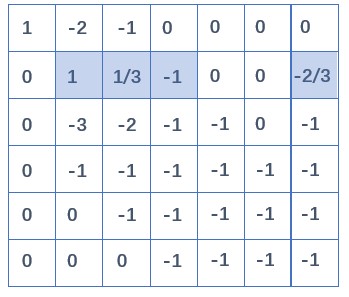
用第二行消去第三四行的 $x_2$
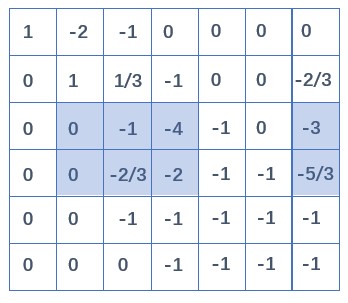
以此类推，直到消到最后一行
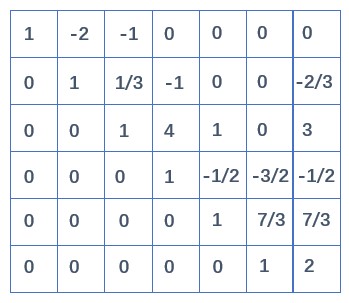
得到：
把 $x_6$ 代入到 (5)(4) 中，得到 $x_5$；把 $x_5$ 代入到 (4)(3) 中，得到 $x_4$……
（这是大概过程，都是我手玩的……如果有错不要在意）
# 例题 - Circles of Waiting (Codeforces)
这道题拿来当例题再合适不过了
- 题意
有一个点在平面直角坐标系的原点处，它每步挪动到相邻的整点处，其中有 $p_1$ 概率向左、$p_2$ 概率向下、$p_3$ 概率向右、$p_4$ 概率向下。给出整数 $R$ ，问期望多少步过后，点与原点的欧几里得距离严格大于 $R$。
数据规模：$R\le50$，$p_1+p_2+p_3+p_4=1$。
- 解析
设 $f_{x,y}$ 表示从 $(x,y)$ 处出发期望多少步后，与原点距离大于 $R$。$f_{x,y}$ 就是未知数，数量级为 $O(\pi R^2)$。
不难得到式子
如果我们把距离原点不超过 $R$ 的 $(x,y)$ 按 $x$ 为第一关键字、$y$ 为第二关键字编号为 $id_{x,y}$，可以发现：令 $d=2R+1$，则 $id_{x+1,y},id_{x-1,y},id_{x,y+1},id_{x,y-1}\in[id_{x,y}-d,id_{x,y}+d]$。
于是可以用带状矩阵做了~
> Hint. 网格图（或者平面直角坐标系）向周围移动就可以考虑这个方法
- 源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=55,MOD=1e9+7;
const int MOV[4][2]={{-1,0},{0,-1},{1,0},{0,1}};
int R,n,nid,D;
int inp[4],id[N*2+10][N*2+10],eid[N*N*4][2],p[4],mat[8000][8000];
int f[N*N*4];
int QPow(int a,int b){
int res=1;
while(b){
if(b&1) res=int(1ll*res*a%MOD);
a=int(1ll*a*a%MOD);
b>>=1;
}
return res;
}
void Gauss(int nequ,int nvar){
int equ=1,var=1;
while(equ<=nequ && var<=nvar){
if(!mat[equ][var]){printf("error\n");exit(1);}
int k=QPow(mat[equ][var],MOD-2);
for(int i=var;i<=nvar && i<=var+D;i++)
mat[equ][i]=int(1ll*mat[equ][i]*k%MOD);
mat[equ][nvar+1]=int(1ll*mat[equ][nvar+1]*k%MOD);
for(int i=equ+1;i<=equ+D && i<=nequ;i++){
if(!mat[i][var]) continue;
k=mat[i][var];
for(int j=var;j<=nvar && j<=var+D;j++)
mat[i][j]=int((mat[i][j]-1ll*mat[equ][j]*k%MOD+MOD)%MOD);
mat[i][nvar+1]=int((mat[i][nvar+1]-1ll*mat[equ][nvar+1]*k%MOD+MOD)%MOD);
}
var++;equ++;
}
}
void Calc(int nvar){
for(int i=nvar;i>=1;i--){
for(int j=i+1;j<=nvar && j<=i+D;j++){
mat[i][nvar+1]=int((mat[i][nvar+1]-1ll*mat[i][j]*f[j]%MOD+MOD)%MOD);
mat[i][j]=0;
}
f[i]=mat[i][nvar+1];
}
}
int main(){
scanf("%d",&R);
int tot=0;
for(int i=0;i<4;i++)
scanf("%d",&p[i]),tot+=p[i];
int bas=QPow(tot,MOD-2);
for(int i=0;i<4;i++)
p[i]=int(1ll*p[i]*bas%MOD);
for(int x=-R;x<=R;x++)
for(int y=-R;y<=R;y++)
if(x*x+y*y<=R*R){
id[x+N][y+N]=++nid;
eid[nid][0]=x;
eid[nid][1]=y;
}
for(int i=1;i<=nid;i++){
int x=eid[i][0],y=eid[i][1];
mat[i][i]=MOD-1;mat[i][nid+1]=MOD-1;
for(int j=0;j<4;j++){
int x_=x+MOV[j][0],y_=y+MOV[j][1];
if(id[x_+N][y_+N])
mat[i][id[x_+N][y_+N]]=p[j];
}
}
D=R*2+1;
Gauss(nid,nid);
Calc(nid);
printf("%d\n",f[id[N][N]]);
return 0;
}
|
The End
Thanks for reading!
啊？我之前还有没填的坑吗？（指没写完的博客）还是垃圾桶香啊（不是）