OI题解 - Fox Rocks(Codeforces GYM) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI题解 - Fox Rocks(Codeforces GYM)

发表于 更新于 分类于 Valine：

#听说 Lucky_Glass 博客都要日更了#（你等着，我马上就咕）

# 题意

有一个 $n$ 个点 $m$ 条边的有向图，节点编号为 $0$ 到 $n-1$，其中每条边 $u\to v$ （$u,v$ 是边的编号）满足 $0\le\left\lfloor\frac v4\right\rfloor-\left\lfloor\frac u4\right\rfloor\le1$，但是满足该条件的 $u,v$ 之间不一定有边。每条边 $u\to v$ 有权重 $w_{u\to v}$。

进行 $q$ 次询问，询问有以下类型：

  1. 给定 $x,y,k$：添加一条权重为 $k$ 的边 $x\to y$，$x,y$ 满足 $0\le\left\lfloor\frac y4\right\rfloor-\left\lfloor\frac x4\right\rfloor\le1$。（保证当前没有 $x\to y$ 这条边）
  2. 给定 $x,y$：删除边 $x\to y$。（保证当前存在 $x\to y$）
  3. 给定 $x,y$：从 $x$ 出发随机游走，到 $y$ 结束，求在 $y$ 结束的概率。其中随机游走的规则如下：若当前处于点 $u$，设 $u$ 的出边的权重之和为 $S_u$，则通过边 $u\to v$ 的概率为 $\frac{w_{u\to v}}{S_u}$。

（多组数据，不超过 $20$ 组）

数据规模：$1\le n\le50000$；$1\le m\le10^5$；$1\le q\le20000$。

# 解析

- 期望 & 动态规划

有一个比较常用的非常巧妙的转化：“求从点 $S$ 出发随机游走到点 $T$ 结束（到达后就停止移动）的概率”可以转化为“求从点 $S$ 出发随机游走到点 $T$ 结束，经过 $T$ 的期望 次数”。

正确性显然，因为最多只可能经过 $T$ 一次，那么期望就是“概率×值”，即 E(经过T的次数)=P(经过T零次)*0+P(经过T一次)*1=P(经过T一次)。

先只考虑询问——可以设计 DP，$f_i$ 表示从 $x$ 出发到达 $y$ 期望经过 $i$ 多少次，转移方程式则为：

前面的求和式很好理解，关键是 $[i=x]$。因为计算期望需要考虑所有的贡献，对于起点 $x$ 来说，经过 $x$ 可能是从另外一个点经过边到达 $x$；也可能是随机游走一开始就在起点 $x$，有一个 $1$ 的贡献，也就是 $[i=x]$。

这也算是一个套路，现学现用~

但是非常不幸的是，这张图不一定是 DAG，就不得不用高斯消元 来转移。这样复杂度就变成了 $O(n^3)$，显然不能接受，考虑优化。

- 分块

正当这时（人群中突然冒出来一个光头！）（不是），我们发现题目中：“边 $u\to v$ 只存在于满足 $0\le\left\lfloor\frac v4\right\rfloor-\left\lfloor\frac u4\right\rfloor\le1$ 的 $u,v$ 之间”。

稍加思索，我们发现可以从 $0$ 开始每四个点分成一块。环只会出现在同一个块里，如果把一个块看成一个点，整张图就变成了若干链。

这样的话，就可以对每个块做高斯消元了！块大小为 $4$，所以高斯消元也只是 $4^3$ 的。

接下来就是考虑把每一块的结果合并起来得到答案了。

- 线段树

几乎是顺理成章，倒是很像另一道题。

一个 $n$ 行 $m$ 列（$n$ 很小）的迷宫，每个位置要么是空地，要么是障碍。只能向右、上、下走。

  1. 询问从 $(u_x,u_y)$ 到 $(v_x,v_y)$ 的最少步数；
  2. 修改 $(x,y)$ 为空地/障碍。

给每个块编号，从左到右依次为 $0$ 到$\left\lceil\frac n4\right\rceil$。线段树维护区间 $[L,R]$：$d_{u,v}$ 表示从块 $L$ 的第 $u$ 个点出发，第一次到达 块 $R$ 时到达的点是 $R$ 的第 $v$ 个点的概率。

则考虑合并区间 $[L,M],[M+1,R]$，其实就是块 $M$ 和 $M+1$ 之间的转移 ——

jpg1

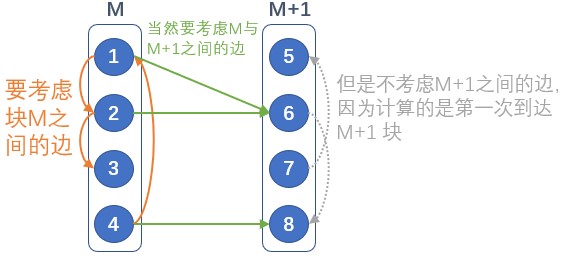
  1. 给块 $M$ 和 $M+1$ 的点重编号为 $1$ 到 $8$；
  2. 枚举 $M$ 的点 $S$ 作为起点；
  3. 按照 $f_v=\sum p_{u\to v}f_u+[v=S]$ 的规则建矩阵，高斯消元；
  4. 枚举块 $L$ 的起点 $u$，块 $M+1$ 的中继点 $t$，块 $R$ 的终点 $v$：把路径 $u\to S\to t\to v$ 统计入 d[u][v] 中。

这样就维护了线段树。

同时，我们发现修改边的操作也非常的 easy 了，只要修改点 $x$ 的出边，更新点 $x$ 的出边的权重之和，然后再 $O(\log n\times4^3)$ 让线段树递归更新 $\lfloor\frac x4\rfloor$ 即可。

那么查询呢？查询并没有要求“第一次到达 $y$ 所在块到达的点为 $y$”，因此还要做一个 $y$ 的块内的转移，计算出从 $y$ 所在块内每一个点出发，到达 $y$ 的概率。方法还是一样的。

- 漏洞

在之前的叙述中，我们默认了高斯消元是有解的，但是它真的可能无解！比如下面这张图：

jpg2

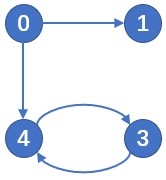
从 $0$ 出发，到达 $1$。按照我们的 DP 定义，则 $f_3=f_4=+\infty$（永远无法到达），而实际上 $f_3=f_4=0$ 才符合转移。

我们发现在高斯消元时，因为

消元时必然有一个方程被消成“没有未知数，常数项不为0”的样子，就无解了。当然也会导致算出的结果不对。其实解决方法很简单，因为方程的数量和未知数数量相等，如果有一个方程被消成没有未知数，就必然有一个未知数没有出现在方程中。

发现这种情况时，把方程改为“该未知数=0”即可。

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=50000,TN=N/4;
const double EPS=1e-9;

int cas,n,m,q;
int tot[N+3],Ein[N][4],Eout[N][4];

struct NODE{
    int le,ri;
    double num[4][4];
    NODE(){}
    NODE(int lef,int rig){
        le=lef;ri=rig;
        for(int i=0;i<4;i++)
            for(int j=0;j<4;j++)
                num[i][j]=0;
    }
};

double mat[10][10];
namespace GAUSS{
    double LABS(double num){return num<0? -num:num;}
    int Gauss(int nvar,int nequ){
        int var=1,equ=1;
        while(var<=nvar && equ<=nequ){
            int mxe=equ;
            for(int i=equ+1;i<=nequ;i++)
                if(LABS(mat[mxe][var])<LABS(mat[i][var]))
                    mxe=i;
            for(int i=var;i<=nvar+1;i++)
                swap(mat[mxe][i],mat[equ][i]);
            if(LABS(mat[equ][var])<EPS){
                for(int i=var;i<=nvar+1;i++)
                    mat[equ][i]=0;
                mat[equ][var]=1;
            }
            double k=mat[equ][var];
            for(int i=var;i<=nvar+1;i++)
                mat[equ][i]/=k;
            for(int i=1;i<=nequ;i++){
                if(i==equ || LABS(mat[i][var])<EPS) continue;
                k=mat[i][var];
                for(int j=var;j<=nvar+1;j++)
                    mat[i][j]-=mat[equ][j]*k;
            }
            var++;equ++;
        }
        return 1;
    }
    void Clear(int nvar,int nequ){
        for(int i=1;i<=nequ;i++)
            for(int j=1;j<=nvar+1;j++)
                mat[i][j]=0;
    }
};

NODE Merge(const NODE &A,const NODE &B){
    NODE res(A.le,B.ri);
    int lef=A.ri;
    for(int S=lef*4;S<lef*4+4;S++){
        GAUSS::Clear(8,8);
        mat[S-lef*4+1][9]=-1;
        for(int i=1;i<=8;i++) mat[i][i]--;
        for(int u=lef*4;u<lef*4+4;u++){
            for(int i=0;i<4;i++){
                if(!tot[u]) continue;
                double Pin=(double)Ein[u][i]/tot[u],Pout=(double)Eout[u][i]/tot[u];
                mat[i+1][u-lef*4+1]+=Pin;
                mat[i+5][u-lef*4+1]+=Pout;
            }
        }
        int xx=GAUSS::Gauss(8,8);
        if(xx<0) printf("warning %d! ([%d,%d]+[%d,%d]) S=%d\n",xx,A.le,A.ri,B.le,B.ri,S);
        // printf("\n");
        // for(int i=1;i<=8;i++){
            //     for(int j=1;j<=9;j++)
            //         printf("%f ",mat[i][j]);
            //     printf("\n");
            // }
        double ans[4]={};
        for(int i=0;i<4;i++)
            ans[i]=mat[i+5][9];
        // if(lef==1){
        //     printf("%d:\n",S);
        //     for(int i=0;i<4;i++)
        //         printf(" %f",ans[i]);
        //     printf("\n");
        //     if(S==4) printf("%f*%f*%f\n",A.num[0][S],)
        // }
        for(int p1=0;p1<4;p1++)
            for(int p2=0;p2<4;p2++)
                for(int p3=0;p3<4;p3++)
                    res.num[p1][p2]+=A.num[p1][S%4]*ans[p3]*B.num[p3][p2];
    }
    return res;
}
double Single(int S,int T){
    GAUSS::Clear(4,4);
    mat[S%4+1][5]--;
    int es=S/4*4;
    for(int u=es;u<es+4;u++){
        mat[u-es+1][u-es+1]--;
        if(u==T || !tot[u]) continue;
        for(int i=0;i<4;i++){
            mat[i+1][u-es+1]+=(double)Ein[u][i]/tot[u];
        }
    }
    // printf("\n");
    // for(int i=1;i<=4;i++){
    //     for(int j=1;j<=5;j++)
    //         printf("%f ",mat[i][j]);
    //     printf("\n");
    // }
    GAUSS::Gauss(4,4);
    return mat[T-es+1][5];
}
struct SEGTREE{
    NODE nod[TN*2+10];
    int idx(int lef,int rig){return (lef+rig)|(lef!=rig);}
    void Build(int lef,int rig){
        int u=idx(lef+1,rig+1);
        nod[u].le=lef;nod[u].ri=rig;
        if(lef==rig){
            for(int i=0;i<4;i++)
                for(int j=0;j<4;j++)
                    nod[u].num[i][j]=i==j;
            return;
        }
        int mid=(lef+rig)>>1;
        Build(lef,mid);Build(mid+1,rig);
        nod[u]=Merge(nod[idx(lef+1,mid+1)],nod[idx(mid+2,rig+1)]);
    }
    void Update(int lef,int rig,int pos){
        if(lef==rig) return;
        int mid=(lef+rig)>>1;
        if(pos<=mid) Update(lef,mid,pos);
        else Update(mid+1,rig,pos);
        nod[idx(lef+1,rig+1)]=Merge(nod[idx(lef+1,mid+1)],nod[idx(mid+2,rig+1)]);
    }
    NODE Query(int lef,int rig,int Le,int Ri){
        if(Le<=lef && rig<=Ri) return nod[idx(lef+1,rig+1)];
        int mid=(lef+rig)>>1;
        if(Ri<=mid) return Query(lef,mid,Le,Ri);
        if(mid<Le) return Query(mid+1,rig,Le,Ri);
        return Merge(Query(lef,mid,Le,Ri),Query(mid+1,rig,Le,Ri));
    }
};
SEGTREE Se;

void Clear(){
    for(int i=0;i<n;i++) tot[i]=0;
    for(int i=0;i<n;i++)
        for(int v=0;v<4;v++)
            Ein[i][v]=Eout[i][v]=0;
}
int main(){
    // freopen("input.txt","r",stdin);
    // freopen("output.txt","w",stdout);
    scanf("%d",&cas);
    for(int ca=1;ca<=cas;ca++){
        scanf("%d%d%d",&n,&m,&q);
        if(n%4) n=(n/4+1)*4;
        Clear();
        for(int i=1,u,v,num;i<=m;i++){
            scanf("%d%d%d",&u,&v,&num);
            tot[u]+=num;
            if(u/4==v/4) Ein[u][v%4]=num;
            else Eout[u][v%4]=num;
        }
        Se.Build(0,n/4-1);
        printf("Case #%d:",ca);
        while(q--){
            int cmd;scanf("%d",&cmd);
            switch(cmd){
                case 1:{
                    int u,v,num;scanf("%d%d%d",&u,&v,&num);
                    tot[u]+=num;
                    if(u/4==v/4) Ein[u][v%4]=num;
                    else Eout[u][v%4]=num;
                    Se.Update(0,n/4-1,u/4);
                    break;
                }
                case 2:{
                    int u,v;scanf("%d%d",&u,&v);
                    if(u/4==v/4) tot[u]-=Ein[u][v%4],Ein[u][v%4]=0;
                    else tot[u]-=Eout[u][v%4],Eout[u][v%4]=0;
                    Se.Update(0,n/4-1,u/4);
                    break;
                }
                case 3:{
                    int u,v;scanf("%d%d",&u,&v);
                    if(u/4>v/4) {printf(" %.6f",0.0);break;}
                    NODE res=Se.Query(0,n/4-1,u/4,v/4);
                    // for(int i=0;i<4;i++)
                    //     for(int j=0;j<4;j++){
                    //         printf("%f ",res.num[i][j]);
                    //         if(j==3) printf("\n");
                    //     }
                    double ans=0;
                    for(int S=v/4*4;S<v/4*4+4;S++){
                        if(S==v) ans+=res.num[u%4][v%4];
                        else ans+=res.num[u%4][S%4]*Single(S,v);
                    }
                    printf(" %.6f",ans);
                    break;
                }
            }
        }
        printf("\n");
    }
    return 0;
}

The End

Thanks for reading!

不知道“我马上就咕”这句话会不会被咕掉 : )