#还真就日更博客了呗# (犹豫地)打开了新世界的大门
# 前言
计算几何不常考,然后只要碰到几何题就咕掉 awa……这次省选模拟极其爆炸,用初中学的计算几何来推一个式子,最后错了(心态爆炸)。然后发现标程写的代码及其简洁,看出来了用了向量的相关知识。
对于向量只知道加减、数乘、平面向量基本定理的我再也忍不下去了…… Hello OI-wiki!
# 向量的坐标表示
OI 中一般不会给你一个抽象的向量让你来解题,而是在一个直角坐标系 的背景下用向量来作出判断。
其实很好理解,因为向量具有方向和长度(大小),在平面内是可以随意移动的。因此对于向量 $\overrightarrow{AB}$,我们将它平移,使得 $A$ 点落于坐标原点,就可以用 $B$ 的坐标表示:$\overrightarrow{AB}=(x_B,y_B)$。
那么可以得到一些线性计算基本的性质,设向量 $\mathbf a=(x,y),\mathbf b=(p,q)$:
- $\mathbf a+\mathbf b=(x+p,y+q)$;
- $\mathbf a-\mathbf b=(x-p,y-q)$;
- $\mu\mathbf a=(\mu x,\mu y)$;
# 向量的点积(数量积)
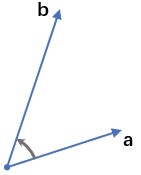
$\langle \mathbf{a,b}\rangle$ 表示 $\mathbf{a,b}$ 的夹角,如图:
对于向量 $\mathbf{a,b}$,定义 $\mathbf a$ 和 $\mathbf b$ 的点积 $\mathbf a\cdot\mathbf b=|\mathbf a|\cdot|\mathbf b|\cdot\cos\langle \mathbf{a,b}\rangle$。
有了点积,向量在 OI 中的应用又多了一些了:
- $\mathbf a\cdot\mathbf b=\pm|\mathbf a||\mathbf b|\Leftrightarrow\mathbf{a,b}\text{共线}$,因为 ;(同向/反向,但是似乎 OI 中并不在意向量的方向)
- $\mathbf a\cdot\mathbf b=0\Leftrightarrow\mathbf{a,b}\text{垂直}$;
- 求 $\mathbf{a,b}$ 的夹角:$\cos\langle\mathbf{a,b}\rangle=\frac{\mathbf a\cdot\mathbf b}{|\mathbf a||\mathbf b|}$。
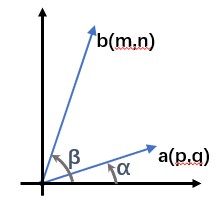
当然,点积也可以用坐标计算—— $\mathbf a=(p,q),\mathbf b=(m,n)$,则 $\mathbf a\cdot\mathbf b=(mp+nq)$。
> 推导
- $\mathbf a\cdot\mathbf b=|\mathbf a||\mathbf b|\cos(\beta-\alpha)=|\mathbf a||\mathbf b|(\cos\beta\cos\alpha+\sin\beta\sin\alpha)$
- $\cos\alpha=\frac{p}{|\mathbf a|},\sin\alpha=\frac q{|\mathbf a|},\cos\beta=\frac m{|\mathbf b|},\sin\beta=\frac n{|\mathbf b|}$
- 代入可得
# 向量的叉积
(这里只讲对 OI 有用的 awa)同一平面内 $\mathbf a$ 与 $\mathbf b$ 的叉积记作 $\mathbf a\times\mathbf b$,满足 $|\mathbf a\times\mathbf b|=|\mathbf a||\mathbf b||\sin\langle\mathbf {a,b}\rangle|$(注意绝对值)。画个图稍微观察一下,发现 $|\mathbf a\times\mathbf b|$ 就是以 $\mathbf {a,b}$ 为一组邻边的平行四边形的面积:
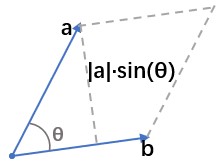
当然除以 $2$ 也可以算三角形面积~
同样,向量叉积可以用坐标表示:$\mathbf a=(p,q),\mathbf b=(m,n)$,则 $|\mathbf a\times\mathbf b|=np-mq$。
推导差不多,就是把 $\sin(\beta-\alpha)$ 展开成 $\sin\beta\cos\alpha-\cos\beta\sin\alpha$。
叉积还有另外一个用处——判断点在有向 直线的左侧还是右侧(怎么理解“有向”:你可以把该直线的正方向当作“前方”,然后分左右)。这就要提到叉积的“右手定则”了—— $\mathbf a\times\mathbf b$ 是一个向量,其方向垂直于 $\mathbf {a,b}$ 所在平面,竖直方向上的坐标为 $(|\mathbf a||\mathbf b|\sin\langle\mathbf{a,b}\rangle)$(注意 $\sin$ 没有绝对值),方向可以用右手定则判断:
> 右手定则:
- (右手)四指并拢指向 $\mathbf a$ 的方向;
- 四指弯向 $\mathbf b$;
- 拇指方向为 $\mathbf a\times\mathbf b$ 的方向。
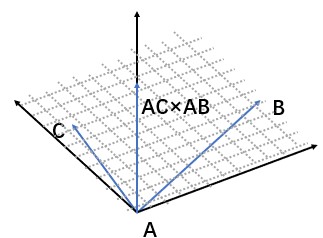
假设要判断 $C$ 在直线 $AB$ 的哪一侧(以 $B$ 为前方),则计算 $\overrightarrow{AB}\times\overrightarrow{AC}$ 的竖直方向坐标 $z$:如果 $z<0$,则 $C$ 在 $AB$ 的右侧,否则在左侧。如图展示了 $C$ 在 $AB$ 左边的情况:
The End
Thanks for reading!
心情好多了呢~