学习笔记 - 析合树 | Lucky

啃不到 WC 课件 (QwQ) 就去啃 OIWiki 系列

# 引入

“不管什么问题，中国人都能设计出一个数据结构来做……” - Codeforces 某外国用户的评论

（咳咳，非常真实）没错，析合树就是用来解决这样一个特殊的问题的——

给出一个 1 到 n 的排列 $A$，当下标区间 $[l,r]$ 满足 $A_l$ 到 $A_r$ 的值域是连续的，定义 $[l,r]$ 是“连续段”。
① 求总共有多少个连续段；
② 求包含区间 $[l,r]$ 的最小的连续段；

举个例子：
1 4 2 3 5 6 中 $[2,5]$ 是一个连续段，因为这段数中出现了 2 到 5 的所有数。

析合树就是用来解决这个问题的一个非在线算法（至少一般的析合树不能在线），我的意思是不能动态在排列末尾添加元素，也不能删除元素。

# 理论

（听说 WC 课件讲的很玄乎，那我还是用比较简单的语言来解释一下）

- 连续段&本原段

连续段就是上面 # 引入中的定义了。在此基础上定义满足以下条件的 $[l,r]$ 为本原段：

$[l,r]$ 是连续段；
不存在连续段 $[l’,r’]$ 使得 $[l’,r’]$ 与 $[l,r]$ 有交集且 $[l,r]$ 和 $[l’,r’]$ 不是包含、被包含的关系；

关于连续段有一些性质，若 $A=[l,r],B=[l’,r’]$ 都是连续段（下面把区间的并、交看成集合就好了）：

$A\cup B$ 和 $A\cap B$ 都是连续段；
如果 $A\not\in B$ 且 $B\not\in A$，则$\{i|i\in A\text 且i\not\in B\}$ 和 $\{i|i\in B\text 且i\not\in A\}$ 都是连续段；

其实都比较简单。

因为本原段是特殊的连续段，所以它的值域也是连续的，因此我们可以用值域范围来表示一个本原段：
比如 $A=\{3,2,4,5,1\}$ 的 $[1,3]$ 就是一个本原段，它也可以用 $<2,4>$ 表示。

这里注意区分本篇博客中的 $[l,r]$ 和 $< l,r >$。
$[l,r]$ 表示下标从 $l$ 到 $r$，$< l,r >$ 表示数值从 $l$ 到 $r$。

- 析点&合点

根据本原段的定义，两个不相等的本原段要么为包含关系，要么是相离关系。这样的区间是可以用树形结构存储的——析合树的每个节点都是一个本原段，且每个本原段都出现在析合树上，如果本原段 $B\in A$，则 $B$ 是 $A$ 的儿子。

不难发现整个区间 $[1,n]$ 就是一个本原段，因此 $[1,n]$ 是析合树的根。

下面对于析合树上的任意一个点 $u$ 给出一些定义：

儿子序列：$u$ 的儿子按下标从小到大排列得到的序列 $P_u$；
儿子排列：$u$ 的儿子序列的每个元素都用它的值域左端点表示，然后离散化得到的序列（当然是一个排列）
比如这样，假设儿子序列为 $\{<1,2>,<4,7>,<3,3>\}$
那么把它用值域区间左端点表示为 $\{1,4,3\}$
然后离散化为 $\{1,3,2\}$
合点：如果点 $u$ 的儿子排列单调递增或单调递减，则称 $u$ 为合点；
此外，析合树的叶子节点的儿子排列为空，也认为叶子节点是合点。
析点：析合树上不是合点的点。

合点的性质非常显然。它应该是一段连续的递减或者递增的区间，也就是说：
如果 $< l,r >$ 是一个合点，则这段数是 $\{l,l+1,\cdots,r-1,r\}$ 或 $\{r,r-1,\cdots,l+1,l\}$。

析点的性质需要解释一下。任何一个析点的儿子序列中，不存在任何长度超过 1 的真子区间使得该子区间的所有儿子能够合成一个连续段（这里的“长度大于 1”指的是在儿子序列中的长度）。这就和析合树的定义有关系了，简单证明一下：

假设 $u$ 的儿子序列 $P_u=\{v_1,v_2,v_3,\cdots,v_t\}$ 中有一段最长的子区间（长度大于 1） $[l,r]=\{v_l,v_{l+1},\cdots,v_r\}$ 满足 $\bigcup_{i=l}^rv_i$ 为一个连续段。那么 $\bigcup_{i=l}^rv_i$ 为一个本原段！因为它是 $P_u$ 中最长的一个子区间，所以没有其他连续段和它相交且不包含。但是 $\bigcup_{i=l}^rv_i$ 这个本原段本身并没有出现在析合树上，不符合析合树的定义“每个本原段都出现在析合树上”。

# 栗子

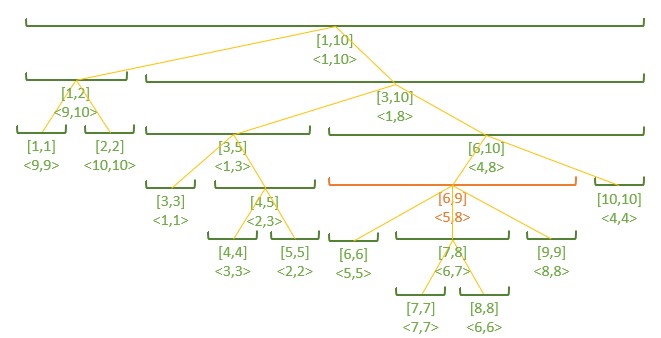
原排列为 $\{9,10,1,3,2,5,7,6,8,4\}$。

于是构造出析合树长这样（绿色是合点，橙色是析点）：

# 增量法

- 大致流程

假设已经建出了前 $i-1$ 个位置的析合森林，并且用一个栈存储了这些树的根（栈中的元素是按左端点下标排序的，也就是说栈顶的左端点的下标是最大的，也就是包含第 $i-1$ 个位置），现在要把第 $i$ 个位置插入进去。

设现在要合并的点是 cur。

如果 cur 能作为栈顶点 top 的儿子，就直接把 cur 连为 top 的儿子，然后弹出 top 并把 top 作为新的 cur 继续参与合并；
如果不能作为 top 的儿子，就看能否把从栈顶开始的连续一段点 和 cur 连成一棵树（新建一个根，这些点都能作为这个根的儿子），如果可以，连为一棵树，树根作为新的 cur 继续合并；
直到栈空或者以上两个条件都不满足，然后把 cur 插入栈中。

- 需要维护的变量

先预处理一个 RMQ，计算原排列中任意区间的最大值、最小值。

当要增量法插入位置 $i$ 时：

用两个单调栈：分别维护 $[1\text~i,i]$ 的最小值和最大值；
用线段树：维护 $j\in[left,right]$ 中 $\left[\max_{k\in[j,i]}A_k-\min_{k\in[j,i]}A_k-(i-j)\right]$ 的最小值；

对于析合树的每个点 $u$ 维护：

$u$ 表示的本原段的左右端点；
$u$ 的所有儿子的最大的左端点（其实就是最后插入到 $u$ 的儿子的左端点）；
$u$ 是合点还是析点；

- 如何维护

RMQ 很简单，就不细说了，实现可以参考我在代码中写的 struct RMQ。

维护单调栈是比较一般的操作，拿维护最大值举例：把栈顶元素的大小与 $A_i$ 比较，如果比 $A_i$ 小，就弹出，直到栈空或者栈顶比 $A_i$ 大。最后把 $i$ 插入单调栈——没错，单调栈里维护的是下标——因为维护单调栈的根本目的是维护线段树！

仍然拿维护最大值举例，称栈顶元素为 X，栈顶元素的后一个元素是 Y。如果 $A_X<A_i$，那么 $A_X$ 被弹出，意味着 $[p,i]$ ($p\in[Y+1,X]$) 这段区间的最大值不再是 $A_X$，于是在线段树中把 $A_X$ 的贡献减去，即把线段树中 $[Y+1,X]$ 区间减去 $A_X$。

设结束时栈顶元素为 X（如果为空，那 X=0），那么 $[p,i]$ ($p\in[X+1,i]$) 这些区间的最大值是 $A_i$，把 $A_i$ 的贡献加入线段树，即 $[X+1,i]$ 区间加。

最小值的单调栈同理。

当我们完成 $i$ 位置的增量后，i++，此时线段树要更新，即 $[1,i]$ 区间减 $1$。

析合树的相关维护下面讲。

- 插入位置 $i$

终于到重点了……

我们先计算出最小的 $L$，使得 $[L,i]$ 能够作为一个连续段。如何计算？这时候线段树就发挥作用了：
一个连续段 $[j,i]$ 一定满足 $\max_{k\in[j,i]}A_k-\min_{k\in[j,i]}A_k=i-j$；
又因为 $A$ 是一个排列，那么 $\max_{k\in[j,i]}A_k-\min_{k\in[j,i]}A_k-(i-j)\ge0$。

那么就是要计算满足 $\max_{k\in[j,i]}A_k-\min_{k\in[j,i]}A_k-(i-j)=0$ 的最小 $j$。这个用线段树计算就可以了。求出的最小 $j$ 就是 $L$。

方便叙述，下面把析合树的点 $u$ 代表的本原段记为 $[u_l,u_r]$。

设 cur 是当前要插入析合树森林的点。cur 的初始值为 $[i,i]$。

分几种情况：

$l_{top}<L$：那么根据 $L$ 的定义，cur 和 top 肯定不能合并，于是插入完毕，推出循环；
top 是合点，而且 top 的最后一个儿子能够和 cur 合并（这说明了 cur 作为 top 的儿子后，top 仍然是合点），就把 cur 作为 top 的儿子，并且更新 top 的信息（包括本原段、最后一个儿子）。

把 top 弹出作为新的 cur。
（在不满足 2. 的时候）如果 top 所表示的本原段可以和 cur 表示的本原段合成一个新的本原段，直接把两个点的本原段合成一个新的合点 now，并把 top 和 cur 都作为 now 的儿子；把 top 弹栈，然后把 now 作为新的 cur。

根据之前推导的析点的性质：析点中任意两个相邻的儿子合起来不能构成一个连续段。
但是情况 3. 中 now 已经存在相邻的儿子 top,cur，所以 now 是合点。
（在不满足 3. 的时候）把栈中左端点大于等于 $L$ （之前线段树计算的 $L$，还记得吗？）的所有点与 cur 合成一个新的析点 now，这些点都作为 now 的儿子；然后把 now 作为新的 cur。

仍然用析点的那个性质证明 now 是析点：

首先栈中存储的是析合树森林的根，而两个相邻的根肯定是不能合成新的连续段的（不然两个根就会在增量的时候合成一个新的点了），而且 cur 和 top 不能合成新的本原段，所以 now 的任意两个相邻的儿子都不能合成一个连续段。

所以 now 满足析点性质，是析点。

最后得到的 cur 作为析合树森林的一个根入栈。

- 结果

经过上述步骤，终于建出一个析合树了——析合树的根就是最后剩在栈里的一个点。

最后栈一定会只剩一个点，因为 $[1,n]$ 整个区间就是一个本原段，应作为整棵树的根。

可以参考一下代码？

# 一些（一个）小技巧

毕竟析合树是一棵树嘛，就可以用一些树的惯用伎俩……比如 LCA。

根据析合树的定义，父节点表示的本原段一定包含子树中的节点的本原段。因此求析合树上两个点 u,v 的 LCA 就是求同时包含 $[u_l,u_r]$ 和 $[v_l,v_r]$ 的最小的本原段。

# 源代码的题目是“求包含区间 $[l,r]$ 的最小的连续段”。因为本原段是连续的一个区间，所以包含区间 $[l,r]$ 只要分别包含 $[l,l]$ 和 $[r,r]$ 就好了~ 于是我们可以在增量的时候额外存储一个节点数组 rt[i] ：表示的本原段为 $[i,i]$ 的点，然后每次询问就 $O(\log n)$ 求一下 rt[l],rt[r] 的 LCA 就好了。

顺便一提，析合树的树深是 $O(n)$，节点数要开 $2n$。

# 源代码

给出一个 1 到 n 的排列，进行 m 次询问：每次询问求包含区间 $[l,r]$ 的最小的连续段。

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e5*2;

int n,m;
/*
1. num[i] 原数组
2. id[i] 原数组第 i个位置对应析合树哪个点
3. tlef[i] 析合树上的点 i 对应的下标区间左端点
4. trig[i] 析合树上的点 i 对应的下标区间右端点
5. dep[i] 析合树上的点 i 的深度
6. pre[i][k] 析合树上的点 i 的祖先的倍增数组（求LCA）
7. typ[i] 若 =true 析合树上的点 i 是合点；=false 为析点
8. las[i] 表示析合树的点 i 的最后一个儿子的左端点
*/
int num[N+3],id[N+3],tlef[N+3],trig[N+3],dep[N+3],pre[N+3][20],las[N+3];
bool typ[N+3];

//手写栈
struct STACK{
    int idx[N+3],head;
    void Pop(){head--;}
    void Clear(){head=0;}
    int Top(int i=0){return idx[head-i];}
    void Push(int val){idx[++head]=val;}
    bool Empty(){return !head;}
};
/*
设现在增量法正在处理位置 i
> Smx,Smn 分别维护从 1 到 i 的单调递减、单调递增序列（一定包含 i）
> Stre 维护了现在的析合树森林的根
*/
STACK Smx,Smn,Stre;

//预处理原数组 num 区间最大值最小值
struct RMQ{
    int lg2[N+3],mn[N+3][20],mx[N+3][20];
    void Build(){
        lg2[1]=0;
        //Hint. lg2[] 向下取整
        for(int i=2;i<=n;i++) lg2[i]=lg2[i>>1]+1;
        for(int i=1;i<=n;i++) mn[i][0]=mx[i][0]=num[i];
        for(int i=1;i<20;i++)
            for(int j=1;j+(1<<i)-1<=n;j++)
                mn[j][i]=min(mn[j][i-1],mn[j+(1<<(i-1))][i-1]),
                mx[j][i]=max(mx[j][i-1],mx[j+(1<<(i-1))][i-1]);
    }
    int Min(int lef,int rig){
        int _lg=lg2[rig-lef+1];
        return min(mn[lef][_lg],mn[rig-(1<<_lg)+1][_lg]);
    }
    int Max(int lef,int rig){
        int _lg=lg2[rig-lef+1];
        return max(mx[lef][_lg],mx[rig-(1<<_lg)+1][_lg]);
    }
};
RMQ Rm;

//线段树维护 max[l,r]-min[l,r]-(r-l) 的最小值
struct SEG{
    int mn[N*2],addt[N*2];
    void PushUp(int u){mn[u]=min(mn[u<<1],mn[u<<1|1]);}
    void PushDown(int u){
        if(addt[u]){
            addt[u<<1]+=addt[u];
            addt[u<<1|1]+=addt[u];
            mn[u<<1]+=addt[u];
            mn[u<<1|1]+=addt[u];
            addt[u]=0;
        }
    }
    void Modify(int u,int lef,int rig,int Le,int Ri,int val){
        if(rig<Le || Ri<lef) return;
        if(Le<=lef && rig<=Ri){
            mn[u]+=val;addt[u]+=val;
            return;
        }
        PushDown(u);
        int mid=(lef+rig)>>1;
        Modify(u<<1,lef,mid,Le,Ri,val);
        Modify(u<<1|1,mid+1,rig,Le,Ri,val);
        PushUp(u);
    }
    int Query(int u,int lef,int rig){
        if(lef==rig) return lef;
        PushDown(u);
        int mid=(lef+rig)>>1;
        if(!mn[u<<1]) return Query(u<<1,lef,mid);
        else return Query(u<<1|1,mid+1,rig);
    }
};
SEG Se;

//储存析合树的邻接表
struct EDGE{
    int to;EDGE *nxt;
    EDGE(){}
    EDGE(int _t,EDGE *_n):to(_t),nxt(_n){}
};
struct TREE{
    EDGE Ed[N*2],*ncnt,*head[N+3];
    TREE(){ncnt=Ed;}
    void AddEdge(int u,int v){
        EDGE *now=++ncnt;
        *now=EDGE(v,head[u]);
        head[u]=now;
    }
    EDGE*& operator [](int i){return head[i];}
};
TREE Tr;
int tcnt,root;
/*
> tcnt 析合树的点的数量（用于新建点）
> root 析合树的根
*/

//判断下标区间 [lef,rig] 能否作为一个连续区间
bool Judge(int lef,int rig){return Rm.Max(lef,rig)-Rm.Min(lef,rig)==rig-lef;}
//建析合树
void Build(){
    for(int i=1;i<=n;i++){
        // 1. 维护单增、单减区间；顺便维护线段树
        /*Hint. Smn,Smx 都是存储的数组下标*/
        while(!Smn.Empty() && num[i]<=num[Smn.Top()]){
            /*
            [Smn.Top(1)+1,i] 这一段的 min 不再是 num[Smn,Top()]，
            在线段树中减去贡献（原贡献为 -num[Smn.Top()]）
            */
            Se.Modify(1,1,n,Smn.Top(1)+1,Smn.Top(),num[Smn.Top()]);
            Smn.Pop();
        }
        while(!Smx.Empty() && num[i]>=num[Smx.Top()]){
            //同理
            Se.Modify(1,1,n,Smx.Top(1)+1,Smx.Top(),-num[Smx.Top()]);
            Smx.Pop();
        }
        //现在 [ Smn.Top() ~ i , i ] 的最小值是 num[i]，[ Smx.Top() ~ i , i ] 的最大值是 num[i]
        //计算 i 对线段树节点的贡献
        Se.Modify(1,1,n,Smn.Top()+1,i,-num[i]);
        Se.Modify(1,1,n,Smx.Top()+1,i,num[i]);
        Smn.Push(i);Smx.Push(i);

        // 2. 插入节点 i
        int cur=++tcnt; //新建点表示 [i,i]
        id[i]=cur;tlef[cur]=trig[cur]=i;
        int Le=Se.Query(1,1,n); //计算出最小的 Le 使得 [Le,i] 有可能合为一个区间
        while(!Stre.Empty() && tlef[Stre.Top()]>=Le){
            // 如果栈顶是合点，且 cur 能够作为它的儿子
            if(typ[Stre.Top()] && Judge(las[Stre.Top()],i)){
                /* Hint. 这个情况是“把 cur 作为儿子过后仍然是合点”
                         因此不仅要保证整个区间能够连成一块
                         还要保证最后一个儿子和 cur 能够合成一块
                */
                //那么栈顶仍然是合点
                las[Stre.Top()]=tlef[cur]; //更新最后一个儿子的左端点（也可以不更新，只是这样符合定义）
                trig[Stre.Top()]=i; //更新点所表示的区间
                Tr.AddEdge(Stre.Top(),cur); //连边
                cur=Stre.Top();Stre.Pop(); //将栈顶弹出，作为新的 cur
            }
            else if(Judge(tlef[Stre.Top()],i)){
                //因为出现了连续的两个儿子能够连成一个区间，一定是合点
                typ[++tcnt]=true;
                tlef[tcnt]=tlef[Stre.Top()]; //计算左右端点
                trig[tcnt]=i;
                las[tcnt]=tlef[cur]; //存储最后一个儿子的左端点
                Tr.AddEdge(tcnt,Stre.Top());Stre.Pop(); //连边
                Tr.AddEdge(tcnt,cur);
                cur=tcnt; //合成的点作为新的 cur 继续合成
            }
            else{
                // 因为没有任何两个相邻的点能够合成一块，所以是个析点
                Tr.AddEdge(++tcnt,cur);
                do{
                    Tr.AddEdge(tcnt,Stre.Top());
                    Stre.Pop();
                }while(!Stre.Empty() && !Judge(tlef[Stre.Top()],i));
                //把所有能连的点都连上
                tlef[tcnt]=tlef[Stre.Top()];
                trig[tcnt]=i;
                Tr.AddEdge(tcnt,Stre.Top());Stre.Pop();
                //最后一个点单独处理，要用来更新右区间
                cur=tcnt; //作为新的 cur 参与合成
            }
        }
        //合成结束，把当前点插入析合树森林
        Stre.Push(cur);
        Se.Modify(1,1,n,1,i,-1); //计算下一个点时 i++，线段树的每个节点都会 -1（具体可以去看线段树的定义）
    }
    //整个区间一定是连续段，于是只会留下一个点
    //这个点就是析合树的根节点
    root=Stre.Top();
}
//在析合树上 DFS 获取 dep 和 倍增数组
void DFS(int u){
    // printf("! %d\n",u);
    for(int i=1;i<20;i++)
        pre[u][i]=pre[pre[u][i-1]][i-1];
    for(EDGE *it=Tr[u];it;it=it->nxt){
        int v=it->to;
        dep[v]=dep[u]+1;
        pre[v][0]=u;
        DFS(v);
    }
}
//求析合树上点u,v的 LCA
int LCA(int u,int v){
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=19;i>=0;i--)
        if(dep[pre[u][i]]>=dep[v])
            u=pre[u][i];
    if(u==v) return v;
    for(int i=19;i>=0;i--)
        if(pre[u][i]!=pre[v][i]){
            u=pre[u][i];
            v=pre[v][i];
        }
    return pre[u][0];
}
//求析合树上的点 u 向上跳 dis 步得到的点
int Move(int u,int dis){
    for(int i=19;i>=0;i--)
        if(dis>>i&1)
            u=pre[u][i];
    return u;
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&num[i]);
    Rm.Build();
    Build();
    DFS(root);
    scanf("%d",&m);
    for(int i=1;i<=m;i++){
        int ql,qr;scanf("%d%d",&ql,&qr);
        //要同时包含 [ql,ql] [qr,qr]，就是要求这两个区间对应的点的 LCA
        ql=id[ql];qr=id[qr];
        int lca=LCA(ql,qr);
        if(typ[lca])
            printf("%d %d\n",tlef[Move(ql,dep[ql]-dep[lca]-1)],trig[Move(qr,dep[qr]-dep[lca]-1)]);
        else
            printf("%d %d\n",tlef[lca],trig[lca]);
    }
    return 0;
}

The End

Thanks for reading!

这是真的要期末考试了 awa
Upd. 写完这篇博客的时候期末考完了 awa