OI题解 - Count Subsequences(Codechef) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI题解 - Count Subsequences(Codechef)

发表于 更新于 分类于 Valine：

什么时候信息竞赛也要期末考试了……
第一场的难度顺序好像不大对劲，把 T1T3 AC 了然后 T2 爆零 qwq

# 题面

> Codechef传送门

如果一个整数序列的各元素之和可以被给定整数 $K$ 整除，则称这个序列是好的。给定整数序列 $A_1,A_2,…,A_N$。Hasan想计算该序列有多少子序列是好的。不过这样的话问题就太简单了，因此Hasan决定再加一个限制。

任意非空下标序列 $i_1< i_2< \cdots < i_L$对应子序列$A_{i_1}, A_{i_2},…, A_{i_L}$。如果满足 $i_L-i_1\ge W$，则称这个子序列非常好。请帮Hasan统计非常好的子序列方案数。由于答案可能非常大，请输出方案数对$10^9+7$ 取模的结果。

（多组数据，每个数据点包含 $T$ 组数据）

数据规模：
- $1\le T\le1000$；
- $1\le N\le 10^5$，$0\le W\le N-1$；
- $0\le A_i\le K-1$，$2\le K\le50$；
- 每个数据点中的所有 $N$ 之和不超过 $3\times 10^5$；

# 解析

如果没有 $W$ 的限制，这道题是一道非常简单的 DP，类似于背包。大概也不需要说了。

考虑在 $W$ 的限制下怎样求答案。首先我们固定所选子序列的左端点（最左边元素）位置为 $L$，那么就必须要在 $[L+W,N]$ 这段区间内选择至少一个元素。最后把所有位置作为 $L=1\text~N$ 对应答案求和就可以了，不难发现因为每一次固定的左端点不同，所以这样求和得到的方案数不重不漏。

假设现在确定了 $L$，怎样计算方案数？
设计 DP 状态 f[i][j] 表示已经在 $A_{L+1}\text~A_i$ 这些元素中选取了一些元素，且元素之和模 $K$ 余 $j$ 的方案数。那么下面的转移应该很好理解：

啊哈？
然后方案数就是“在 $A_{L+1}\text~A_N$ 中选取的元素之和被 $K$ 整除的方案数”-“在 $A_{L+1}\text~A_{L+W-1}$ 中选取的元素之和被 $K$ 整除的方案数”（这样减了就可以保证一定在 $A_{L+W}\text~A_N$ 中选取了至少一个元素了）。

但是不可能枚举 $L$ 然后每个都分别计算。

于是题解中所说的分治是这样的：定义“询问区间”为 $[L,L+W]$。从初始区间 $[1,N]$ 开始，求解每个被包含在当前区间中的询问区间 的答案；设当前区间为 $[left,right]$ 定义 $mid$ 为区间中点，递归求解 $[left,mid]$、$[mid+1,right]$。

求解每个被包含在当前区间中的询问区间 的答案的过程如下：

定义 DP 状态 fl[i][j] 表示在 $A_i\text~A_{mid}$ 中选出一些元素，这些元素之和模 $K$ 余 $j$ 的方案数；fr[i][j] 表示在 $A_{mid+1}\text~A_i$ 中选出一些元素，……（同上）的方案数。转移就没必要说了。先把这些 DP 值处理出来。

（感觉不是很方便叙述，不如我举个栗子）

  1. 询问区间跨过区间中点：

    jpg1

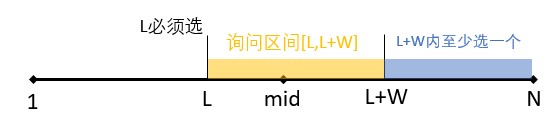
    那么询问区间的答案就是“必须选L，L+1~mid随便选的方案数”乘“mid+1~L+W-1随便选，L+W~right至少选一个的方案数”。用 DP 值表示就是 (fl[L][j]-fl[L+1][j])*(fr[right][j_]-fr[L+W-1][j_]) （其中 j 和 _j 之和为 K 或 0）。

  2. 询问区间完全在左区间：

    jpg2

    这样无法直接算出完整的答案，但是可以把答案拆成两步计算：
    ①必须选L，在 $[mid+1,right]$ 中至少选一个，$[L+1,mid]$ 随便选的方案数；
    ②必须选L，不在 $[mid+1,right]$ 中选，但是在 $[L+W,mid]$ 中至少选一个，$[L+1,L+W-1]$ 随便选的方案数；

    可以发现这两个方案加起来恰好能不重不漏地得到所有选择的方案。

    对于 ①，可以用当前的 DP 值计算出：(fl[L][j]-fl[L+1][j])*(fr[right][j_]-fr[mid][j_])；

    对于 ②，可以递归求解：在左区间 $[L,mid]$ 中求解，一定是能够计算完的。

算法思想就是这样。

复杂度分析其实很简单：因为这样取中点递归，最多会递归 $\log N$ 层；每一层计算 fl[i][j] 和 fr[i][j] 都需要枚举 i=1~N，j=0~K-1，均摊 $O(NK)$；枚举询问区间在每一层中也是 $O(N)$ 的。

因此复杂度是 $O(NK\log N)$。

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e5,MOD=1e9+7;
#define fix(x) (((x)%mod+mod)%mod)

int n,len,mod,cas;
long long ans;
int num[N+3],flef[N+3][50],frig[N+3][50];

void Solve(int lef,int rig){
	if(rig-lef<=len-1) return;
	if(rig==lef){
		if(num[lef]==0) ans=(ans+1)%MOD;
		return;
	}
	int mid=(lef+rig)>>1;
	Solve(lef,mid);Solve(mid+1,rig);
	for(int j=0;j<mod;j++) flef[mid+1][j]=frig[mid][j]=0;
	frig[mid][0]=1;flef[mid+1][0]
	for(int i=mid+1;i<=rig;i++)
		for(int j=0;j<mod;j++)
			frig[i][j]=(frig[i-1][j]+frig[i-1][fix(j-num[i])])%MOD;
	for(int i=mid;i>=lef;i--)
		for(int j=0;j<mod;j++)
			flef[i][j]=(flef[i+1][j]+flef[i+1][fix(j-num[i])])%MOD;
	for(int i=lef;i+len<=rig && i<=mid;i++)
		for(int j=0;j<mod;j++){
			int J=fix(mod-j);
			long long vlef=(flef[i][j]-flef[i+1][j]+MOD)%MOD,
					  vrig=(frig[rig][J]-frig[max(i+len-1,mid)][J]+MOD)%MOD;
			ans=(ans+vlef*vrig%MOD)%MOD;
		}
}
int main(){
	scanf("%d",&cas);
	while(cas--){
		scanf("%d%d%d",&n,&mod,&len);
		for(int i=1;i<=n;i++) scanf("%d",&num[i]);
		ans=0;
		Solve(1,n);
		printf("%lld\n",ans);
	}
	return 0;
}

The End

Thanks for reading!

啊，文化课要期末考试了!