学习笔记 - Z-Algorithm

又是一个非常冷门的算法 awa，换个名字可能会认得——扩展KMP

emm…… 然后在信息期末考试的时候，给材料现学现做了（然而那道题的难点并不是Z算法）

---

# 引入

感觉跟 KMP 关系不大，倒跟 Manachar 的思想比较接近。

在 Z算法 中，对于一个字符串 $S=\{S_0,S_1,\cdots,S_{n-1}\}$ 定义了一个函数 $Z(i)$，表示以位置 $i$ 开始的 $S$ 的后缀 $T_i=\{S_i,S_{i+1},\cdots,S_{n-1}\}$ 与 $S$ 的最长公共前缀的长度。
其中特殊定义 $Z(0)=0$。

暂且不管这个函数有什么用，先看看这个函数怎么算的。

---

# Z-Algorithm

我觉得 Z算法 的发明者应该是忽然想到 Z函数，然后感觉用 Z函数 可以搞大事情……
研究过后得到了这个算法

考虑从左到右依次计算 $Z(i)$。

> Tab.
以下区间 $[L,R]$ 均表示 $S$ 中从 $L$ 到 $R$ 的子串。注意 $S$ 下标从 $0$ 开始！

定义“匹配段”表示 目前已经计算得到的、是 $S$ 的前缀的子串，然后维护当前右端点最大的匹配段 $[L,R]$。

然后计算 $Z(i)$：

1. $i>R$：直接暴力枚举计算 $Z(i)$。

2. $i\le R$：
   因为 $[L,R]$ 是 $S$ 的前缀，也就是 $[L,R]=[0,R-L]$。那么一定有
   $[i,R]=[i-L,R-L]$，于是可以利用 已经计算出的 $Z(i-L)$ 计算 $Z(i)$。
   但是 $Z(i-L)$ 代表的子串并不一定等于 $[L,R]$，比如下面这样：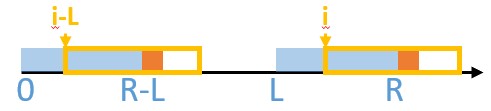
   

   也就是说：因为橙色位置可能不一样，所以 $Z(i)$ 不一定为 $Z(i-L)$。

   这时候就要缩小，缩成这样就没问题了：
   
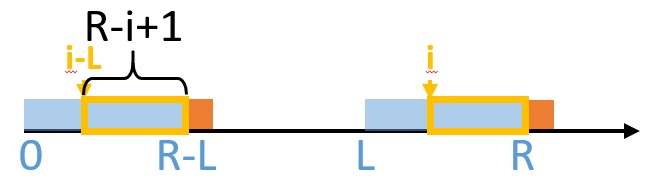
   也就是说，我们可以确定 $Z(i)$ 至少为 $\min\{Z(i-L),R-i+1\}$（跟Manachar那种计算方式特别像）
   然后 $Z(i)$ 可能还可以增大，于是继续暴力扩增 $Z(i)$。

---

# 代码实现

void ZAlgorithm(){
    //str 的下标从 0 到 n-1
    Z[0]=0;
    int right=0,left=0;
    for(int i=1;i<n;i++){
        if(i<=rig) Z[i]=min(Z[i-left],right-i+1);
        while(i+Z[i]<n && str[Z[i]]==str[i+Z[i]]) Z[i]++;
        if(i+Z[i]>right) left=i,right=i+Z[i];
    }
}

---

# 时间复杂度

与 Manachar 非常类似，看起来很暴力，实际上是 $O(n)$ 的复杂度（$n$ 是字符串长度）。

其实影响复杂度的只是 while 循环。

1. 如果 $Z(i)=Z(i-L)$，那么一定不会进入 while 循环，因为下一个位置已经不匹配了；
2. 如果 $Z(i)=right-i+1$，那么会造成 right 指针的右移。设右移的次数是 $t$，那么这样移动的复杂度是 $O(t)$ 的；
3. 如果 $i>right$，那么可以把过程看成：先把 right 指针指向 i（$O(1)$），然后归类到 2.。

于是 while 循环的均摊复杂度是 $O(\sum t)$，而 $\sum t\le n$，于是均摊复杂度是 $O(n)$。

如果只有 2. 情况，right 就会从 0 挪到 n，那么 $\sum t= n$；但是有 3. 情况，right 会直接跳到 i 位置，然后就会有 $\sum t<n$。

合起来就是 $\sum t\le n$。

---

The End

Thanks for reading!

信息期末考试有点放水……