理性愉悦(×)在线自闭(√)(和析合树有得一拼)
要感谢大神的博客:Meowww~(本文的证明思路同上博客)
# 概念
支配树是建立在单源有向图上的有根树。单源有向图又被称为“流程图”,其特点除了有向,还有存在一个源点使得源点可以到达任意一个点。
在流程图上定义支配关系,设源点为 $r$:如果 $r$ 到 $v$ 的每一条路径都经过了 $u$,则 $u$ 支配 $v$。
非常显然的,对于 $v$($v\neq r$) 来说,有两个平凡的支配点 $v,r$,一般来说都不会考虑 $v$ 本身作为 $v$ 的支配点。但是我们知道,往往是其他不平凡的支配点比较重要。
定义1-最近支配点
对于一个点 $v$($v\neq r$),如果 $u$ 是 $v$ 的一个支配点,并且任意一个 $v$ 的支配点都支配 $u$,则称 $u$ 为 $v$ 的最近支配点;记作 $\operatorname{idom}(v)=u$。
定理一
对于点 $v$,存在唯一的 $\operatorname{idom}(v)$。
首先支配关系具有一定的“传递性”,即如果 $a$ 支配 $b$、$b$ 支配 $c$ 则 $a$ 支配 $c$。则可以证明:
推论1
如果 $a$ 支配 $c$、$b$ 支配 $c$,则 $a$ 支配 $b$ 或 $b$ 支配 $a$。否则存在 $r$ 经过 $b$ 到达 $v$ 的路径不经过 $a$,与 $a$ 支配 $c$ 矛盾。
那么有且仅有一个 $v$ 的支配点支配 $v$ 的所有支配点,即 $\operatorname{idom}(v)$。
那么将 $\operatorname{idom}(v)$ 作为 $v$ 的父亲,可以获得一棵有根树,称为支配树。
接下来会介绍 Lengauer-Tarjan 算法,在 $O(n\log n)$ 时间复杂度内求出支配树,进而获得支配关系。
# 一些记号
先从流程图的源点出发DFS整张流程图,得到DFS树以及对应的DFS序。DFS树上有 4 种边:树边,前向边,后向边和横插边
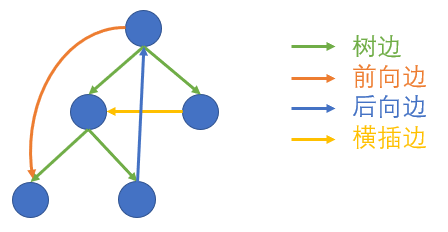
注意到横插边只会从右边的子树指向左边的子树,因此前向边和树边都是从低DFS序指向高DFS序,后向边和横插边就反过来。
- $u\to v$,表示 $u$ 到 $v$ 的一条有向边;
- $u\leadsto v$,表示存在 $u$ 到 $v$ 的一条路径;
- $u\overset .\to v$ 表示 $u$ 到 $v$ 的一条只经过树边的路径;
- $u\overset+\to v$ 表示 $u\overset.\to v$ 且 $u\neq v$;
- $dfn_u$ 表示 $u$ 的 DFS 序;
- 以下所有「点的大小比较」都是指 DFS 序进行比较。
# 理论证明
引理一(路径引理)
若 $dfn_u\le dfn_v$ 则 $u$ 到 $v$ 的路径必经过 $u,v$ 的公共祖先。
要么 $v$ 是 $u$ 的后继,要么 $v$ 是 $u$ 的更右边的子树中的点。
- 对于第一种情况,$u$ 就是公共祖先,必须经过;
- 对于第二种情况,考虑删去 $u,v$ 的 LCA 到 $r$ 的所有点(也就是删去所有公共祖先),此时不可能通过树边从 $u$ 的子树到达 $v$ 的子树;
另外前向边、后向边都不跨子树,而横插边只从右边的子树指向左边的子树,于是不存在向右跨越子树的边,不可能到达。
由于并不好计算 $\operatorname{idom}(u)$,所以考虑引入一些定义来辅助计算——
定义2-半支配点
点 $v$ 满足:存在路径 $P=v\leadsto u$,且 $P$ 上除去 $u,v$ 两点不存在 dfn 比 $u$ 小的点。
满足上述条件的最小的点 $v$ 称为 $u$ 的半支配点,记作 $\operatorname{sdom}(u)$。
形式化的定义为:
$$ \operatorname{sdom}(u)=\min\left\{v|\ \exists v\leadsto u=(v,a_1,a_2,\dots,a_m,u),a_i< u\right\} $$注意到 $\operatorname{sdom}(u)$ 并不一定是 $u$ 的一个支配点,比如下图:
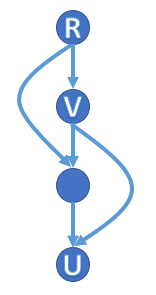
$v$ 是 $u$ 的半支配点但是显然不支配 $u$。
但是 $\operatorname{sdom}(u)$ 是有潜力成为支配点的点,在之后的证明中我们会看到任何一个点的 $\operatorname{idom}(u)$ 要么是 $\operatorname{sdom}(u)$,要么是另一个点的 $\operatorname{sdom}(v)$。
而且我们发现 $\operatorname{sdom}(u)\lt u$($u\neq r$),因为 $fa(u)$ 一定是 $u$ 的半支配点的「候选」。
引理二
对于任意 $u\neq r$,有 $\operatorname{idom}(u)\overset+\to u$ 且 $\operatorname{sdom}(u)\overset+\to u$。
如果 $\operatorname{idom}(u)$ 不是 $u$ 的祖先,那么 $r$ 就可以直接经过树边到达 $u$,就与 $\operatorname{idom}(u)$ 支配 $u$ 矛盾。
如果 $\operatorname{sdom}(u)$ 不是 $u$ 的祖先:
- 首先,$\operatorname{sdom}(u)$ 不可能是右边的子树或者 $u$ 的后继,因为 $\operatorname{sdom}(u)<u$,那么只能是左边的子树;
- 根据路径引理,从 dfn 小的点到大的点必然经过公共祖先,而 $u$ 和 $\operatorname{sdom}(u)$ 的公共祖先一定比 $u$ 小,违背了 $\operatorname{sdom}(u)$ 的定义。
引理三
对于任意 $u\neq r$,有 $\operatorname{idom}(u)\overset.\to \operatorname{sdom}(u)$。
考虑反证。根据引理二,$\operatorname{sdom}(u)$ 和 $\operatorname{idom}(u)$ 都是 $u$ 的祖先。所以如果引理三不成立,则 $\operatorname{sdom}(u)\overset+\to \operatorname{idom}(u)$。
因为 $\operatorname{sdom}(u)$ 可以不经过比 $u$ 小的点到达 $u$,即可以不经过 $\operatorname{idom}(u)$,则存在 $r\overset.\to \operatorname{sdom}(u)\leadsto u$ 不经过 $\operatorname{idom}(u)$,矛盾。
引理四
对于点 $w$,任意 $v\overset.\to w$ 满足 $v\overset.\to \operatorname{idom}(w)$ 或 $\operatorname{idom}(w)\overset.\to \operatorname{idom}(v)$。
由引理二,可以推得 $\operatorname{idom}(w),\operatorname{idom}(v),w,v$ 是在 $r\overset{.}{\to}w$ 上的。
仍然考虑反证。此时相反情况只有 $\operatorname{idom(v)}\overset{+}{\to}\operatorname{idom}(w)\overset{.}{\to}v\overset{.}{\to}w$,比如下面这样:
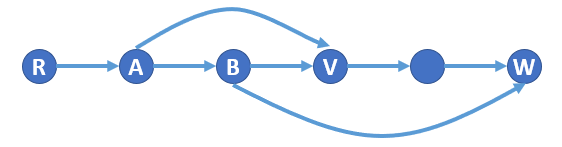
其中 $A,B$ 分别为 $\operatorname{idom}(v),\operatorname{idom}(w)$,注意到 $\operatorname{idom}(v)\neq\operatorname{idom}(w)$,故必然存在 $\operatorname{idom}(v)\leadsto v$ 不经过 $\operatorname{idom}(w)$。于是存在路径 $r\overset{.}{\to}\operatorname{idom}(v)\leadsto v\overset{.}{\to}w$,不经过 $\operatorname{idom}(w)$,矛盾。
完备的引理是对定理的铺垫~
定理二
对于 $u\neq r$,若所有满足 $\operatorname{sdom}(u)\overset+\to v\overset.\to u$ 的点 $v$ 都满足 $\operatorname{sdom}(v)\ge \operatorname{sdom}(u)$,则 $\operatorname{idom}(u)=\operatorname{sdom}(u)$。
这个定理就让 $\operatorname{idom}(u)$ 和 $\operatorname{sdom}(u)$ 有联系了~
由引理三,我们知道 $\operatorname{idom}(u)\overset.\to \operatorname{sdom}(u)$,则只需证明 $\operatorname{sdom}(u)$ 支配 u。考虑反证,假设 $\operatorname{sdom}(u)$ 不支配 u,则存在 $r\leadsto u$ 不经过 $\operatorname{sdom}(u)$。
记该路径为 $P=r\leadsto u$。令 $x$ 为 $P$ 上最后一个 $x\lt\operatorname{sdom}(u)$ 的点。
则 $x\leadsto u$ 上一定存在点 $y_0$ 满足 $\operatorname{sdom}(u)\overset.\to y_0\overset+\to u$($y_0$ 在 $\operatorname{sdom}(u)$ 和 $u$ 之间的链上),否则 $x$ 就会成为 $\operatorname{sdom}(u)$。记所有满足条件的点 $y_0$ 中最小的一个为 $y$。
若 $y\neq \operatorname{sdom}(u)$,由定理二得:$\operatorname{sdom}(y)\ge \operatorname{sdom}(u)$。
说明 $P$ 上还有一个点 $z$ 满足 $z\lt y$,否则 $x$ 将成为 $\operatorname{sdom}(y)$。那么有 $z\lt y\lt u$,但是 $y$ 是 $P$ 上最小的 $y\lt u$ 的点,产生矛盾。
则 $y=\operatorname{sdom}(u)$,因此 $P$ 一定经过 $\operatorname{sdom}(u)$,即 $\operatorname{sdom}(u)$ 支配 $u$。
定理三
对于 $w\neq r$,若存在 $u_0$ 满足 $\operatorname{sdom}(w)\overset+\to u_0\overset+\to w$ 使得 $\operatorname{sdom}(u_0)\lt\operatorname{sdom}(w)$;
记 $\operatorname{sdom}(u_0)$ 最小的 $u_0$ 为 $u$,则 $\operatorname{idom}(u)=\operatorname{idom}(w)$。
相当于是对定理二的补充。大概是这样一个图:

考虑 $\operatorname{idom}(u)$ 和 $\operatorname{idom}(w)$ 的位置。
- 首先 $\operatorname{idom}(w)\overset{.}{\to}\operatorname{sdom}(w)$ 且 $\operatorname{idom}(u)\overset{.}{\to}\operatorname{sdom}(u)$(引理三);
- 由引理四,因为 $u\overset{.}{\to}w$,且不存在 $u\overset{.}{\to}\operatorname{idom}(w)$,所以只能是 $\operatorname{idom}(w)\overset{.}{\to}\operatorname{idom}(u)$。
于是整个情形如下图:
只需要证明 $\operatorname{idom}(u)$ 支配 $w$。考虑证明非平凡情况:$\operatorname{idom}(u)\neq r$。
任意取一条路径 $P=r\leadsto w$,令 $P$ 中最后一个小于 $\operatorname{idom}(u)$ 的点为 $x$。则存在 $y_0$ 使得 $\operatorname{idom}(u)\overset.\to y_0\overset+\to w$,我们取最小的 $y_0$ 作为 $y$。
因为 $y$ 是满足条件的最小点,所以不存在 $v$ 使得 $\operatorname{idom}(u)\overset.\to v\overset+\to y$。于是 $x$ 是 $\operatorname{sdom}(y)$ 的「候选」,$\operatorname{sdom}(y)\le x\lt\operatorname{idom}(u)\le\operatorname{sdom}(w)$。
若 $\operatorname{sdom}(w)\overset{+}{\to}y\overset{+}{\to}w$,则 $y$ 可以作为定理中的 $u_0$,而 $\operatorname{sdom}(y)\le x\lt\operatorname{sdom}(u)$,与 $u$ 是 $\operatorname{sdom}(u_0)$ 最小的 $u_0$ 矛盾。
因此 $\operatorname{idom}(u)\overset{.}{\to}y\overset{.}{\to}\operatorname{sdom}(w)$。
此时,如果 $y\neq\operatorname{idom}(u)$,则存在 $r\overset{.}{\to}x\leadsto y\overset{.}{\to}u$ 不经过 $\operatorname{idom}(u)$,矛盾。故 $y=\operatorname{idom}(u)$。
因此任意路径 $P$ 都经过 $\operatorname{idom}(u)$,即 $\operatorname{idom}(u)$ 支配 $w$。
得证,$\operatorname{idom}(u)=\operatorname{idom}(w)$。
推论2
对于 $w\neq r$,令 $u$ 为 $\operatorname{sdom}(w)\overset+\to u\overset.\to w$ 中 $\operatorname{sdom}(u)$ 最小的,则有:
$$ \operatorname{idom}(w)=\begin{cases}\operatorname{sdom}(w)&\operatorname{sdom}(u)\ge \operatorname{sdom}(w)\\\operatorname{idom}(u)&\operatorname{sdom}(u)< \operatorname{sdom}(w)\end{cases} $$其实就是定理二三的综合。
最后只剩下如何求 $\operatorname{sdom}(w)$。
定理四
对于 $w\neq r$,$\operatorname{sdom}(w)$ 只可能是下面两种情况
- 存在边 $v\to w$,$\operatorname{sdom}(w)=v$;
- 点 $u$ 满足 $u\overset{.}{\to}v\to w$,其中 $v\gt w$,$\operatorname{sdom}(w)=\operatorname{sdom}(u)$。
形式化地:
$$ \operatorname{sdom}(w)=\min\{\{v|(v,w)\in E\}\cup\{\operatorname{sdom}(u)|u>w,\exists(v,w)\in E,u\overset.\to v\}\} $$显然两种情况都满足了 $\operatorname{sdom}(w)$ 的定义,只要证明 $\operatorname{sdom}(w)$ 一定符合两种情况之一:
- $\operatorname{sdom}(w)\leadsto w$ 只有一条边,对应第一个种情况;
$\operatorname{sdom}(w)\leadsto w$ 大于一条边,对应第二种情况,记第二种情况中 $\operatorname{sdom}(u)$ 的最小值为 $k$;则 $\operatorname{sdom}(w)\le k$。
记 $P=\operatorname{sdom}(w)\leadsto w$ 上 $\operatorname{sdom}(w)$ 以外的最小的点为 $y$。那么 $\operatorname{sdom}(w)\leadsto y$ 上除去 $\operatorname{sdom}(w), y$ 的所有点都大于 $y$,也即 $\operatorname{sdom}(w)$ 是 $\operatorname{sdom}(y)$ 的「候选」。
根据描述,$y$ 符合第二种情况中 $u$ 的定义,则 $k\le\operatorname{sdom}(y)$。
而 $\operatorname{sdom}(y)\le\operatorname{sdom}(w)$,所以 $k\le\operatorname{sdom}(w)$。
综上 $\operatorname{sdom}(w)=k$。
得证。
# Lengauer-Tarjan
有了上述定理作为基础,Lengauer-Tarjan算法就被设计出来,以 $O(n\log n)$ 的复杂度计算 $\operatorname{idom}(u),\operatorname{sdom}(u)$。
算法流程大概如下:
- 先DFS一遍,求一个DFS树,然后初始化 $\operatorname{sdom}(u)=u$(为了方便……);
- 根据定理四,按dfn从大到小枚举 $w$,计算 $\operatorname{sdom}(w)$(在每次计算前,$\gt w$ 的 $\operatorname{sdom}()$ 已经计算好了):
枚举连向 $w$ 的点 $u$,计算 $u$ 沿着 $fa(u)$ 往上爬到第一个dfn小于 $w$ 的点,这条路径上最小的 $\operatorname{sdom}()$。
当然我们不会直接枚举 $fa(u)$ 向上跳,需要用带权并查集维护有根树结构——每次计算完 $\operatorname{sdom}(w)$,就把 $w$ 在并查集中连向 $fa(w)$,并查集用路径压缩,压缩时更新路径上最小的 $\operatorname{sdom}(u)$ 对应的 $u$(详见代码)。 - 当我们计算完 $\operatorname{sdom}(w)$ 时,在并查集上 $w$ 的子树上所有点一定都连向了 $fa(w)$,因此可以枚举 $\operatorname{sdom}(u)$ 为 $fa(w)$ 的点 $u$,根据推论2,用带权并查集求出 $u$ 到 $\operatorname{sdom}(u)$ 的路径上最小的 $\operatorname{sdom}(v)$ 对应的 $v$,若 $\operatorname{sdom}(v)<\operatorname{sdom}(u)$,则给 $\operatorname{idom}(u)$ 打上“$v$ 的标记”,表示 $\operatorname{idom}(u)=\operatorname{idom}(v)$,否则直接 $\operatorname{idom}(u)=\operatorname{sdom}(u)$。
- 最后再扫一遍 $\operatorname{idom}(u)$,把有标记 $v$ 的 $\operatorname{idom}(u)$ 的值赋值为 $\operatorname{idom}(v)$。
Hint. 因为我们时常要取一个点的dfn做大小比较,写代码的时候注意变量到底代表的是dfn还是一个点本身。
# 源代码
> 洛谷 P5180
对应题目P5180【模板】支配树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96/*Lucky_Glass*/
using namespace std;
const int N=2e5+10,M=3e5+10;
struct LISTBLOCK{
int head[N],to[M],nxt[M],ncnt;
void Push(int u,int v){ncnt++;to[ncnt]=v,nxt[ncnt]=head[u],head[u]=ncnt;}
int operator [](const int &u){return head[u];}
void Init(int siz){for(int i=0;i<=siz;i++) head[i]=0;ncnt=0;}
void Clear(int id){head[id]=0;}
}In,Out,Bucket;
int n,m,ndfn;
int idfn[N],dfn[N],pre[N];
int idom[N],sdom[N];
int ans[N];
void CalcAns(int u){
ans[u]=1;
for(int it=Out[u];it;it=Out.nxt[it]){
int v=Out.to[it];
CalcAns(v);
ans[u]+=ans[v];
}
}
struct DSU{
int fa[N],val[N];
int Find(int u){
if(u==fa[u]) return u;
int res=Find(fa[u]);
if(sdom[val[fa[u]]]<sdom[val[u]]) val[u]=val[fa[u]];
return fa[u]=res;
}
int Eval(int u){Find(u);return val[u];}
bool Link(int u,int v){
u=Find(u),v=Find(v);
if(u==v) return false;
fa[u]=v;
return true;
}
void Init(int siz){for(int i=0;i<=siz;i++)fa[i]=i,val[i]=i;}
}Ds;
inline int Ri(){
register int a=0,c=getchar();
while(c<'0' || '9'<c) c=getchar();
while('0'<=c && c<='9') a=(a<<1)+(a<<3)+c-'0',c=getchar();
return a;
}
void DFS(int u){
idfn[sdom[u]=dfn[u]=++ndfn]=u;
for(int it=Out[u];it;it=Out.nxt[it]){
int v=Out.to[it];
if(dfn[v]) continue;
pre[v]=u,DFS(v);
}
}
int main(){
n=Ri(),m=Ri();
for(int i=1;i<=m;i++){
int u=Ri(),v=Ri();
In.Push(v,u),Out.Push(u,v);
}
DFS(1);
Ds.Init(n);
for(int i=ndfn;i>=2;i--){
int u=idfn[i];
for(int it=In[u],v=In.to[it];it;it=In.nxt[it],v=In.to[it])
if(dfn[v])
sdom[u]=min(sdom[u],sdom[Ds.Eval(v)]);
Bucket.Push(idfn[sdom[u]],u);
// printf("! %d %d\n",u,idfn[sdom[u]]);
Ds.Link(u,pre[u]);
int pu=pre[u];
// printf("? %d\n",pu);
for(int it=Bucket[pu];it;it=Bucket.nxt[it]){
int iv=Bucket.to[it],iu=Ds.Eval(iv);
idom[iv]=sdom[iu]==sdom[iv]? pu:iu;
}
Bucket.Clear(pu);
}
for(int i=2,u=idfn[i];i<=ndfn;i++,u=idfn[i])
idom[u]=idfn[sdom[u]]==idom[u]? idom[u]:idom[idom[u]];
for(int i=2,u=idfn[i];i<=ndfn;i++,u=idfn[i])
sdom[u]=idfn[sdom[u]];
Out.Init(n);
for(int i=2;i<=n;i++) Out.Push(idom[i],i);
CalcAns(1);
for(int i=1;i<=n;i++)
printf("%d%c",ans[i],i==n?'\n':' ');
return 0;
}
THE END
Thanks for reading!
只要极致 谁比我放肆
展开双翅 去奔跑 像个孩子
写下你的名字 在风中化成诗
再说一次 不在乎方式
哪怕重新开始 那也要坚持
别去拔你的刺 那是你最美丽的旗帜
——《奔赴》By 司南
> Linked 奔赴-网易云