前行 - 非集训队作业Ⅰ | Lucky

然而并不是集训队作业 ←.←
#更新结束# 下一章：非集训队作业Ⅱ

# 小引

今年的OI被疫情~~和CCF与教育部的明争暗斗~~搞得乱七八糟的，终于要迎来最后一轮比赛了，希望能够有一个更好的结果。（立🚩）

连省队都没进就别说集训队了 awa 不过要想提高的话不刷些自闭题是不可能的 (╹ڡ╹ )

# T1 - Distance Sums (Atcoder)

> Linked AtCoder ARC103-F

点击展开/折叠题面

给出 $n$ （$1\le n\le10^5$）和 $a_1,a_2,\dots,a_n$，$a_i$ 互不相同，构造一棵 $n$ 个点的有标号树，使得点 $i$ 与其他所有点的距离之和为 $a_i$。

一条条加边，则最初图中没有边，每个点都是一个 siz 为 $1$ 的点（因为之后的过程涉及缩点，一个“点”的 siz 会改变）。则有结论——如果以重心为根，$a_i$ 最大的点一定是一个“叶子节点”。

考虑从一个点 $u$ 的 $a_u$ 与其相邻点 $v$ 的 $a_v$，设断掉边 $(u,v)$ 后 $u,v$ 所在连通块大小分别为 $S_u,S_v$，则 $a_u-a_v=S_v-S_u$。那么对于所有不是根的节点 $u$ 一定有 $siz_u<\tfrac n2$，设其父亲为 $v$，则 $S_u-S_v=(n-siz_u)-siz_u>0$，也就是说从根到叶子的路径上 a 值递增。

于是直接取 $a_u$ 最大的点 $u$ 作为叶子，然后其父亲的 a 值是 $a_u-n+2siz_u$，由于 $a_i$ 互不相同，如果找到了满足条件的点 $v$，则 $v$ 就是 $u$ 的父亲，否则无解。

这样可以构造出来一棵树，于是我们就可以WA掉3个点了……因为我们只判断了点 $u$ 和它父亲的 a 值之差是否满足条件，但是没有验证根的 a 值是否满足条件，加一次验证即可。

# T2 - RNG and XOR

> Linked AtCoder AGC034-F

点击展开/折叠题面

给定整数 $n$（$n\le18$）和 $a_0,a_1,\dots,a_{2^n-1}$，设所有 $a_i$ 之和为 $S$。有一个变量 $x$ 初始值为 $0$，进行若干次操作：以 $\tfrac {a_i}S$ 的概率选择数 $i$，将 $x$ 异或 $i$。对于所有 $k\in[0,2^n-1]$，求期望进行多少次操作使得 $x$ 第一次变成 $k$。

由于是“第一次达到”这样的期望问题，就必须设置一个明确的终止状态。如果正向考虑，则要求第一次达到 $k$ 的期望就需要设置 $x=k$ 的剩余期望次数为 $0$，这样每次的终止状态都不同，不好处理。但根据异或的可逆性，“从 $0$ 开始第一次异或出 $i$”相当于“从 $i$ 开始第一次异或出 $0$”，这样终止状态唯一。

常规定义 $f_i$ 表示 $x=i$ 时期望多少次可以第一次变为 $0$，则 $f_0=0$。对于 i>0 易得（$N=2^n$）：

$f_i=\tfrac1{S}\sum_{j=0}^{N-1}a_jf_{i\oplus j}+1$

看到一个非常异或卷积的式子，不妨向异或卷积靠：

$\begin{align} Sf_i-S=\sum_{j=0}^{N-1}a_jf_{i\oplus j} \end{align}$

根据 $FWT(A)_i=\sum(-1)^{\text{popcount}(i\&j)}a_j$ 可得

$FWT(kA+b)_i=\begin{cases}kFWT(A)_0+Nb&i=0\\kFWT(A)_i&i>0\end{cases}$

结合之前的式子似乎可以得到

$FWT(Sf_i-S)=FWT(A)\times FWT(F)$

但是我们发现 $f_0$ 并不满足式 (1)，所以上式不成立，为了能够利用上式，我们不妨设 $f’_i$ 对于 $i\in[1,N-1]$ 满足 $Sf_i’-S=\sum_{j=0}^{N-1}a_jf_{i\oplus j}$，则有：

$FWT(Sf'_i-S)=FWT(A)\times FWT(F)$

展开则有：

$\begin{aligned} &FWT(Sf'_i-S)_0=S\cdot FWT(F')_0-NS=FWT(A)_0\times FWT(F)_0\\ &FWT(Sf_i'-S)_k=S\cdot FWT(F')_k=FWT(A)_k\times FWT(F)_k \end{aligned}$

不难发现，$F’$ 和 $F$ 唯一的区别就是 $f’_0$ 和 $f_0$，根据 $FWT$ 的计算方式可得 $FWT(F’)_k-f’_0=FWT(F)_k$ 。则有：

$\begin{align} S\cdot FWT(F)_0-NS+f'S=FWT(A)_0\times FWT(F)_0\\ S\cdot FWT(F)_k+f'S=FWT(A)_k\times FWT(F)_k \end{align}$

根据 FWT 的计算方式，$FWT(A)_0=S$，则根据 (2) 式有：$f’=N$。根据 (3) 式有：

$FWT(F)_k=\frac{f'S}{FWT(A)_k-S}$

我们就可以求出 $FWT(F)$ 的 $[1,N-1]$ 项，只需再求出 $FWT(F)_0$ 就可以 IFWT 回去得到 $\{f_i\}$ 了，而根据 $FWT(F)$ 的性质，有：

$Nf_0=\sum_{i=0}^{N-1}FWT(F)_i$

则

$FWT(F)_0=-\sum_{i=1}^{N-1}FWT(F)_i$

最后 IFWT 回去就可以了。

# T3 - Stop. Otherwise…

> Linked AtCoder ARC102-E

点击展开/折叠题面

有 $n$ 个无区别的骰子（$n\le2000$），每个可以投出 $1\sim m$ 的点数。对于每个 $x=2\sim 2m$，求有多少种投出骰子的情况使得没有任何两个骰子的点数和为 $x$。

转换成每个点数的骰子有多少个，就直接分类讨论+生成函数……

如果 $t\le m$，则点数为 $t\sim m$ 的骰子数量无限制，而 $i$ 和 $t-i$ 要么两种点数都没有，要么其中一个有；
- 如果 $t$ 是奇数，则 $t\sim m$ 的生成函数可以是 $(1+x+x^2+\dots)^{m-t+1}$，而 $i$ 和 $t-i$ 就看成同一种点数，如果有该点数的骰子，则提供 $\times2$ 的贡献，否则提供 $\times1$ 的贡献，即 $(1+2x+2x^2+\dots)^{\lfloor t/2\rfloor}$；
- 如果 $t$ 是偶数，则 $t\sim m$ 的生成函数没变，对于 $i=t/2$ 这一种点数，最多只能有一个，则生成函数为 $(1+x)$，其余仍然把 $i$ 和 $t-i$ 看作一种点数，生成函数为 $(1+2x+2x^2+\dots)^{t/2-1}$；
如果 $t>m$，则无限制的点数是 $1\sim t-m-1$，其余同理；

最后推出来的生成函数就是：

$[x^n] \begin{cases} (1+x+x^2+\dots)^{m-t-1}(1+2x+2x^2+\dots)^{(t-1)/2}&2\not\mid t,t\le m\\ (1+x)(1+x+x^2+\dots)^{m-t-1}(1+2x+2x^2+\dots)^{t/2-1}&2\mid t,t\le m\\ (1+x+x^2+\dots)^{t-m-1}(1+2x+2x^2+\dots)^{(2m-t+1)/2}&2\not\mid t,t>m\\ (1+x)(1+x+x^2+\dots)^{m-t-1}(1+2x+2x^2+\dots)^{(2m-t-1)/2}&2\mid t,t>m \end{cases}$

至于 $(1+2x+2x^2+\dots)^k$ 怎么处理，就当成是 $\left(\frac{2}{1-x}-\frac12\right)^k$ 然后二项式展开即可。

# T4 - Gachapon

> Linked AtCoder AGC038-E

点击展开/折叠题面

有一个随机数生成器，生成 $[0,n-1]$ 的整数，生成 $i$ 的概率为 $\frac{a_i}{S}$，其中 $S=\sum a_i$。

生成器不断生成随机数，当 $\forall i$，$i$ 生成的次数至少有 $b_i$ 次时，停止生成。

求期望生成多少次随机数。

$\sum a_i,\sum b_i,n\le400$

一种我已经忘了的 min-max 反演方法……

$E\left(\max_{i\in U}\{t_i\}\right)=E\left(\sum_{S\subset U}(-1)^{|S|+1}\min_{i\in S}\{t_i\}\right)=\sum_{S\subset U}(-1)^{|S|+1}E(\min_{i\in S}\{t_i\})$

这道题的 $t_i$ 就是第 $i$ 个数出现恰好 $b_i$ 次的时间，而 $E(\min_{i\in S}\{t_i\})$ 就是 $S$ 中恰好有一个数生成了 $b_i$ 次的期望时间。

又根据套路：“结束状态的期望时间=所有未结束状态的概率之和”（实际上是概率 $\times1$，即每种状态提供 $1$ 的时间贡献，由期望的线性性可以求和）。

$E\left(\min_{i\in S}\{t_i\}\right)=\sum_{t}[\forall{i\in S},t_i<b_i]P(t)$

由于对于子集 $S$，我们只关心 $i\in S$ 的 $t_i$，所以状态 $w$ 中实际上是不包含 $S$ 以外的信息的，于是要把“一个确切的局面 $t$ ”转化成“一个状态 $w$”（状态包括多个局面）。定义一个状态 $w$ 持续的期望时间是 $e_w$，可以得到：

$\sum_{t}[\forall{i\in S},t_i<b_i]P(t)=\sum_{w}P(w)e_w$

当生成一个 $S$ 中的数字时，状态 $w$ 就会改变，设生成一个 $S$ 中的数字的概率是 $P_S$，由一个非常广为人知的结论可以得到状态 $w$ 的期望持续时间为 $\frac1{P_S}$。

而

$\begin{aligned} C(w)&=\sum_{i\in S}a_i,X(w)=\sum_{i\in S}b_i\\ P(w)&=X(w)!\prod_{i\in S}\left(\frac {a_i}{C(w)}\right)^{w_i}\frac{1}{w_i!}=\frac{X(w)!}{C^{X(w)}(w)}\prod_{i\in S}\frac{a_i^{w_i}}{w_i!} \end{aligned}$

设计DP：$f_{C,X}$ 表示 $C(w)=C,X(w)=X$ 的 $\prod_{i\in S}\frac{a_i^{w_i}}{w_i!}$ 带上容斥系数的和。转移决策 $i=0\sim n-1$ 是否加入已有的状态里（$i$ 是否加入集合 $S$），以及加入多少次（$w_i$），类似于一个背包。复杂度 $O((\sum b_i)^2\sum a_i)$ 。

# T5 - Manju Game

> Linked AtCoder AGC026-F

点击展开/折叠题面

有 $n$ 个数字（$n\le3\times 10^5$），A,B进行博弈。A 是先手，A,B轮流进行下面的操作：

如果当前是第一次选择数字，或对手上一次选择的数字的相邻两个数字都被选择了，则任意选择一个没有被选择的数字。
否则任意选择与对手上一次选择的数字相邻的、没有被选择的数字。

A,B都想要最大化自己选的数字之和，求最优策略下，A,B最后的数字和各自是多少。

我们发现操作大致可以理解为：“先手”随便取一个位置，“后手”决定一个方向，然后先后手轮流取，直到不能取（这样称作一个回合）。显然这样操作，每个回合后，可以取的数字是一个连续的区间。

那么先手在一个回合中的第一次操作可以分为两类：

直接取剩下的区间的端点，后手没有选择，该回合轮流取，博弈结束；
取中间的一个数，后手决定方向，回合结束后博弈继续。

我们发现在一个回合后，A,B 在下一回合的先后手关系可能改变，取决于该回合取的数量的奇偶性。先手取数 $i$ 后，会将剩余区间 $[l,r]$ 分成两半 $[l,i-1],[i+1,r]$，后手决定取哪一个区间，不妨对两个区间的奇偶性进行讨论：

如果两个区间中有至少一个的大小是偶数，则后手存在策略：取偶数长度的区间，比如 ---Oxoxo（- 表示未取，o 表示先手，O 是先手第一次取的位置，x 表示后手）

则下一回合先后手交换，后手可以有下面的取法 xoxOxoxo 使得局面与“先手直接取区间端点”的结果相同。意味着此时先手的决策不优于直接取端点。
如果两个区间的大小都是奇数，则先手要么取两端之一，结束博弈，要么取一个点，后手取一个方向，一个回合后先后手顺序不变；剩下一段区间继续博弈。

如果当前区间是偶数长度，显然先手无论怎么分，分出的区间都有偶数长度的，所以此时先手最优策略就是直接取端点。

如果当前区间是奇数长度：

先手若把它分为两个偶数长度的区间，则根据之前的结论，后手可以使其结果不优于先手直接取端点的结果。
否则后手选择一个方向，留下两个区间之一。

除非先手直接结束博弈（取区间端点），先手一定不会分出两个偶数长度的区间。于是最终局面会变成——先手取了 $[1,l-1]$ 中的偶数位置、$[l,r]$ 的奇数位置和 $[r+1,n]$ 的偶数位置（$l,r$ 都是奇数），其中 $[l,r]$ 就是最后一个回合操作的区间，先手直接取其端点使博弈结束。

不妨设先手只取了所有偶数位置，需要再选出一个区间 $[l,r]$ 并将里面的选择关系反转，使得 $[l,r]$ 中“奇数位置和-偶数位置和”最大。考虑二分“奇数位置和-偶数位置和”的大小，于是我们可以得到哪些区间满足条件（称这些区间为“合法区间”），设为 $[l_1,r_1],[l_2,r_2],\dots,[l_k,r_k]$，只要先手能让反转的区间是这些区间之一就可以满足二分的条件。

一个区间能否反转就是看它能否成为最后一个回合的区间（当然还得是一个奇数长度的区间）。于是我们得到结论——如果存在一系列 $[l_{p_i},r_{p_i}]$ （$i\in[1,t]$）使得 $r_{p_{i-1}}+1=l_{p_{i}}-1$，且 $l_{p_1}=1,r_{p_t}=n$，则可以满足条件，如下图：

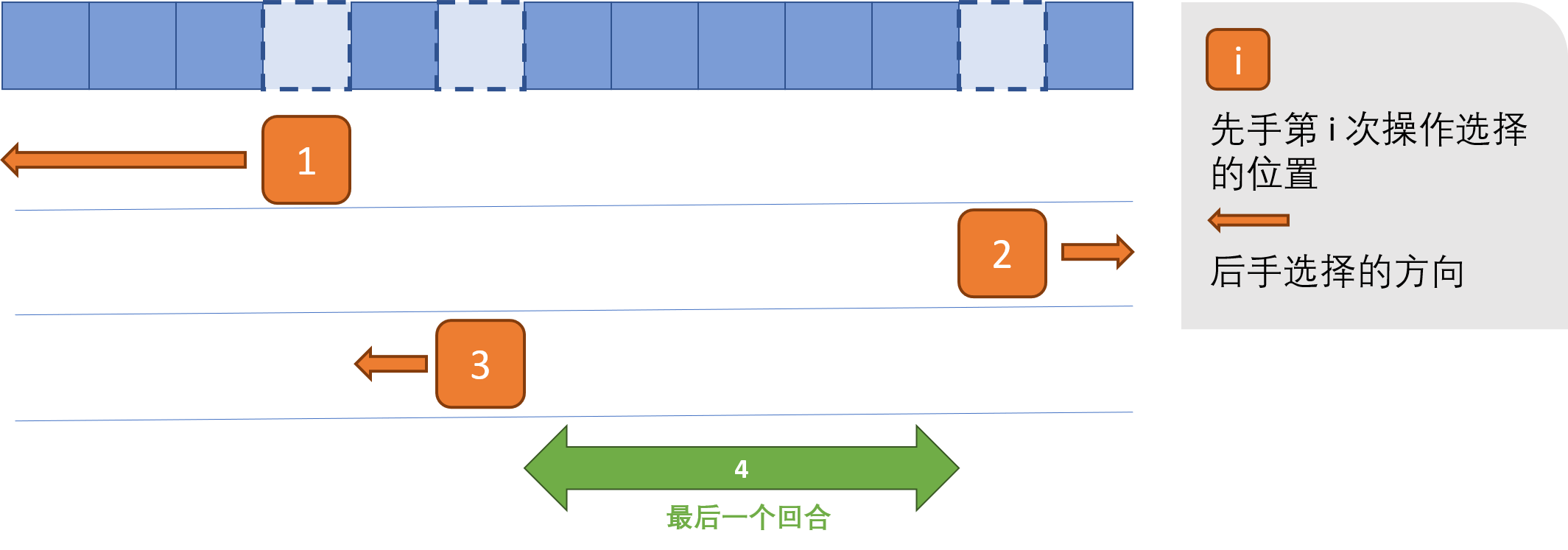
反之，如果不能这样“首尾相接”，后手就一定可以将剩余区间引导到一个不能被划分成若干合法区间的方向，则不满足条件。

于是做一个简单的 dp，设 $f_i$ 表示前 $i$ 个位置能否被划分为合法区间，可以优化到 $O(1)$ 转移。因此 DP 复杂度 $O(n)$，总复杂度 $O(n\log n)$。

# T6 - Donation

> Linked AtCoder ARC098-F

点击展开/折叠题面

$n$ 个点，有 $m$ 条无向边使它们构成一个连通图（$1\le n,m\le10^5$）。每个点有两个参数 $A_i,B_i$，表示你从另一个点到达该点时（或者你从该点出发时）至少要有 $A_i$ 元钱，你在该点时，可以选择给该点贡献 $B_i$ 元钱，但是结束时，你必须给每个点恰好贡献一次。你可以随便选择一个点开始，求你开始时最少需要带多少钱。

有个比较显然的性质是在最优策略下，一定是在最后一次到达这个点时进行贡献。如果不是，我们可以把贡献改到最后一次到达该点时进行贡献，显然仍然满足要求。

然后有一个重要的转化——“到达点 $u$ 时至少有 $a_u$ 元钱” 等价于 “离开点 $u$ 时至少有 $a_u-b_u$ 元钱”，即考虑最后一次到达该点，首先必须有 $a_u$ 元钱，然后贡献 $b_u$ 元钱后离开，之后就不再到达点 $u$。

令 $c_u=a_u-b_u$，则贪心地想，先去 $c_u$ 大的点进行贡献，之后就不经过 $u$ 了。

于是先取出 $c_u$ 最大的 $u$，把这个点删去得到若干个连通块，设为 $G_1,G_2,\dots,G_k$；则根据之前的结论，我们要先把 $G_{1\sim i-1},G_{i+1\sim k}$ 全部贡献完，然后贡献 $u$，再走到 $G_i$ 里面就不返回 $u$ 了。

可以看出上述递归处理问题的方式形成了一个树形结构——当前的 $c_u$ 最大点 $u$ 作为当前连通块的“根”，把连通块分成若干连通分量，而连通分量里的 $c_v$ 最大点 $v$ 又作为连通分量的“根”，$(u,v)$ 表现为父子关系。这样的树形结构中，父亲的 $c$ 大于等于儿子。

于是考虑树形DP——$f_u$ 表示把子树 $u$ 所代表的连通块全部贡献完最少需要带多少钱。设 $tot(u)$ 表示 $u$ 子树内的 $b$ 之和。则：

$\begin{align} &f_u:=tot(u)+c_u\\ &f_u:=\min_v\{f_u,tot_u-tot_v+\max\{f_v,c_u\}\} \end{align}$

(4) 即表示把子树 $u$ 贡献完后又返回 $u$，除去需要贡献的 $tot(u)$ 元钱，离开 $u$ 时至少还有 $c_u$ 元。因为 $u$ 是当前连通块的 $c$ 最大点，只要贡献后剩的钱足够 $c_u$，也一定满足其他点的限制。

(5) 即表示先进入其他连通分量完成贡献，再贡献 $u$，最后进入连通分量 $G_v$ 贡献。在其他连通分量和 $u$ 中总共贡献 $tot(u)-tot(v)$，离开 $u$ 进入 $G_v$ 时，至少要有 $c_u$ 元，在 $G_v$ 最少需要带 $f_v$ 元，所以是 $\max\{f_v,c_u\}$。

# T7 - Simple Subsequence Problem

> Linked AtCoder AGC024-F

点击展开/折叠题面

给定一个01字符串集合 $\mathbb S$，求在长度最长的前提下，字典序最小的字符串 $c$，使得 $c$ 是 $\mathbb S$ 中的至少 $k$ 个串的子序列。

$\mathbb S$ 中串的长度 $\le20$

只要对任意一个串 $c$，求出它是 $S$ 中多少个串的子序列，就可以迅速找到答案了。

先不考虑怎么求它的出现次数，我们先看如何判断 $c$ 是否是一个串 $T$ 的子序列。非常简单，只需要贪心地找到 $T$ 中第一个 $c_0$ 并匹配即可，然后转移到下一次匹配。

于是类似于 DP 把状态存下来的方法（个人觉得尤其像动态DP把内层DP状态存下来），我们储存这样的状态：$f(S,T)$ 表示已经匹配出子序列 $S$，原串剩下的串为 $T$，在 $\mathbb S$ 中满足多少个串。可见 $S,T$ 的长度之和不超过 $20$，则状态数相当于把一个长度不超过 $20$ 的01串分成前后两个部分的方案数，不超过 $2^{21}*21$。

则初始值有 $f(\varnothing,c)=1$（$c\in\mathbb S$），而转移，设 $next_0(S),next_1(S)$ 分别表示在 $S$ 中匹配第一个 $0$ 或 $1$ 后剩下的串：

$f(S,T)\to f(S+0,next_0(T))\\ f(S,T)\to f(S+1,next_1(T))\\ f(S,T)\to f(S,\varnothing)$

注意第三个转移，因为子序列的匹配可以在任意时刻结束。

$next$ 函数可以一开始 $O(2^nn)$ 处理，而 DP 是没有环的，可以一次 $O(2^nn)$ 拓扑转移。但是注意常数……状态储存尽量优美，比如我的储存方法是：

f[i][j] 其中 i 是字符串 1+S+T，要在 S 前加 1 是标记 S 的开头位置，因为 S 有前导零，j 是标记 T 的长度，这样设计状态的好处在于，转移 f[i][j] -> f[p][q] 都有 $i>p$ 或 $i=p,j> q$。

THE END

Thanks for reading!

$\begin{split} “\ &我看不到你内心真实的想法\\ &也不奢望感同身受成为依靠臂膀\\ &也许我们注视着同样的地方\\ &聚着光\ 被照亮\ ”\\ ——&\text{《你别忘》By 泠鸢yousa} \end{split}$

> Linked 你别忘-网易云