学习笔记 - 可持久化线段树 | Lucky_Glass's Blog

以心为名，名为爱惜

0%

学习笔记 - 可持久化线段树

发表于 更新于 分类于 Valine：

就像十二省联考 的出题人所说 “无论省选对于你意味着什么，都希望你能拥有光明的未来”

所以我就开始学可持久化的一系列数据结构了……从不带修改的可持久化线段树学起~

· 引入

- 什么是可持久化？

一个具有可持久化性质的数据结构能够保存自己的历史版本；

也就是说它每一次修改不会修改原来的结构（旧版本），而是创建新的结构（新版本）。当然这样在内存、时间上都会有一个比较大的开销（对于时间往往是常数开销），所以我们对一些数据结构做可持久化时进行了一些优化。

- 线段树的可持久化

考虑最简单的实现可持久化的方法（当然这样内存开销会非常大）—— 每次修改时将旧版本整个 copy 到新版本上，再在新版本上做修改。

我们发现由于只修改一次，也就是新版本上只有从根出发的一条路径上的节点被修改了，而其他大多数节点都与就版本相同。于是可以想到这些节点可以沿用旧版本，而不新建节点。这就是可持久化线段树 实现的原理。

· 可持久化

- 前置

  1. 权值线段树：和普通线段树结构上相同，但是它的节点表示的是一个值域 $[l,r]​$，该节点的大小为 $a_i\in[l,r]​$ 的 $i​$ 的个数；
    通俗一点就是说对于某个节点，它的左右端点为 $l,r​$ ，那么它的值就是 大于等于 $l​$ 小于等于 $r​$ 的数的个数。

  2. 离散化；

- 可持久化的实现

简单的说就是 只有要修改的节点才新建，其余保留旧版本 。
举个例子来说明：建立一棵根节点为区间 $[1,4]$ 的权值线段树，最开始所有节点的大小都为 $0$：

img1

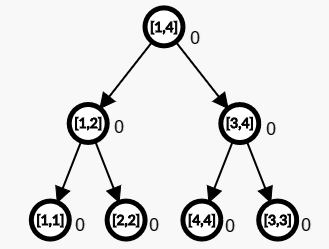
然后插入一个 $1$ ，步骤如下：

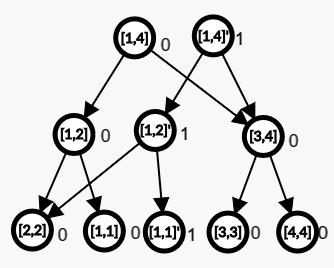
  1. 从根节点出发，由于 $1\in [1,4]$ ，所以根节点要修改，于是建立一个新版本的根节点；
  2. 发现 $1\in[1,2]$ ，但 $1\not\in[3,4]$ ，所以 创建新版本的节点$[1,2]$ ，节点$[3,4]$ 不新建；
  3. 从新版本的 节点$[1,2]$ 继续插入；
  4. 直到插入到叶子节点 $[1,1]$ ，插入完成。

最后就变成了下面这样：

img1

- C++实现

1
2
3
4
5
6
7
8
9
10
//rt是当前位置的新版本节点；prt是当前位置的旧版本节点
void Insert(NODE *&rt,NODE *prt,int val,int lef,int rig){ //NODE是节点的结构体，这里用的是指针线段树
	rt=++ncnt; //ncnt指向一个新的节点
	*rt=*prt; //新版本节点继承旧版本节点信息
	rt->siz++; //新版本中值+1
	if(lef==rig) return;
	int mid=(lef+rig)>>1;
	if(val<=mid) Insert(rt->ch[0],prt->ch[0],val,lef,mid); //插入到左子树，则新建左儿子节点
	else Insert(rt->ch[1],prt->ch[1],val,mid+1,rig); //插入到右子树，则新建右儿子节点
}

· 可持久化线段树的用途

比较常见的就是在 $O(\log n)​$ 内静态（无修改）查询一个数列中某一段数的第 $k​$ 大了。（##POJ - 2104##）

给出 $n​$ 个数 $a_1…a_n​$ 以及 $m​$ 个询问；
询问为：求 $a_l…a_r​$ 的第 $k​$ 大

我们可以把可持久化线段树的“第$k$个版本”看成只插入了 $a_1…a_k$ 的权值线段树。

定义两棵权值线段树“相减”为对应节点的权值相减。根据前缀和的思想，插入了 $a_l…a_r$ 的权值线段树就是 版本$r$ - 版本 $(l-1)$ 。

假设 版本$r$ 和 版本$(l-1)$ 的表示区间 $[Lef,Rig]$ 的节点分别为 rt,prt​ ，且已经确定“第$k$大”在 $[Lef,Rig]$ 中。定义 $Mid=\lfloor\frac{Lef+Rig}2\rfloor$ ，则 $[Lef,Mid]$ 的数量为 rt的左儿子大小 减去 prt 的左儿子大小，记这个数量为 totlef。如果 $k\leq totlef$ ，则说明 $[Lef,Rig]$的第$k$大 是 $[Lef,Mid]$的第$k$大；否则 $[Lef,Rig]$的第$k$大 是 $[Mid+1,Rig]$的第$(k-totlef)$大。

Tab. 需要离散化，而且记得把数组开大一点

· 源代码

（打了包，直接可以用，题目是 POJ-2104）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5;
struct SEGTREE{
	struct NODE{
		int siz;
		NODE *ch[2];
	};
	NODE nod[20*N],*root[N+3],*ncnt;
	void Rebuild(){memset(nod,0,sizeof nod);memset(root,0,sizeof root);ncnt=&nod[0];}
	void Build(NODE *&rt,int lef,int rig){ //建立版本0的空线段树
		rt=++ncnt;
		if(lef==rig) return;
		int mid=(lef+rig)>>1;
		Build(rt->ch[0],lef,mid);
		Build(rt->ch[1],mid+1,rig);
	}
	void Insert(NODE *&rt,NODE *prt,int val,int lef,int rig){ //插入值val
		rt=++ncnt;
		*rt=*prt;rt->siz++;
		if(lef==rig) return;
		int mid=(lef+rig)>>1;
		if(val<=mid) Insert(rt->ch[0],prt->ch[0],val,lef,mid);
		else Insert(rt->ch[1],prt->ch[1],val,mid+1,rig);
	}
	int Query(NODE *rt,NODE *prt,int rnk,int lef,int rig){ //查询[lef,rig]中的第rnk大
		if(lef==rig) return lef;
		int mid=(lef+rig)>>1;
		int lsiz=rt->ch[0]->siz-prt->ch[0]->siz;
		if(rnk<=lsiz) return Query(rt->ch[0],prt->ch[0],rnk,lef,mid); //答案在 左子树 里
		else return Query(rt->ch[1],prt->ch[1],rnk-lsiz,mid+1,rig); //答案在 右子树 里
	}
}segtre;
int n,m,fn;
int num[N+3],cpy[N+3];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&num[i]),
		cpy[i]=num[i];
	sort(cpy+1,cpy+1+n);
	fn=unique(cpy+1,cpy+n+1)-(cpy+1); //离散化，去重；fn是去重后数组的长度
	segtre.Rebuild();
	segtre.Build(segtre.root[0],1,fn);
	for(int i=1;i<=n;i++){
		int id=upper_bound(cpy+1,cpy+1+fn,num[i])-(cpy+1);
		segtre.Insert(segtre.root[i],segtre.root[i-1],id,1,fn);
	}
	for(int i=1;i<=m;i++){
		int lef,rig,rnk;
		scanf("%d%d%d",&lef,&rig,&rnk);
		printf("%d\n",cpy[segtre.Query(segtre.root[rig],segtre.root[lef-1],rnk,1,fn)]);
	}
	return 0;
}

The End

Thanks for reading!

Email: lucky_glass@foxmail.com ，欢迎提问~