学习笔记 - 凸优化 | Lucky_Glass's Blog

以心为名，名为爱惜

0%

学习笔记 - 凸优化

发表于 更新于 分类于 Valine：

果然 Tiw 讲的课都会自闭……

Part1. 凸优化

又称 带权二分,wqs分治。

“带权二分”表现了算法的实现，“凸优化”揭示了算法的本质，“wqs分治”表述了将其引入OI的人

- Tiw_Air_OAO

Part1/1. 适用范围

凸优化适用于一类限制了“恰好有 k 个……”的题目。

> 听起来是不是非常广泛？但它还有一个条件。

既然算法名字里面带 “凸” —— 凸包！定义 $f(t)$ 表示当 k=t 时，题目所求的最优答案。那么 $f(t)$ 必须满足一个凸性质，即 $(t,f(t))$ 要么形成上凸包，要么形成下凸包。

Part1/2. 核心思想

既然还有一个别称叫“带权二分”，“带权”即 附加权值。

定义附加权值为 c，并且给题目中所述的 “k 个……” 每一个的权值都附加 c。然后求出此时的最优答案（不考虑题目中“恰好 k 个的限制”）$f’(x)$ 以及对应的 x。
不难发现 $f’(x)=f(x)+cx$，因为 “x 个……” 每一个都附加了权值 c，所以多了一个 $cx$。

然后移一下项：$f(x)=-cx+f’(x)$！发现这是一个直线的解析式，$-c$ 为斜率，$f’(x)$ 为截距。

由于 $f(x)$ 的凸性质，可以得到 $f(x)$ 的切线的斜率与 $x$ 成单调性。当我们找到一个斜率 $-c$，满足其最优答案 $f’(x)$ 对应的 $x=k$，那么 $f’(x)-cx=f(x)=f(k)$ 就是我们要求的最优答案。

于是我们就可以 二分 $c$ 的权值，然后求出 $f’(x)$ 对应的 $x$，根据 $x$ 与 $k$ 的大小关系，调整 $c$ 的范围。

> Hint
现在还比较抽象，不妨先把不懂的放一放，之后看例题解析就明白了~

Part1/3. 栗子

假设 $f(x)$ 长下面这样：

png1

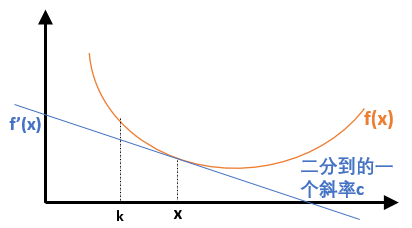
此时算出来的 $f’(x)$ 对应的 $x$ 大于 $k$，因此要让 $x$ 向左移，观察凸包，发现就是要让切线的斜率 $-c$（注意有负号）减小，即让切线变陡。

Part1/4. 算法正确性

由之前的式子 $f’(x)=f(x)+cx$，可知：由于我们求的是 $f’(x)$ 的最优值，那么减去 $cx$，一定是 $f(x)$ 的最优值。

会不会出现当 c 减小一点 x 就比 k 大，c 增大一点 x 就比 k 小（或者反过来）……反正就是二分不到 x=k？

但是由于 $f(x)$ 的凸性质，二分斜率一定可以判断出怎样调整斜率可以让 x 向 k 的方向移。唯一比较麻烦的情况就是三点共线……像下面这样：

png2

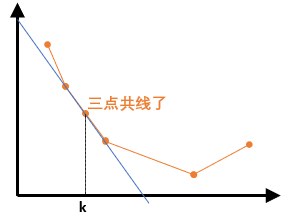
非常尴尬 事实上很有可能出现这种情况……二分的时候计算 $f’(x)$ 对应的 $x$，可能计算到 $k-1,k+1$，但是就是算不到 $k$。看似我们求不到 $f’(k)$，实际上正因为这几个点共线，我们只要求出那 3 个点的 $f’(x)$ 之一即可。

比如我们求得了 $f’(k-1)$，那么根据凸包，不难发现 $f(k)=f’(k-1)-ck$。照样能够算出来。

Part2. 例 - tree

要对题目中的 “恰好” 二字敏感……

Part2/1. 题面

有一个无向连通图，每条边有边权和颜色。边有黑白两色。
求在包含恰好 k 条白边的情况下的最小生成树，保证有解。

点数不超过 $50000$，边数不超过 $10^5$。

Part2/2. 解析

发现恰好二字，然后来研究一下 $f(x)$ 即“恰好有 $x$ 条白边的最小生成树”的性质。打表发现（不开玩笑……反正又不要你证明），$f(x)$ 满足下凸性质。然后就愉快地带权二分了！

二分一个附加值 c（就是切线的斜率），然后给每条白边都附加一个权值 c（白边的边权增加 c），跑一遍 Kruskal，在求出最小生成树 $f’(x)$ 的同时统计一下选的白边的数量 $x$。

再根据 $x,k$ 的大小关系，二分调整 c 的大小就好了。

> Tip
其实感性理解一下，当我们增大附加值 c 时，选择白边的代价增大，要使生成树代价小，白边被选的概率就会减小；反之减小 c 时，选择白边代价减小，被选的概率增大。

Part2/3. 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/*Lucky_Glass*/
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=5e4,M=1e5;

struct DSU{
	int fa[N+3];
	void Init(int n){
		for(int i=0;i<=n;i++)
			fa[i]=i;
	}
	int FindFa(int u){
		if(fa[u]==u) return u;
		return fa[u]=FindFa(fa[u]);
	}
	bool Merge(int u,int v){
		int fu=FindFa(u),fv=FindFa(v);
		if(fu==fv) return false;
		fa[fu]=fv;
		return true;
	}
}D_;
struct EDGE{
	int u,v,cst,typ;
	EDGE(){}
	EDGE(int _u,int _v,int _c,int _t):u(_u),v(_v),cst(_c),typ(_t){}
}E_[M+3];

int n,m,ned,ans;

bool cmpEDGE(const EDGE &cura,const EDGE &curb){
	if(cura.cst==curb.cst) return cura.typ<curb.typ;
	return cura.cst<curb.cst;
}
bool Check(int add){
	D_.Init(n);
	for(int i=1;i<=m;i++)
		if(E_[i].typ==0)
			E_[i].cst+=add;
	sort(E_+1,E_+1+m,cmpEDGE);
	int sum=0,wht=0;
	for(int i=1;i<=m;i++)
		if(D_.Merge(E_[i].u,E_[i].v)){
			sum+=E_[i].cst;
			wht+=!E_[i].typ;
		}
	for(int i=1;i<=m;i++)
		if(E_[i].typ==0)
			E_[i].cst-=add;
	ans=sum-wht*add;
	return wht>=ned;
}
int main(){
	scanf("%d%d%d",&n,&m,&ned);
	for(int i=1;i<=m;i++)
		scanf("%d%d%d%d",&E_[i].u,&E_[i].v,&E_[i].cst,&E_[i].typ);
	int adl=-200,adr=200;
	while(adl+1<adr){
		int adm=(int)floor((adl+adr)*0.5);
		if(Check(adm)) adl=adm;
		else adr=adm;
	}
	Check(adl);
	printf("%d\n",ans);
	return 0;
}

The End

Thanks for reading!

OI 的半期考试要来了 :)