感觉很熟悉,但是看到算法的时候又感觉比较陌生
可能是之前没学好 QwQ
# 流水调度问题
有 $n$ 件物品、两台机器 $A,B$。第 $i$ 件物品需要先在 $A$ 上加工 $a_i$ 个单位时间,再在 $B$ 上加工 $b_i$ 个单位时间。机器每次只能处理一件物品。
可以调整 $n$ 件物品的加工顺序,求最小时间。
# 算法理论
不难发现,最优的方案一定会使 $A,B$ 的“空闲”时间尽可能少。显然 $A$ 一定可以让它一直工作(直到所有物品在 $A$ 都加工完),于是只考虑 $B$ 的花费时间。
我们可以通过若干次交换相邻两件物品的操作顺序来得到最优操作顺序(交换法)。不妨设当前两个相邻的物品为 $\{a_1,b_1\},\{a_2,b_2\}$。
我们可以把 $\{a_1,b_1\}$ 排在前面的所有情况全都排出来,对应过来也就有了 $\{a_2,b_2\}$ 排在前面的所有情况:
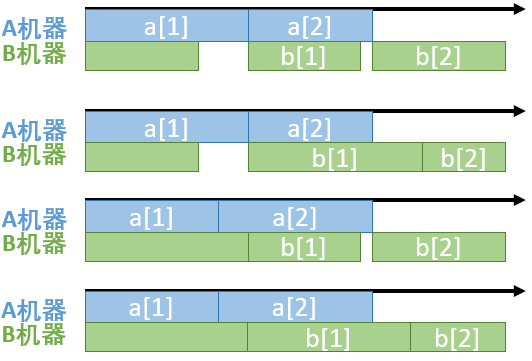
设 $\{a_1,b_1\}$ 在 A 上开始处理的时间为 $t_0$,$\{a_1,b_1\}$ 在 B 上开始处理的时间为 $\Delta t$,$\{a_2,b_2\}$ 在 B 上处理完的时间为 $T$。
可以发现 $T=\max\{a_1+a_2,a_1+b_1,\Delta t+b_1\}+b_2+t_0$。
那么同理,可以得到若先处理 $\{a_2,b_2\}$,则 $T’=\max\{a_1+a_2,a_2+b_2,\Delta t+b_2\}+b_1+t_0$。
于是分类讨论——讨论 $a_1,a_2,b_1,b_2$ 中的最小值
$a_1$ 为最小值:
可得 $a_1+a_2\le a_2+b_2$,于是 $T’=\max\{a_2+b_2,\Delta t+b_2\}+b_1+t_0$;
再变形,$T’=\max\{a_2+b_1,\Delta t+b_1\}+b_2+t_0$;
又可得 $a_1+b_1\le a_2+b_1$,$a_1+a_2\le a_2+b_1$;
所以 $\max\{a_1+a_2,a_2+b_1\}\le a_2+b_1$,则 $T\le T’$。
因此可以证明 $\{a_1,b_1\}$ 先处理一定不会更差。
$a_2$ 为最小值:
根据对称性,把 $a_1$ 最小的推导全部交换一下,可得结论:
$\{a_2,b_2\}$ 先处理一定不会更差。
$b_1$ 为最小值:
可得 $a_1+b_1\le a_1+a_2$,于是 $T’=\max\{a_1+a_2,\Delta t+b_1\}+b_2+t_0$;
再变形:$T=\max\{a_1+a_2+b_2,\Delta t+b_1+b_2\}+t_0$;
把 $T’$ 也变形一下:$T’=\max\{a_1+a_2+b_1,a_2+b_2+b_1,\Delta t+b_1+b_2\}+t_0$;
因为 $a_1+a_2+b_1\le a_1+a_2+b_2$,$a_2+b_2+b_1\le a_1+a_2+b_2$;
所以 $T\ge T’$,则 $\{a_2,b_2\}$ 先处理一定不会更差。
$b_2$ 为最小值:
同理,根据对称性,$\{a_1,b_1\}$ 先处理一定不会更差。
# 设计贪心
从相邻两个考虑到整体——
- 假如某个 $a_i$ 是 $a_1,a_2,\dots,a_n,b_1,b_2,\dots,b_n$ 的最小值,则 $\{a_i,b_i\}$ 根据之前的分析,可以一直往前挪,即应该第一个处理;
- 假如某个 $b_i$ 是 $a_1,a_2,\dots,a_n,b_1,b_2,\dots,b_n$ 的最小值,则 $\{a_i,b_i\}$ 根据之前的分析,一直往后挪,即应该最后一个处理;
因此,我们把所有 $a_1,a_2,\dots,a_n,b_1,b_2,\dots,b_n$ 作为 $S$,每次取出 $S$ 的最小值,若最小值是 $a_i$,则把 $\{a_i,b_i\}$ 放在前面;若是 $b_i$,则把 $\{a_i,b_i\}$ 放在后面。然后在 $S$ 中删掉 $a_i,b_i$。
一直处理到结束。
伪代码如下: