7
# 题面
A. 信心(confidence)
有 $n$ 个整数 $x_1$ 到 $x_n$,其中第 $i$ 个整数 $x_i$ 满足限制:$x_i\in[l_i,r_i]$。
给定 $[l_i,r_i]$,求 $\sum\limits_{i=1}^nx_i^2$ 有多少种取值。
数据规模:$1\le n,l_i,r_i\le100$。
B. 传统(tradition)
有一台生产硬币的机器。它总共可以生产 $n$ 种硬币,第 $i$ 种硬币价值 $v_i$。
这台机器每天可以生产若干种硬币,但是同种硬币只能生产一枚,且对于第 $i$ 种硬币,不能连续 $d_i$ 天生产这种硬币。
另外,机器最多连续工作 $k$ 天。在机器不工作的那天不能生产任何硬币。
求 $m$ 天最多能够生产总价值为多少的硬币。
数据规模:$1\le m\le10^9$,$1\le n\le1000$,$2\le k\le 1000$,$2\le d[i]\le10^9$,$1\le v[i]\le1000 $
C. 改编(adaptation)
3只兔子在一条无限长的树桩上游戏,树桩编号为 $\dots,-2,-1,0,1,2,\dots$。一开始树桩 $a,b,c$ 上有兔子。
一轮游戏的规则为:选定一只兔子A和另一只兔子B,记剩下那只兔子为C;则A以B的位置为对称轴跳到对称的点上,要求不会跳过C(到达的位置也不能有兔子)。
现在进行 $k$ 轮游戏,再给出终止状态——在树桩 $a’,b’,c’$ 上有兔子。问有多少种不同的游戏的方案。两种方案不同当且仅当存在至少一个中间局面不同。
数据规模:$1\le k\le100$,所有位置的绝对值不超过 $10^{18}$。
# 解析
A. 信心(confidence)
我们发现这道题并没有一个非常好的思路,就一个 $O(n^5)$ 的 DP。也就是 f[i][S] 表示 $\sum\limits_{j=1}^ix_j^2=S$ 是否可能,其中 $S$ 的规模是 $O(n^3)$ 的(存状态就滚动数组优化第一维)。转移也非常暴力:枚举 $x_i\in[l_i,r_i]$,然后类似背包问题转移。
顶多想到转移可以用 FFT/NTT 稍微优化它一下……理论复杂度 $O(n^4\log n)$,实测 TLE 爆零了 :(
然后我们发现这个DP其实是一个bool状态的……值为 false/true……0/1——二进制?如果对 bitset 熟悉的话,它的超级小的常数可以帮上大忙。
转移用左移来实现,赋值用按位或实现。
复杂度 $O(n^5w)$,比 $10^8$ 稍微大一点,开上 O2 没有问题。
B. 传统(tradition)
(坑在这儿,不会再填了 QwQ)
C. 改编(adaptation)
现场有人做过跳跳棋这道题,然后差一点 AC……
我们可以把一轮游戏分为两类:
- 中间往外跳
- 两边往中间跳
对于一个局面 $a,b,c$,$b$ 一定可以往两边跳,而 $a$ 和 $c$ 最多只有一个能往中间跳:
- $b-a>c-b$:$c$ 可以往中间跳;
- $b-a<c-b$:$a$ 可以往中间跳;
- $b-a=c-b$:两边都不能往中间跳。
这像什么?画张图:
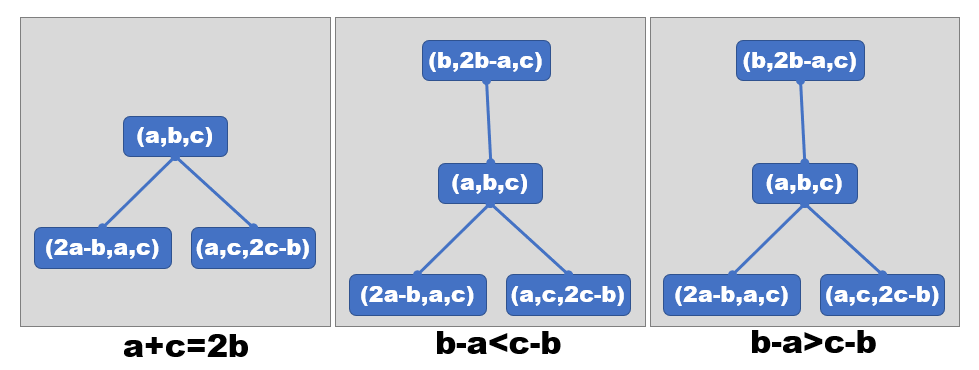
一个二叉树?准确的说,一个无限大的二叉树森林。
那么我们就是要求有多少条从 $(a,b,c)$ 到 $(a’,b’,c’)$ 的长度为 $k$ 的路径(边可以重复)。
我们先求在二叉树上 $(a,b,c)$ 和 $(a’,b’,c’)$ 的 LCA,并且求出它们分别与 LCA 的距离;当然如果它们不在一棵二叉树上就不存在这样的路径。
Hint. 求LCA直接暴力枚举两个状态分别向上爬多少步就行,因为限制了路径长度,所以如果有解,那 LCA 肯定最多只用向上爬 $k$ 步。也就是 $O(k^2)$ 计算 LCA。
然后定义 DP 状态:f[i][j][l] 表示“当前状态与 LCA 的距离为 i,结束状态与 LCA 的距离为 j,长度为 l 的路径的方案数”
Tab. 定义里的 LCA 是指当前状态与结束状态的 LCA,不是起始状态与结束状态的 LCA!
考虑转移,即当前状态向父亲/两个儿子移动,分3种情况:
- i>0:此时无论当前状态怎么移动,LCA都不会变
- 向父亲移动
f[i][j][l]+=f[i-1][j][l-1]
- 向任意一个儿子移动
f[i][j][l]+=f[i+1][j][l-1]*2
- i=0且j>0:此时当前状态就是 LCA,注意当前状态移动后 LCA 的变化!
- 向父亲移动
f[0][j][l]+=f[0][j+1][l-1]
- 向结束状态的子树移动
f[0][j][l]+=f[0][j-1][l-1]
- 向另一个子树移动
f[0][j][l]+=f[1][j][l-1]
- i=0且j=0:此时两个状态重合,仍然注意 LCA 的变化!
- 向父亲移动
f[0][0][l]+=f[0][1][l-1]
- 向任意儿子移动
f[0][0][l]+=2*f[1][0][l-1]
那么就用记忆化搜索即可,可以加上几个剪枝,详见代码。
# 源代码
A. confidence.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include<bitset>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100,VAL=1e6+5;
bitset<VAL> dp[2];
int n;
int RI(){
int a=0,c=getchar();
while(c<'0' || '9'<c) c=getchar();
while('0'<=c && c<='9'){
a=(a<<1)+(a<<3)+c-'0';
c=getchar();
}
return a;
}
int main(){
freopen("confidence.in","r",stdin);
freopen("confidence.out","w",stdout);
n=RI();
dp[0]=1;
for(int i=1;i<=n;i++){
dp[i&1]=0;
int lef=RI(),rig=RI();
for(int k=lef;k<=rig;k++)
dp[i&1]|=dp[i&1^1]<<(k*k);
}
printf("%d\n",(int)dp[n&1].count());
return 0;
}
|
B. tradition.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1000,VAL=1e6,M=1e6+100;
int day,bet,n;
int ibet[N+3],ival[N+3],val[N+3];
long long dp[M+N+3];
int RI(){
int a=0,c=getchar();
while(c<'0' || '9'<c) c=getchar();
while('0'<=c && c<='9'){
a=(a<<1)+(a<<3)+c-'0';
c=getchar();
}
return a;
}
int main(){
freopen("tradition.in","r",stdin);
freopen("tradition.out","w",stdout);
day=RI();bet=RI();n=RI();
for(int i=1;i<=n;i++)
ival[i]=RI();
for(int i=1;i<=n;i++)
ibet[i]=RI();
day++;
for(int l=2;l<=bet;l++){
for(int i=1;i<=n;i++)
val[l]+=((l-1)-(l-1)/ibet[i])*ival[i];
dp[l]=val[l];
}
for(int i=0;i<=M;i++)
for(int j=bet/2+1;j<=bet;j++)
dp[i+j]=max(dp[i+j],dp[i]+val[j]);
long long ans=0;
int mx=1;
for(int i=1;i<=bet;i++)
if(1ll*val[i]*mx>1ll*val[mx]*i)
mx=i;
for(int i=0;i<=day && i<=M;i++)
ans=max(ans,dp[i]+1ll*((day-i)/mx)*val[mx]);
printf("%lld\n",ans);
return 0;
}
|
C. adaptation.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=110,MOD=1e9+7;
int Sub(int a,int b){return a-b<0? a-b+MOD:a-b;}
int Add(int a,int b){return a+b>=MOD? a+b-MOD:a+b;}
int Mul(int a,int b){return 1ll*a*b%MOD;}
struct STATUS{
ll a,b,c;
bool MoveFa(){
if(a+c==b*2) return false;
if(b-a>c-b) c=2*b-c,swap(b,c);
else a=2*b-a,swap(a,b);
return true;
}
ll RI(){
ll num=0;int sig=1,ch=getchar();
while(ch<'0' || '9'<ch) sig=ch=='-'? -1:sig,ch=getchar();
while('0'<=ch && ch<='9') num=(num<<1)+(num<<3)+ch-'0',ch=getchar();
return num*sig;
}
void Read(){
a=RI();b=RI();c=RI();
if(a>b) swap(a,b);
if(a>c) swap(a,c);
if(b>c) swap(b,c);
}
bool operator ==(STATUS B){return a==B.a && b==B.b && c==B.c;}
}S,T;
int cas,rot,stp,dS,dT;
int f[N+3][N+3][N+3];
bool LCA(){
rot=stp;
STATUS copS,copT=T;
for(int i=0;i<=stp;i++)
if(!copT.MoveFa()){
rot=i;
break;
}
copS=S;
for(int i=0;i<=stp;i++){
copT=T;
for(int j=0;j<=stp;j++){
if(copT==copS){
dS=i;dT=j;
return true;
}
copT.MoveFa();
}
copS.MoveFa();
}
return false;
}
int DP(int DS,int DT,int LE){
if(f[DS][DT][LE]>=0) return f[DS][DT][LE];
if(DS+DT>LE || DT>rot) return 0;
int &ret=f[DS][DT][LE]=0;
if(DS>0) ret=Add(DP(DS-1,DT,LE-1),Mul(DP(DS+1,DT,LE-1),2));
else if(DT>0) ret=Add(DP(0,DT+1,LE-1),Add(DP(1,DT,LE-1),DP(0,DT-1,LE-1)));
else ret=Add(DP(0,1,LE-1),Mul(DP(1,0,LE-1),2));
return ret;
}
int main(){
freopen("adaptation.in","r",stdin);
freopen("adaptation.out","w",stdout);
memset(f,-1,sizeof f);f[0][0][0]=1;
S.Read();T.Read();
scanf("%d",&stp);
if(LCA()) printf("%d\n",DP(dS,dT,stp));
else printf("0\n");
return 0;
}
|
THE END
Thanks for reading!
