OI - 魔法阵(洛谷团队赛) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI - 魔法阵(洛谷团队赛)

发表于 分类于 Valine：

一道令人不得不佩服的二合一题目
（然而“二合一”的两个部分我一个都没弄出来）

# 题面

点击展开/折叠题面

著名炼金术士威廉正在完成他秘密计划的最后一步。

威廉一开始有一个已经固定的长度为 $n$ 的序列 $a_i=i,i\in[0,n-1]$ 一个自己设定的一个长度为 $n$ 的序列 $b_i$。

按照古书上的记载，威廉现在可以对这两个序列施展魔法，施展一次魔法可以使这个序列向右循环位移一次，即序列中最后一个位置上的数字移到第一个数字的前面，其余的数字的下标依次加一。如果威廉对某个序列 $z$ 施展了 $i$ 次魔法，那么我们将得到的结果序列设为 $Magic(z,i)$。

现在，威廉需要用若干个相同的 $a$ 序列和 $b$ 序列得到他最终需要的魔法阵。

具体来说，威廉需要先准备好两个矩阵 $A$ 和 $B$，其中矩阵 $A$ 的第 $i,i\in[0,n-1]$ 行是 $Magic(a,i)$，同理，矩阵 $B$ 的第 $i,i\in[0,n-1]$ 行是 $Magic(b,i)$。

那么威廉最终要得到的魔法阵就是 $C=A\times B$。

当然，这些魔法对威廉来说实在是太简单了，因此他想对他的学生——你提出 $q$ 个询问或操作来检验一下自己的教学成果:

  • 0 x0 y0 x1 y1：查询魔法阵中左上角为$(x_0,y_0)$，右下角为$(x_1,y_1)$的子矩形的 $C_{i,j}^t$ 之和模 $n$ 的结果，注意 $t$ 是一开始给定的常数。
  • 1 i k p：对魔法阵 $C$ 中的第 $i$ 行从左到右依次加上 $Magic(a,p)$ 中的每个数字的 $k$ 倍。
  • 2 j k p：对魔法阵 $C$ 中的第 $j$ 列从上到下依次加上 $Magic(a,p)$ 中的每个数字的 $k$ 倍。
  • 3 x0 y0 x1 y1：查询魔法阵中左上角为$(x_0,y_0)$ ，右下角为$(x_1,y_1)$的子矩形的$C_{i,j}$之和模 $n$ 的结果。

威廉当然知道这有些难为反应有些迟钝的你，因此他的第一类询问只会在一开始提出，一旦提出了其他询问或操作，之后就不会再出现。

你能成功回答威廉提出的所有问题吗？

# 解析

看到“第一类询问只会在一开始提出”就知道这道题大概是二合一……

在分类处理两个部分前，需要证明大小两个性质。

第一个小性质

$$\{C_{i,0},C_{i,1},\dots,C_{i,n-1}\}=Magic(\{C_{0,0},C_{0,1},\dots,C_{0,n-1}\},i)$$

证明略，展开即可。

第二个重要性质

设 $\sum b=S$，则 $\{C_{i,0},C_{i,1},\dots,C_{i,n-1}\}$ 在模 $n$ 意义下是公差为 $S$ 的等差数列。

$$ \begin{aligned} C_{i,j}&=\sum_kA_{i,k}B_{k,j}\\ C_{i,j+1}&=\sum_kA_{i,k}B_{k,j+1}\\ &=\sum_kA_{i,k}B_{k-1,j}\\ &=\sum_kA_{i,k+1}B_{k,j} \end{aligned} $$

因为 $A_{i,k+1}=A_{i,k}+1$，所以 $C_{i,j+1}-C_{i,j}=S$。

（考试的时候两个都发现了，但是第二个没发现重点）

这样就可以先 $O(n)$ 算出 $C_{0,0}$，然后再利用性质二每次加 $S$ 得到 $C_{0,i}$；因为性质一，就相当于求到了整个 $C$ 矩阵。

- 询问1

根据性质一，我们可以推得矩阵 $C$ 的主对角线方向上的数字是相等的。

把从左下角的主对角线到右上角的主对角线依次标号为 $1\sim 2n-1$，如下图：

然后看询问框出的一个矩形：

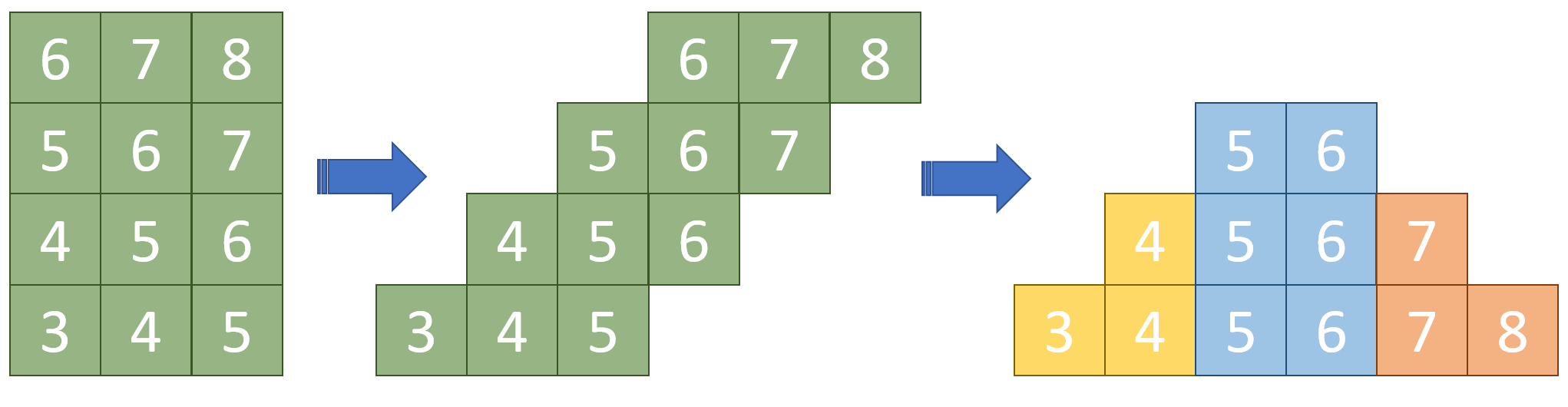
于是套路维护前后缀三角形后缀（黄色、红色区域）和普通前缀和（蓝色区域）。

就是写代码的时候注意下标。

- 询问2

发现两种操作都是在行或列上加一个等差数列，而且原来矩阵 $C$ 的每一行/列也是等差数列。

于是可以维护每一行的等差数列的首项以及公差；和每一列的修改新增的等差数列的首项及公差（一定是修改的等差数列，避免计算重复）。

因为等差数列对应项求和得到的数列也是等差数列，所以可以首项、公差分别求和，用树状数组就可以了。

详见代码，思路清晰，比较好写。

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<cassert>
#include<algorithm>
using namespace std;

inline int Read(){
	register int r=0,c=getchar();
	while(c<'0' || '9'<c) c=getchar();
	while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
	return r;
}

const int N=5e5+10;
#define ci const int &
#define lowbit(x) ((x)&(-(x)))

int n,t,m,sumB;
int aryB[N],aryC[N<<1],powC[N<<1];
int preC[N<<1],sufC[N<<1],sumC[N<<1];
int trolA[N],trolB[N],tcolA[N],tcolB[N];
//A: a0 / B: b -> sum[1~i]=i*a0+i*(i-1)/2*b

inline int Add(ci a,ci b){return a+b>=n? a+b-n:a+b;}
inline int Sub(ci a,ci b){return a-b<0? a-b+n:a-b;}
inline int Mul(ci a,ci b){return 1ll*a*b%n;}
inline int Pow(int a,int b){int r=1;while(b){if(b&1)r=Mul(r,a);a=Mul(a,a);b>>=1;}return r;}
inline int Id(ci x,ci y){return n-(x-y);}
inline int SumPre(ci l,ci r){return Sub(Sub(preC[r],preC[l-1]),Mul(l-1,Sub(sumC[r],sumC[l-1])));}
inline int SumSuf(ci l,ci r){return Sub(Sub(sufC[l],sufC[r+1]),Mul(2*n-1-r,Sub(sumC[r],sumC[l-1])));}
inline void Update(int *tre,int pos,ci key){
	pos++;
	while(pos<=n){
		tre[pos]=Add(tre[pos],key);
		pos+=lowbit(pos);
	}
}
inline int Query(int *tre,int pos){
	pos++;
	int ret=0;
	while(pos){
		ret=Add(ret,tre[pos]);
		pos-=lowbit(pos);
	}
	return ret;
}
int main(){
	n=Read(),t=Read(),m=Read();
	for(int i=0;i<n;i++) sumB=Add(sumB,aryB[i]=Read());
	for(int i=0,j=0;i<n;i++,j=(j==0? n-1:j-1))
		aryC[0]=Add(aryC[0],Mul(i,aryB[j]));
	powC[0]=Pow(aryC[0],t);
	for(int i=1;i<n*2;i++){
		aryC[i]=Add(aryC[i-1],sumB);
		powC[i]=Pow(aryC[i],t);
		//printf("%d ",powC[i]);
	}
	//printf("\n");
	for(int i=1;i<n*2;i++){
		sumC[i]=Add(sumC[i-1],powC[i]);
		preC[i]=Add(preC[i-1],Mul(i,powC[i]));
	}
	for(int i=2*n-1;i>0;i--)
		sufC[i]=Add(sufC[i+1],Mul(2*n-i,powC[i]));
	for(int i=0,j=n;i<n;i++,j--){
		Update(trolA,i,aryC[j]);
		Update(trolB,i,sumB);
		//printf("rol %d: %dx+%d\n",i,aryC[j],sumB);
	}
	while(m--){
		int cmd=Read();
		switch(cmd){
			case 0:{
				int x0=Read(),y0=Read(),x1=Read(),y1=Read(),r=x1-x0+1,c=y1-y0+1;
				int p1=Id(x1,y0),p2=p1+min(r,c),p4=Id(x0,y1),p3=p4-min(r,c);
				//[p1,p2),[p2,p3],(p3,p4]
				printf("%d\n",Add(Add(SumPre(p1,p2-1),SumSuf(p3+1,p4)),Mul(min(r,c),Sub(sumC[p3],sumC[p2-1]))));
				break;
			}
			case 1:{
				int i=Read(),k=Read(),p=Mul(n-Read(),k);
				//printf("rol %d : add %dx+%d\n",i,k,p);
				Update(trolA,i,p);
				Update(trolB,i,k);
				break;
			}
			case 2:{
				int j=Read(),k=Read(),p=Mul(n-Read(),k);
				//printf("col %d : add %dx+%d\n",j,k,p);
				Update(tcolA,j,p);
				Update(tcolB,j,k);
				break;
			}
			case 3:{
				int x0=Read(),y0=Read(),x1=Read(),y1=Read(),r=x1-x0+1,c=y1-y0+1;
				int rola0=Sub(Query(trolA,x1),Query(trolA,x0-1)),rolb=Sub(Query(trolB,x1),Query(trolB,x0-1));
				rola0=Add(rola0,Mul(rolb,y0));
				int cola0=Sub(Query(tcolA,y1),Query(tcolA,y0-1)),colb=Sub(Query(tcolB,y1),Query(tcolB,y0-1));
				cola0=Add(cola0,Mul(colb,x0));
				//printf("? %d %d %d %d\n",rola0,rolb,cola0,colb);
				printf("%d\n",Add(Add(Mul(rola0,c),Mul(rolb,int(c*(c-1ll)/2%n))),Add(Mul(cola0,r),Mul(colb,int(r*(r-1ll)/2%n)))));
				break;
			}
		}
	}
	return 0;
}

THE END

Thanks for reading!

> Linked 樱花绽放时-网易云