前行 - 2020校内常规测试Ⅱ | Lucky_Glass's Blog

以心为名，名为爱惜

0%

前行 - 2020校内常规测试Ⅱ

发表于 分类于 Valine：

又是搬来的题，但是不是教练搬的了 awa
因为 T1 不难，考场上就想出来了，这里就不写了……

# 题目

B. 谎言(lie)

有 $n$ 个选手，两两之间进行一场比赛，总共 $\frac{n(n-1)}{2}$ 场。一个选手的得分是他与其他选手进行的比赛中，他获胜的次数（获胜不具有传递性，也就是说 A 战胜 B，B 战胜 C，但 A 不一定战胜 C）。

现给定每个选手的得分 $a_1,a_2,\dots,a_n$，判断是否可能出现这种得分情况。

多组数据（共 $T$ 组）。

数据规模：$1\le T\le50,1\le n\le40000,0\le a_i\le n-1$。

C. 牢不可破的联盟(union)

有 $n$ 个点形成一棵树，每个点有一个颜色 $c_i$，共有 $m$ 种颜色（保证每种颜色都出现）。

选出一个颜色集合 $S$，使得对于任意 $u,v$ 满足 $c_u,c_v\in S$，存在 $u$ 到 $v$ 只经过颜色在 $S$ 中的点的路径。求 $|S|$ 的最小值。

数据规模：$1\le n\le2\times10^5;1\le m\le n$。

# 解析

B. 谎言(lie)

首先可以知道：必须满足 $\sum\limits_{i=1}^{n}a_i=\frac{(n-1)n}{2}$。之后再来处理别的情况。

假如 $n$ 没有这么大，应该怎么做？比如网络流？建 $\frac{(n-1)n}2$ 个点 $X_i$ 表示每场比赛，$n$ 个点 $Y_i$ 表示每个选手。源点向 $X_i$ 连容量为 1 的边；$X_i$ 向对应的两个选手的点 $Y_i$ 连容量为 1 的边；$Y_i$ 向汇点连容量为 $a_i$ 的边。

这样的话，$X_i$ 的流量往哪个方向流，就表示哪个选手获胜，而 $X_i$ 流出的流量就是他获胜的次数。显然，当网络流流满就意味着有合法方案。

但是虽然网络流复杂度玄学，但是 $n$ 这么大显然过不了。

注意到这里的网络流建图就是个二分图，而且也非常像二分图匹配，只是 $Y_i$ 不满足“只匹配一条边”。我们不妨把 $Y_i$ 拆成 $a_i$ 个点，不就变成二分图匹配了？

当然这样肯定不能直接二分图匹配，要找一些规律。我们知道，只有二分图有完美匹配，就说明有合法方案。那么判断二分图是否有完美匹配有个重要的定理——Hall定理。

> 定理内容

一个二分图有完美匹配的充要条件是：定义一个点集 $S$ 的邻集是 $H(S)$，对于任意一个 $S\subseteq X$ 或 $S\subseteq Y$（$X,Y$ 是二分图的两个部），满足 $|H(S)|\ge |S|$。

不难发现，在这道题构建的二分图中，对于 $S\subseteq Y$，一定有 $|H(S)|\ge |S|$，因为 $Y$ 中的每个点都连了 $X$ 的 $n-1$ 个点。于是我们需要判断对于 $S\subseteq X$ 是否满足 Hall 定理的要求。

但是我们对 $S\subseteq X$ 的 $|H(S)|$ 并不好分析，于是考虑现在知道 $H(S)$，判断 $S$ 是否满足条件。显然一个选手拆分出的 $a_i$ 个点要么都不在 $H(S)$ 中，要么都在（根据建图方法可知）。于是 $|H(S)|$ 可以表示为：

$T$ 就是选手集合的一个子集。而对应的 $|S|$ 的意义就是 $T$ 中的选手两两比赛的比赛场数，于是 $|S|=\frac{|T|(|T|-1)}2$。那么 $|S|\le |H(S)|$ 这个条件就变为：

对于 $T_1,T_2$，如果 $|T_1|=|T_2|$，则只要 $\min\{\sum\limits_{i\in T_1}a_i,\sum\limits_{i\in T_2}a_i\}\ge \frac{|T|(|T|-1)}{2}$ 即可。所以对于每个 $|T|$，找到 $\sum\limits_{i\in T}a_i$ 的最小值——显然一开始输入过后把 $a_i$ 排序，前缀和一下，前缀和第 $i$ 个就是 $|T|=i$ 时的 $\sum\limits_{i\in T}a_i$ 的最小值了。

C. 牢不可破的联盟(union)

为了方便表示，设 $S_i$ 表示颜色为 $i$ 的点的集合。

先考虑暴力一点的做法——如果选择颜色 $i$ ，则对于任意两个 $u,v\in S_i$，它们的路径上的点的颜色一定要选。于是我们 $n^2$ 暴力DFS，对于每种颜色，求出如果要让它的所有点连通，还必须选哪些颜色。

然后对 $m$ 种颜色建一张新图，如果颜色 $i$ 的点想要联通必须也选择颜色 $j$ ，则连有向边 $i\to j$。

这样就把“依赖关系”找到了。如果颜色 $i,j$ 在一个强连通分量里，那么 $i,j$ 必须同时选或同时不选。于是答案就是 没有出边的强连通分量的最小大小。

我们发现这个算法的缺点有两个：①建图的复杂度 $O(n^2)$；②新图的边数 $O(m^2)$。

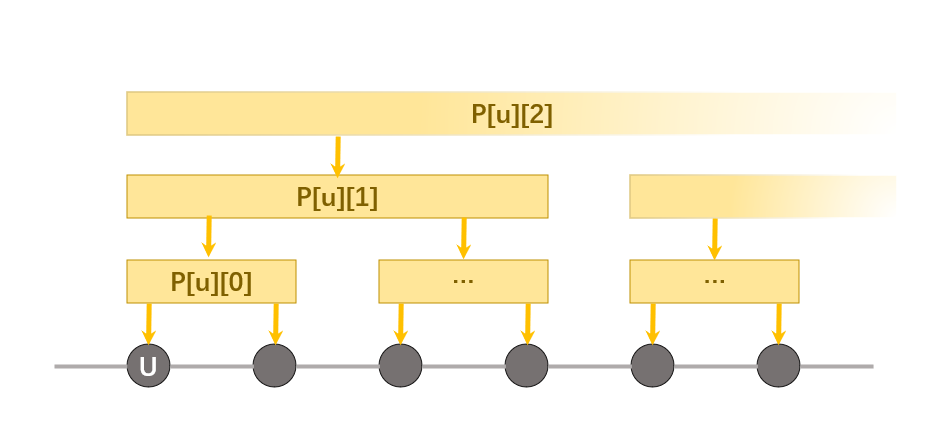
由于原图是一棵树，就有很多好玩的性质，比如可以倍增。就像 ST 表那样，或者说像线段树优化建图那样：

png1

那么这样新图的点数边数都变成了可接受的 $O(n\log n)$。

再考虑建图。因为已经有倍增算法的辅助，可以迅速地连接两点间路径上的所有点（代码实现时不是连接点，而是连接点的颜色）；我们发现，当我们在对颜色 $i$ 建图的时候，需要的只是 $S_i$ 中的点。于是这样只需要原树中一个子点集的问题，可以用虚树解决，则建图复杂度也是 $O(n\log n)$。

# 源代码

B. lie.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=40000;

int val[N+3];
int n,cas;

int RI(){
	int a=0,c=getchar();;
	while(c<'0' || '9'<c) c=getchar();
	while('0'<=c && c<='9'){
		a=(a<<1)+(a<<3)+c-'0';
		c=getchar();
	}
	return a;
}
int main(){
	freopen("lie.in","r",stdin);
	freopen("lie.out","w",stdout);
	cas=RI();
	while(cas--){
		n=RI();
		int tot=0;
		for(int i=1;i<=n;i++)
			tot+=val[i]=RI();
		sort(val+1,val+n+1);
		bool fail=tot!=n*(n-1)/2;
		for(int i=1,sum=0;i<=n && !fail;i++){
			sum+=val[i];
			if(sum<i*(i-1)/2)
				fail=true;
		}
		if(fail) printf("cake is lie.\n");
		else printf("cake is not lie.\n");
	}
	return 0;
}

C. union.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
/*Lucky_Glass*/
#include<stack>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=2e5+3,M=N*22;

struct EDGE{
	int to;EDGE *nxt;
	EDGE(){}
	EDGE(int _t,EDGE *_n):to(_t),nxt(_n){}
};
struct GRAPH{
	EDGE edg[N*2+3],*head[N+3],*ncnt;
	GRAPH(){ncnt=edg;}
	void AddEdge(int u,int v){
		EDGE *p=++ncnt,*q=++ncnt;
		*p=EDGE(v,head[u]);head[u]=p;
		*q=EDGE(u,head[v]);head[v]=q;
	}
	EDGE* operator [](int id){return head[id];}
}Gr;

int n,m,ndfn,nid,nscc;
int col[N];
int id[N][20],anc[N][20],dfn[M],dep[N],lg2[N],low[M],scc[M],siz[M];
bool instk[M];
vector<int> lnk[M],in[N];
stack<int> stk;

int RI(){
	int a=0,c=getchar();
	while(c<'0' || '9'<c) c=getchar();
	while('0'<=c && c<='9'){
		a=(a<<1)+(a<<3)+c-'0';
		c=getchar();
	}
	return a;
}
void AddEdge(int u,int v){lnk[u].push_back(v);}
void DFS(int u,int fa){
	dfn[u]=++ndfn;
	dep[u]=dep[fa]+1;
	anc[u][0]=fa;
	if(fa){
		id[u][0]=++nid;
		AddEdge(id[u][0],col[fa]);
		AddEdge(id[u][0],col[u]);
	}
	for(int i=1;i<20;i++){
		anc[u][i]=anc[anc[u][i-1]][i-1];
		if(anc[u][i]){
			id[u][i]=++nid;
			AddEdge(id[u][i],id[u][i-1]);
			AddEdge(id[u][i],id[anc[u][i-1]][i-1]);
		}
	}
	for(EDGE *it=Gr[u];it;it=it->nxt){
		int v=it->to;
		if(v==fa) continue;
		DFS(v,u);
	}
}
bool cmpDFN(int a,int b){return dfn[a]<dfn[b];}
int LCA(int u,int v){
	if(dep[u]<dep[v]) swap(u,v);
	for(int i=19;i>=0;i--)
		if(dep[anc[u][i]]>=dep[v])
			u=anc[u][i];
	if(u==v) return u;
	for(int i=19;i>=0;i--)
		if(anc[u][i]!=anc[v][i]){
			u=anc[u][i];
			v=anc[v][i];
		}
	return anc[u][0];
}
void Link(int co,int u,int v){
	if(u==v) return;
	if(dep[u]<dep[v]) swap(u,v);
	//dep[u]>dep[v]
	int len=dep[u]-dep[v],lgl=lg2[len],de=dep[v]+(1<<lgl);
	AddEdge(co,id[u][lgl]);
	for(int i=19;i>=0;i--)
		if(dep[anc[u][i]]>=de)
			u=anc[u][i];
	AddEdge(co,id[u][lgl]);
}
void Insert(int u,int co){
	if(!stk.empty()){
		int lca=LCA(u,stk.top());
		if(lca!=stk.top()) //not in the subtree
			while(true){
				int v=stk.top();stk.pop();
				if(stk.empty() || dfn[stk.top()]<dfn[lca]){  //pop all points on the path
					//link v-lca
					Link(co,v,lca);
					stk.push(lca);
					break;
				}
				else{
					//link v-top
					Link(co,v,stk.top());
					if(lca==stk.top()) break;
				}
			}
	}
	stk.push(u);
}
void Tarjan(int u){
	dfn[u]=low[u]=++ndfn;
	stk.push(u);instk[u]=true;
	for(int i=0,li=lnk[u].size();i<li;i++){
		int v=lnk[u][i];
		if(!dfn[v]){
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else
			if(instk[v])
				low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u]){
		nscc++;
		int tmp=0;
		do{
			tmp=stk.top();stk.pop();
			scc[tmp]=nscc;
			siz[nscc]+=(tmp<=m);
			instk[tmp]=false;
		}while(tmp!=u);
	}
}
int main(){
//	freopen("input.txt","r",stdin);
	freopen("union.in","r",stdin);
	freopen("union.out","w",stdout);
	n=RI();nid=m=RI();
	for(int i=1;i<n;i++)
		Gr.AddEdge(RI(),RI());
	for(int i=1;i<=n;i++)
		in[col[i]=RI()].push_back(i);
	DFS(1,0);
	for(int i=2;i<=n;i++) lg2[i]=lg2[i>>1]+1;
	for(int co=1;co<=m;co++){
		sort(in[co].begin(),in[co].end(),cmpDFN);
		for(int i=0,li=in[co].size();i<li;i++)
			Insert(in[co][i],co);
		while(true){
			int u=stk.top();stk.pop();
			if(stk.empty()) break;
			else Link(co,u,stk.top());
		}
	}
	memset(dfn,0,sizeof dfn);
	ndfn=0;
	for(int u=1;u<=nid;u++)
		if(!dfn[u])
			Tarjan(u);
	int ans=m;
	for(int u=1;u<=nid;u++)
		for(int i=0,li=lnk[u].size();i<li;i++){
			int v=lnk[u][i];
			if(scc[v]!=scc[u])
				siz[scc[u]]=m+1;
		}
	for(int i=1;i<=nscc;i++)
		ans=min(ans,siz[i]);
	printf("%d\n",ans-1);
	return 0;
}

THE END

Thanks for reading!