开始着手补字符串这个大坑
# 前缀函数
方便起见,对于字符串 $S$ 定义 $S(l,r)$ 表示 $S$ 的子串 $S_{l}S_{l+1}\dots S_r$。
对于一个长度为 $n$ 的字符串 $S=S_0S_1\dots S_{n-1}$,定义 $\pi[i]$ ($i\in[0,n-1]$)表示以 $i$ 结尾的最长真后缀使得该后缀同时为 $S$ 的一个前缀。
换句话说 $S(0,\pi[i]-1)=S(i-\pi[i]+1,i)$。
在此定义下,不难发现 $\pi[0]=0$(注意是真后缀)。
# 求$\pi$ - KMP
在过去所学习的 KMP 中,用到了一种 fail 指针,这样的指针为 AC 自动机的实现提供了一个基础。但是对于 KMP 算法,还有一种基于前缀函数的性质的实现。
这两种实现都是在求解 $\pi$ 函数,只是方法不同。应该基于前缀函数的理解更为简单。
同样,我们希望用到尽可能多的已经计算过的值。假设我们知道了 $\pi[0\dots i-1]$,希望求出 $\pi[i]$。
首先 $\pi[i]$ 最大为 $\pi[i-1]+1$,就相当于直接在上一个后面加上 $S_i$。于是我们定义一个指针 $j=\pi[i-1]$:
如果 $S_j=S_i$(注意到 $S$ 是从 $0$ 开始的),则 $\pi[i]=j+1$;
否则我们需要挪动 $j$ —— 挪到下一个最长的可能匹配的位置:
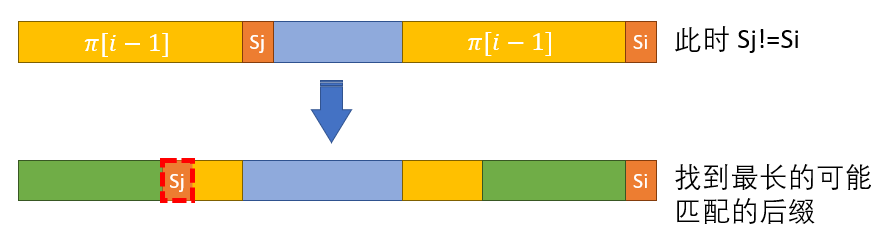
我们发现最长的可能匹配的后缀(绿色部分)其实是 $\pi[\pi[i-1]-1]$,为什么呢?
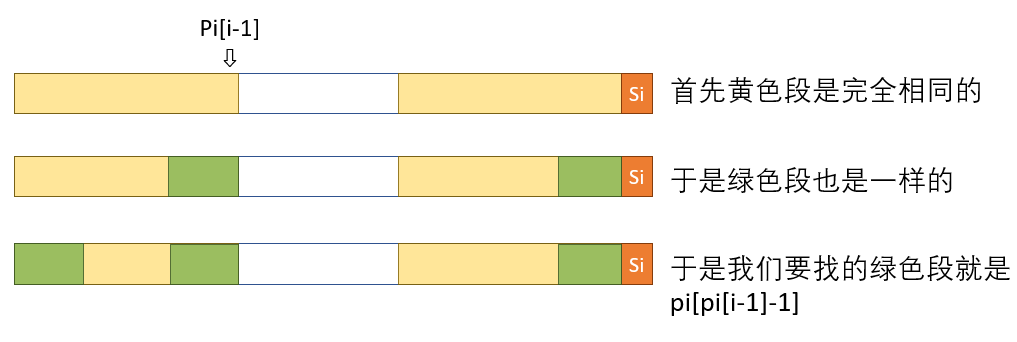
于是 $j$ 只要一直沿着 $\pi$ 函数往回跳——直到跳到 $S_j=S_i$ 或者 $j=0$(意味着可能 $S_i$ 与什么都不能匹配,或是 $\pi[i]=1$,即只匹配了 $S_i$ 一个字符)。
# 伪代码
# 复杂度
KMP 的复杂度是 $O(n)$ 的,无论怎样实现。其复杂度决定于 $j$ 指针的移动。
为什么是 $O(n)$ 呢?之前我以为是因为 $j$ 指针沿着 $\pi$ 跳回去,可以节省复杂度,但是显然不是,因为完全可以构造字符串使得 $j$ 每次只移动一步,然后一直退回到 $0$。
而且之后的一道题 [CEOI2011]Matching - 洛谷 也充分地说明了,即使 $j$ 指针每次只向后挪动一位,复杂度仍然是 $O(n)$。
我们发现 $j$ 指针每次是从 $\pi[i-1]$ 开始,可能会往左退,然后如果匹配了,会向右 $+1$。实际上是接着上一次 $j$ 指针的位置继续移动。
于是可以发现 $j$ 只会向右移动 $n$ 次,而向左移动时 $j\ge0$,因此向左移动也不会超过 $n$ 次。复杂度为 $O(n)$。