学习笔记 - 快速沃尔什变换FWT

FWT之前学过，但是不太扎实，复习FST的时候看到了……发现已经忘了

所以重新学了一遍 QwQ

---

# 什么是FWT

和FFT一样，是一种数列变换。

我们知道 FFT 求解的是多项式乘法：$F_i=\sum\limits_{p+q=i}G_pH_q$，换句话说就是卷积。但是卷积并不局限于简单的多项式乘法……比如下面这个也是卷积：

$$F_i=\sum_{p\oplus q=i}G_pH_q$$

于是对于 FFT 来说，式子中的 $\oplus$ 是整数加法。

而对于 FWT，它解决的是 $\oplus=\text{XOR,OR,AND}$（按位异或、按位或、按位与）中的任意一种。和 FFT 一样，FWT 能将原本 $O(n^2)$ 计算的卷积优化到 $O(n\log n)$。

我们把一个数列 $A$ 经过 FWT 变换得到的序列记作 $FWT[A]$，以达到 $FWT[F]_i=FWT[G]_i\times FWT[H]_i$（整数乘法）的目的。

---

# 或卷积 FWTOR

Note. 方便起见，下文中 |,\&,^ 分别代指或、与和异或。

- 理论推导

FWT 用到的是位运算的一些性质——若 $a|c=c$ 且 $b|c=c$，则 $(a|b)|c=c$；可以从集合意义理解：$a$ 是 $c$ 的子集且 $b$ 是 $c$ 的子集，那么 $a,b$ 的并集也是 $c$ 的子集。

于是我们定义：

$$FWT[A]_i=\sum_{j|i=i}A_j$$

我们是否已经达到了 $FWT[F]_i=FWT[G]_i\times FWT[H]_i$ 的目的了呢？可以验算一下：

$$\begin{split} FWT[F]_i&=FWT[G]_i\times FWT[H]_i\\ &=\sum_{j|i=i}G_j\times\sum_{k|i=i} H_k\\ &=\sum_{j|i=i}\sum_{k|i=i} G_jH_k\\ &=\sum_{(j|k)|i=i}G_jH_k\\ &=\sum_{x|i=i}\sum_{j|k=x}G_jH_k\\ &=\sum_{x|i=i}F_x \end{split}$$

与 $FWT[F]_i$ 的定义式是一样的，这就是或变换。

- 代码实现

Note. 假设 $A$ 是一个有 $2^n$ 项的多项式。

用分组计算的方法——定义临时变量 $P[0\sim n-1]$，$P[i]$ 是一个多项式，$P[i]_j$ 是 $A_x$ 的和，其中 $x$ 满足高位开始的 $i$ 个位置（二进制下）和 $j$ 相同，且记 $x$ 剩下的位置为 $x’$，$j’$ 同理，则 $x’|j’=j’$。

于是我们发现 $P[n-1]=A$，$P[0]=FWT[A]$。

而 $P[i]$ 是可以由 $P[i-1]$ 推过来的——

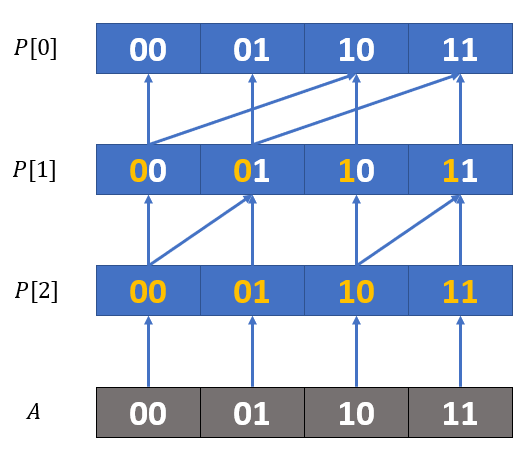
上图的箭头表示了某一个值是由哪些值加起来得到的，比如 $P[1]_{01}$ 就是由 $P[2]_{00}+P[2]_{01}$ 得到的。逆变换也可以通过这张图得到，比如 $P[2]_{11}=P[1]_{11}-P[1]_{10}$。

于是可以用类似于 FFT 的方法实现，详见文末代码。

---

# 与卷积 FWTAND

这里用到了按位与的性质：若 $b\&a=a$ 且 $c\&a=a$，则 $(b\&c)\&a=a$。

同理构造 $FWT[A]_i=\sum\limits_{j\&i=i}A_j$。

---

# 异或卷积 FWTXOR

相对复杂。定义运算 $i\otimes j$ 表示二进制数 $(i\& j)$ 中 $1$ 的个数的奇偶性，则有性质 $(a\otimes b)\text^(a\otimes c)=a\otimes(b\text^ c)$。

根据这一点，我们构造：

$$FWT[A]_i=\sum_{i\otimes j=0}A_j-\sum_{i\otimes j=1}A_j$$

同样，我们来验证一下这样构造是否达到目的：

$$\begin{split} FWT[F]_i&=FWT[G]_i\times FWT[H]_i\\ &=\left(\sum_{i\otimes j=0}G_j-\sum_{i\otimes j=1}G_j\right)\left(\sum_{i\otimes j=0}H_j-\sum_{i\otimes j=1}H_j\right)\\ &=\sum_{i\otimes j=0}G_j\sum_{i\otimes k=0}H_k-\sum_{i\otimes j=1}G_j\sum_{i\otimes k=0}H_k-\sum_{i\otimes j=0}G_j\sum_{i\otimes k=1}H_k+\sum_{i\otimes j=1}G_j\sum_{i\otimes k=1}H_k\\ &=\sum_{i\otimes(j\text^k)=0}G_jH_k-\sum_{i\otimes(j\text^k)=1}G_jH_k \end{split}$$

说明这样构造是成立的。

仍然采用分组计算的方法，而画出来的图就更加复杂了：

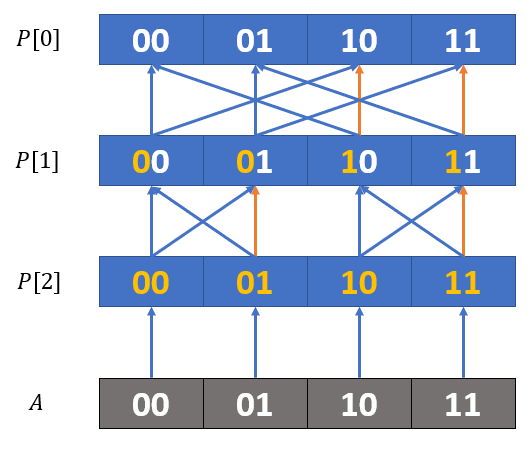
蓝色边表示“正向”，即箭头方向的值加上箭尾的值；橙色边表示反向，即减去箭尾的值。因为当 $1\&1=1$ 时，会新增一个 $1$，则奇偶改变。

---

# 源代码

namespace FWT{
    const int MOD=998244353;
    inline int FAdd(const int &a,const int &b){return a+b>=MOD? a+b-MOD:a+b;}
    inline int FSub(const int &a,const int &b){return a-b<0? a-b+MOD:a-b;}
    inline int FMul(const int &a,const int &b){return 1ll*a*b%MOD;}
    inline int FPow(int a,int b){int ret=1;while(b){if(b&1)ret=FMul(ret,a);a=FMul(a,a);b>>=1;}return ret;}
    const int INV2=FPow(2,MOD-2);
    void FWTOR(int *ary,const int &len,const int &typ){
        for(int L=2,T=1;L<=len;L<<=1,T<<=1)
            for(int i=0;i<len;i+=L)
                for(int j=i;j<i+T;j++)
                    if(typ==1) ary[j+T]=FAdd(ary[j+T],ary[j]);
                    else ary[j+T]=FSub(ary[j+T],ary[j]);
    }
    void FWTAND(int *ary,const int &len,const int &typ){
        for(int L=2,T=1;L<=len;L<<=1,T<<=1)
            for(int i=0;i<len;i+=L)
                for(int j=i;j<i+T;j++)
                    if(typ==1) ary[j]=FAdd(ary[j],ary[j+T]);
                    else ary[j]=FSub(ary[j],ary[j+T]);
    }
    void FWTXOR(int *ary,const int &len,const int &typ){
        for(int L=2,T=1;L<=len;L<<=1,T<<=1)
            for(int i=0;i<len;i+=L)
                for(int j=i;j<i+T;j++){
                    int Aj=ary[j];
                    ary[j]=FAdd(Aj,ary[j+T]);
                    ary[j+T]=FSub(Aj,ary[j+T]);
                    if(typ==-1)
                        ary[j]=FMul(ary[j],INV2),ary[j+T]=FMul(ary[j+T],INV2);
                }
    }
}

---

THE END

Thanks for reading!

$$\begin{split} “\ &你走吧\ 趁着落日长天\\ &你走吧\ 此去山遥路远\\ &愿夜里秋风温暖\ 街头不寒\\ &你走吧\ 趁着天色未暗\\ &你走吧\ 深知道阻且难\\ &我献上明月一盏\ 照满河山”\\ \text{—}&\text{—《山遥路远》By ChiliChill} \end{split}$$