学习笔记 - 回文自动机PAM | Lucky_Glass's Blog

以心为名，名为爱惜

0%

学习笔记 - 回文自动机PAM

发表于 更新于 分类于 Valine：

一类能够接受一个主串内的所有回文子串的自动机~

# 概念

回文自动机PAM非常类似于后缀自动机SAM，或许是借鉴了SAM的灵感。

具体地说，PAM的每个节点代表一个回文串，并且节点（除了起始节点）与主串中的所有回文子串一一对应，也具有两种边：

  1. 转移边 next[c]，指向将当前节点代表的回文串的两端加上字符 c得到的回文串的节点。
  2. 后缀边 link，指向当前节点代表的回文串的最长的回文真后缀的节点。

所有转移边构成一个 DAG，所有后缀边构成一棵树。

但是与SAM不同，PAM有两个起始节点 0 和 -1。因为回文串根据长度的奇偶可以分为两类，那么就相应地——在 0 的两端加字符相当于是一个偶回文串，而在 -1 两端加字符相当于得到一个奇回文串。

除此之外，每个节点还维护了信息 $len$，即对应的回文串的长度。

# 构造

给定主串 $S$，要求构造 $S$ 的PAM。

这里比SAM要简单好多

初始化，不难理解：0 的 $len$ 为 $0$，-1 的 $len$ 为 $-1$。然后 0 的 link 指向 -1，可以这样理解：0 代表“偶空串”，由两个空字符组成；-1 代表“奇空串”，由一个空字符组成。

仍然使用增量法，从上一个位置结尾的最长的回文串开始，向两边扩展。设当前要插入位置为 $i$，当前位置的字符为 $c$，上一个位置 $i-1$ 的对应节点为 $las$，初始情况 $las=-1$。

  1. 如果 $S_{i}=S_{i-len[las]-1}$，也就是 $i-len[las]-1$ 到 $i$ 是一个回文串，则无需操作；

  2. 如果 $S_i\not= S_{i-len[las]-1}$，则将 $las$ 移动到 $link[las]$ 后再检验是否形成回文，即移动到一个更小的回文串再判断；最后一定会找到满足条件的 $las$，因为一个字符本身就是一个回文串，此时 $las$ 会跳回 $-1$。

  3. 如果 $next[las][c]$ 不为空，表示这个回文串已经出现过了，则 $las$ 移动到 $next[las][c]$；

  4. 如果 $next[las][c]$ 是空，表示这个回文串是第一次出现，则新建节点 $cur$；

    $len[cur]=len[las]+2$，即在原回文串的两端加上字符 $c$；

    然后求 $link[cur]$，从 $link[las]$ 开始沿着 $link$ 边向上跳，直到找到回文后缀为止；如果找到了回文后缀，则 $link[cur]$ 指向该位置；如果没有（可能 $cur$ 就是一个字符构成的回文），则 $link[cur]$ 指向 $0$；

# 时空复杂度

PAM 的优越的复杂度基于“一个长度为 $n$ 的字符串最多有 $n$ 个本质不同的回文子串”这个事实。

证明比较简单，只需要证明向原字符串的末尾添加一个字符，最多只会增加一个本质不同的回文子串。

png1

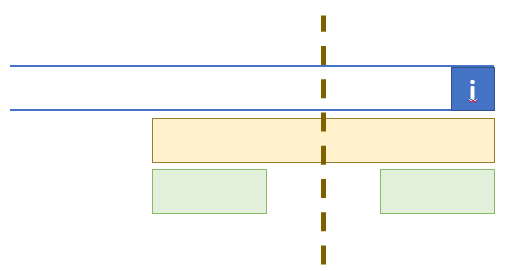
在原字符串末尾加上位置 $i$，则除了以 $i$ 结尾的最长的回文子串（图中黄色片段）可能是第一次出现，其他以 $i$ 结尾的回文子串（比如绿色片段）一定出现过，因为可以对称过去（以黄色片段的中点对称）找到一个一样的字符串。

那么，PAM 的点数就只有 $n+2$ 个（两个起始点），空间复杂度 $O(n)$，link树的深度达到 $O(n)$。

增量法构造的时间复杂度也是 $O(n)$，分析增量法中一直在移动的 $las$ 指针：

  1. $las$ 只会沿着 $next$ 边走 $n$ 次，每次 $len[las]$ 增加 $1$；
  2. $las$ 沿着 $link$ 边走，$len[las]$ 严格减小。

那么由于 $len[las]\ge-1$，则沿着 $link$ 边走的次数为 $O(n)$，则时间复杂度也为 $O(n)$。

# 局限

虽然 PAM 非常优秀，但是它还是不能完全顶替 Manachar：

  1. PAM 的空间开销巨大，因为字符集大小一般是 26，光是 next 数组就要开 $26\times n$ 这么多；除非时间换空间，用 hash 储存图（因为 next 边的数量只有 $O(n)$）
  2. PAM 求的是以一个位置结尾的回文串，而 Manachar 求的是以一个位置为中点的回文串，有些题用 PAM 就比较麻烦

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
char str[N];
struct PAMAUTO{
    int nxt[N][26],lnk[N],len[N],ncnt;
    void Init(){
        ncnt=2;
        len[1]=-1,lnk[1]=1; //当然实际实现不可能下标用 0 和 -1
        len[2]=0,lnk[2]=1;
    }
    int Match(int u,const int &pos){ //沿着link边跳，直到找到回文后缀
        while(str[pos]!=str[pos-len[u]-1]) u=lnk[u];
        return u;
    }
    void Build(const int &L,int *res){
        Init();
        for(int i=0,las=1;i<L;i++){
            int c=str[i]-'0';
            las=Match(las,i);
            if(!nxt[las][c]){ //第一次出现
                int cur=++ncnt,tmp;
                len[cur]=len[las]+2;
                tmp=Match(lnk[las],i);
                if(nxt[tmp][c]) lnk[cur]=nxt[tmp][c];
                else lnk[cur]=2;
                nxt[las][c]=cur,las=cur;
            }
            else las=nxt[las][c];
            res[i]=len[las];
        }
    }
};

THE END

Thanks for reading!