OI - Jumping on a Cactus(HDU) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI - Jumping on a Cactus(HDU)

发表于 分类于 Valine：

这道题放在T2好像不太合适……

# 题面

点击展开/折叠 题面

给定一个点数为 $n$ 的仙人掌 $G$ 以及起点 $S$，保证仙人掌没有奇环，设 $d_i$ 表示 $i$ 与 $S$ 的最短距离（边的长度均为 $1$）。

你需要计算有多少个 $1\sim n$ 的排列 $P$，使得对于任意 $(i,j)$，若 $d_i< d_j$，则 $p_i< p_j$。

$1\le n\le5000$（虽然勉勉强强可以开到 $10^4$）

# 解析

发现 $O(n^2)$ 可过，于是有两种做法~

- 正向DP

跑一遍最短路（BFS）过后可以给每条边定向得到一个有向图，于是称一个点 $u$ 经过有向边能到达的点为 $u$ 的后继。按照题目的意思，$u$ 的后继 $v$ 一定有 $p_u< p_v$。

先考虑简单的情况——一棵树，则 $u$ 的后继就是 $u$ 的子树。设 $g_u$ 表示 $u$ 及 $u$ 的子树内的合法的 $P$ 的方案数（子问题）。

子树 $v$ 合并到 $u$ 上时，要保证 $u,v$ 原来的 $P_u,P_v$ 的顺序，而 $u,v$ 之间的顺序是没有要求的，于是可以在合并后的 siz[u]+siz[v] 个位置中挑选出 siz[v] 个位置分配给 $P_v$，即

再把环给加上。

定义一个环上 $d_i$ 最小的点 $i$ 为环的“顶点”，因为是仙人掌，所以每个环只有一个顶点；又因为只存在偶环，所以每个环上只有一个 $d_i$ 最大的点，称为环的“中点”。

环的顶点一定是 $p$ 最小的，因此可以删掉顶点，然后环就有了两个端点，则只需要决策两端点哪一个 $p$ 更小。

定义 $f_{i,j}$ 表示当前已经决策了 $i,j$ 及其后继的 $p$ 的合法方案数。如果让 $i$ 的 $p$ 更小（让 $j$ 的 $p$ 更小是差不多的），如图：

png1

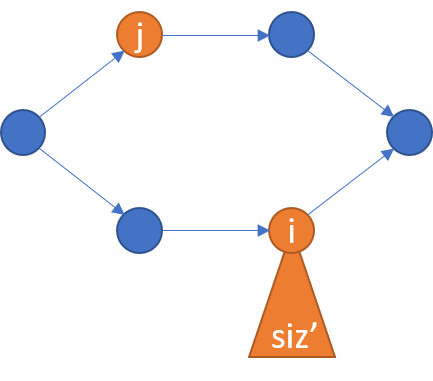
此时 $g_i$ 已经计算出了 $i$ 以及图中 $siz’$ 的 $P$ 的方案数。设 $i,j$ 及 $i,j$ 后继的数量共有 $tot$ 个，则需要从 $tot$ 个位置中：先把最小的 $p$ 留给 $i$，然后保持 $g_i$ 对应的排列的顺序，只需要从剩下的 $tot-1$ 个位置中选出 $siz’$ 个。即 $\binom{tot-1}{siz’}f_{i+1,j}g_i$

于是总的转移式就是：

最后把整个环的 $f$ 转移到其顶点 $u$ 的 $g_u$ 上就可以继续转移了。

实现的时候建圆方树要方便一些，而且可以把不在环上的边看成一个只有两个点的环，那么在圆方树上一定是圆方交替，就可以少些特判。

- 反向DP

即从 $n!$ 全排列中删去不合法的。

从更为简单的链开始考虑，设 $i$ 之后的点的 $p$ 已经决策好了

png2

则此时在全排列中，$p_1< p_2< p_3$，那么 $p_i$ 在不考虑 $i$ 的合法性的全排列中的取值将有 $p_i< p_1$、$p_1< p_i< p_2$、$p_2< p_i< p_3$、$p_3< p_i$ 这 $4$ 类，且每一类对应的排列数相同。

但是只有 $p_i< p_1$ 这一类是合法的，于是总排列数除以4得到合法的排列数。

不难发现，在决策 $i$ 时，会有 siz[i] 种类型，而只有一种类型是合法的，因此总排列数除以 $siz_i$。于是链的方案数只有 $\frac{n!}{\prod siz_i}=1$

实际上链的结论可以扩展到树上，在 $u$ 的子树内的排列 $P_u$ 中，$p_u$ 的取值也有 $siz_u$ 类，除以 $siz_u$ 同理。即树的结论是 $\frac{n!}{\prod siz_i}$。

然而这个结论不能直接用在仙人掌上，就是因为有环。不过可以发现仙人掌上的环的贡献（从全排列中除去不合法的贡献）是互相独立的，于是考虑对每个环进行DP。

$f_{i,j}$ 表示环内已经决策 $i,j$ 及其后继的 $p$ 的大小关系，除去的不合法的方案数是多少（一个分数）。

（仍然沿用“正向DP”中对环上的点的一些称谓）

中点 $mid$ 的 $p$ 一定小于其后继节点（不在环上），则 $f_{mid,mid}=\frac1{siz_{mid}}$。若使 $p_i< p_j$，设 $i,j$ 的后继共有 $tot$ 个，则在 $tot$ 类 $p_i$ 的取值中，只有 $p_i$ 最小的一种合法，则 $f_{i,j}=\frac{f_{i+1,j}}{tot}$，其中 $tot=siz_i+siz_j-siz_{mid}$；实际上 $p_j< p_i$ 的情况是完全一样的，即：

环的顶点的贡献直接是 $\frac1{siz}$，因为它的 $p$ 一定是最小的。

另外还有一些点不在环上，和顶点同理，贡献是 $\frac1{siz}$。

# 源代码

- 正向DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
/*Lucky_Glass*/
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

inline int Read(){
	register int r=0,c=getchar();
	while(c<'0' || '9'<c) c=getchar();
	while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
	return r;
}

const int N=1e4+10,M=N<<1,MOD=998244353;
#define ci const int &
inline int Add(ci a,ci b){return a+b>=MOD? a+b-MOD:a+b;}
inline int Sub(ci a,ci b){return a-b<0? a-b+MOD:a-b;}
inline int Mul(ci a,ci b){return 1ll*a*b%MOD;}
inline int Pow(int a,int b){int r=1;while(b){if(b&1)r=Mul(r,a);a=Mul(a,a),b>>=1;}return r;}

struct GRAPH{
	int head[N<<1],to[M<<1],nxt[M<<1],ncnt;
	void AddEdge(ci u,ci v){
		int p=++ncnt,q=++ncnt;
		to[p]=v,nxt[p]=head[u],head[u]=p;
		to[q]=u,nxt[q]=head[v],head[v]=q;
	}
	inline int operator [](ci u){return head[u];}
}Gr,Ne;

int n,m,s,ndfn,nscc,nstk;
int dfn[N],low[N],stk[N],siz[N<<1],sz[N];
int fac[N],ifac[N];
int g[N<<1],f[N][N];
vector<int> cir[N];

void Tarjan(ci u){
	dfn[u]=low[u]=++ndfn;
	stk[++nstk]=u;
	for(int it=Gr[u];it;it=Gr.nxt[it]){
		int v=Gr.to[it];
		if(dfn[v]) low[u]=min(low[u],dfn[v]);
		else{
			Tarjan(v),low[u]=min(low[u],low[v]);
			if(low[v]==dfn[u]){
				nscc++;
				Ne.AddEdge(nscc+n,u);
				for(int tmp=-1;tmp!=v;nstk--){
					Ne.AddEdge(nscc+n,tmp=stk[nstk]);
					cir[nscc].push_back(tmp);
				}
			}
		}
	}
}
inline int Comb(ci a,ci b){return Mul(fac[b],Mul(ifac[a],ifac[b-a]));}
void DFS(ci u,ci fa){
	if(u<=n){
		g[u]=1;
		for(int it=Ne[u];it;it=Ne.nxt[it]){
			int v=Ne.to[it];
			if(v==fa) continue;
			DFS(v,u);
			siz[u]+=siz[v];
			g[u]=Mul(g[u],Mul(g[v],Comb(siz[v],siz[u])));
		}
		siz[u]++;
	}
	else{
		for(int it=Ne[u];it;it=Ne.nxt[it]){
			int v=Ne.to[it];
			if(v==fa) continue;
			DFS(v,u),siz[u]+=siz[v];
		}
		vector<int> &cur=cir[u-n];
		int ns=cur.size(),mid=ns/2,szmid=siz[cur[mid]];
		sz[mid]=szmid;
		for(int i=mid-1;~i;i--) sz[i]=sz[i+1]+siz[cur[i]];
		for(int i=mid+1;i<ns;i++) sz[i]=sz[i-1]+siz[cur[i]];
		for(int i=mid;~i;i--)
			for(int j=mid;j<ns;j++){
				if(i==j) f[i][j]=g[cur[mid]];
				else{
					f[i][j]=0;
					int key=sz[i]+sz[j]-szmid;
					if(i<mid) f[i][j]=Add(f[i][j],Mul(Mul(f[i+1][j],g[cur[i]]),Comb(siz[cur[i]]-1,key-1)));
					if(j>mid) f[i][j]=Add(f[i][j],Mul(Mul(f[i][j-1],g[cur[j]]),Comb(siz[cur[j]]-1,key-1)));
				}
			}
		g[u]=f[0][ns-1];
	}
}
int main(){
	freopen("abgfriend.in","r",stdin);
	freopen("abgfriend.out","w",stdout);
	n=Read(),m=Read(),s=Read();
	for(int i=1;i<=m;i++) Gr.AddEdge(Read(),Read());
	fac[0]=1;
	for(int i=1;i<=n;i++) fac[i]=Mul(fac[i-1],i);
	ifac[n]=Pow(fac[n],MOD-2);
	for(int i=n-1;i>=0;i--) ifac[i]=Mul(ifac[i+1],i+1);
	Tarjan(s),DFS(s,0);
	printf("%d\n",g[s]);
	return 0;
}

- 反向DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
/*Lucky_Glass*/
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

inline int Read(){
	register int r=0,c=getchar();
	while(c<'0' || '9'<c) c=getchar();
	while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
	return r;
}

const int N=1e4+10,M=N<<1,MOD=998244353;
#define ci const int &
inline int Add(ci a,ci b){return a+b>=MOD? a+b-MOD:a+b;}
inline int Sub(ci a,ci b){return a-b<0? a-b+MOD:a-b;}
inline int Mul(ci a,ci b){return 1ll*a*b%MOD;}
inline int Pow(int a,int b){int r=1;while(b){if(b&1)r=Mul(a,r);a=Mul(a,a),b>>=1;}return r;}

struct GRAPH{
	int head[N],to[M<<1],nxt[M<<1],ncnt;
	GRAPH(){ncnt=1;}
	void AddEdge(ci u,ci v){
		int p=++ncnt,q=++ncnt;
		to[p]=v,nxt[p]=head[u],head[u]=p;
		to[q]=u,nxt[q]=head[v],head[v]=q;
	}
	inline int operator [](ci u){return head[u];}
}Gr;

int n,m,s;
int siz[N],dis[N],fa[N],inv[N],A[N],B[N],f[N][N];
bool ban[M],oncir[N];
vector< pair<int,int> > cir;

void BFS(){
	queue<int> que;
	que.push(s);
	dis[s]=1;
	while(!que.empty()){
		int u=que.front();que.pop();
		for(int it=Gr[u];it;it=Gr.nxt[it]){
			int v=Gr.to[it];
			if(dis[v]){
				if(dis[v]>dis[u]){
					ban[it>>1]=true;
					cir.push_back(make_pair(u,v));
				}
				continue;
			}
			fa[v]=u;
			dis[v]=dis[u]+1;
			que.push(v);
		}
	}
}
void DFS(ci u){
	siz[u]=1;
	for(int it=Gr[u];it;it=Gr.nxt[it]){
		int v=Gr.to[it];
		if(ban[it>>1] || v==fa[u]) continue;
		DFS(v),siz[u]+=siz[v];
	}
}
int main(){
	freopen("abgfriend.in","r",stdin);
	freopen("abgfriend.out","w",stdout);
	int ans=1;
	n=Read(),m=Read(),s=Read();
	for(int i=1;i<=m;i++) Gr.AddEdge(Read(),Read());
	for(int i=1;i<=n;i++) ans=Mul(ans,i),inv[i]=Pow(i,MOD-2);
	BFS(),DFS(s);
	//for(int i=1;i<=n;i++) printf("%d: %d\n",i,siz[i]);
	for(int i=0,I=cir.size();i<I;i++){
		int u=cir[i].first,v=cir[i].second,nA=0,nB=0,low=v;
		oncir[v]=true;
		v=fa[v];
		while(u!=v){
			oncir[u]=oncir[v]=true;
			A[++nA]=u,B[++nB]=v;
			u=fa[u],v=fa[v];
		}
		for(int p=0;p<=nA;p++)
			for(int q=0;q<=nB;q++)
				if(p && q) f[p][q]=Mul(Add(f[p-1][q],f[p][q-1]),inv[siz[A[p]]+siz[B[q]]]);
				else if(p) f[p][q]=Mul(f[p-1][q],inv[siz[A[p]]+siz[low]]);
				else if(q) f[p][q]=Mul(f[p][q-1],inv[siz[B[q]]]);
				else f[p][q]=inv[siz[low]];
		ans=Mul(ans,f[nA][nB]);
	}
	for(int i=1;i<=n;i++)
		if(!oncir[i])
			ans=Mul(ans,inv[siz[i]]);
	printf("%d\n",ans);
	return 0;
}

THE END

Thanks for reading!

> Linked 不可道-网易云