游记&OI - 广州纪中游记 Day13 & Day14 | Lucky_Glass's Blog

以心为名，名为爱惜

0%

游记&OI - 广州纪中游记 Day13 & Day14

发表于 更新于 分类于 Valine：

<题面链接> 提取码：7puf

Part1. 游记

= Day13

还有两天就要结束了，我好开心啊 (*^▽^*)

听说今天要考数学……数学……你考啊，我又不怕（？？？蜜汁自信）。然后一看题目，哟，你还真敢考数学。

首先题目标题有明显暗示：

T1. Count

字面上理解就是数数嘛……乍一看真的就全是数数题（QwQ）

T2. 普及组

连普及组都考成这样了，你还是退役吧……

T3. 提高组

你说去年普及组比提高组难？或许打提高组分数会高一些？你试一试……

ヽ(°◇° )ノ

不过题难了就会导致平均分极低……大概 40~50……竟然 65 分还挤到前面来了 awa。

= Day14

还有一天就结束了我真的好开心啊（上蹿下跳）

另外，这篇游记就是在当日晚上写的诶！！！终于有一天的游记是在当天写的了！！

所以说，我可能记起来的事情就比之前多好多了~

今天讲课，图论专题。

上午有一点嫌弃太水了，虽然有一个最小生成树的算法我没有听说过，但是感觉就为了这一个去听完整堂课有一点浪费时间，于是 咕咕咕。

然后下午和 tly 神犇去听网络流，其实我是奔着最小割、费用流、有上下界的网络流去的。

tly 神了！带着个笔记本去上课，边上课边打多校。这边讲课出一道题目他就看一下，然后基本上就切掉了 %%% 到讲台上去讲了两道题（666666），然后我……还好在 tly 的提示下想出来了一个最小割的裸题，上去讲了一发 em…… 上台的时候画图演示，看得出来的手抖 ⌇●﹏●⌇，就不像 taotao 这么自然从容……最后多校因为 tly 的电脑没电了（23333），然后就锅了。

顺带吐槽一波，这次的讲师又是上次那个讲数据结构讲得不是特别好的同学……不过这次讲课质量很有起色呢！

晚上依然没去，跟几个同学又拿着一副勉强能用的乒乓球拍去运动了一下，出了一身汗，希望不要感冒 TAT

明天因为是最后一天了嘛，但是除了 Day9 去珠海领略了一下广州风光，我们还没有去过别的什么广州著名景点呢…… 然后家长就给我们安排去孙中山故居去参观（咕了午觉去参观……）。

然后透露一下行程，后天一早就要走了，6:40 就要从学校出发（好早啊），而且 6:00 就要把床铺收好，也就是说大概 5:00 起来比较合适，多设几个闹钟应该起得来 2333。至于吃饭的事情……早饭吃零食（来这里第一天就发下来的零食干粮现在还剩了一堆，至少我是这样的），午饭听说高铁上很贵，可能得吃方便面了 TAT（其实这两天方便面吃的也不少）

ah~ 其实今天的收获还是挺多的~ 写游记只是这么多重要的事情中的一个，于是，下面进入正题（众所周知）

Part2. Solution

真的全是数数题啊！！！

不过知识点还是很全的（放心，没有数论）

T1. Count(count)

[Experience]

看到这题的时候就开始懵推式子，最后推出来一个其实跟正解已经很接近了的式子，但是莫名其妙我想到了中国剩余定理（可能因为之前考过，印象比较深刻）……

然后就偏离正解了。

[Solution]

= 第一步

我们令 $b_i=a_i\bmod m$，$A=\sum_{i=1}^kb_i$ ，然后令 $a_i=t_im+b_i$ （$t_i\ge0$ 且 $1\leq b_i\leq m-1$）

Q：$t_i$ 和 $b_i$ 的范围怎么确定的？

A：由于 $b_i$ 是 $a_i$ 对 $m$ 取模的结果，所以 $b_i\leq m-1$，而又因为 $a_i$ 不是 $m$ 的倍数，则 $b_i\ge 1$，所以 $1\leq b_i\leq m-1$；

    而因为 $b_i\leq a_i$，所以 $t_i=\frac{a_i-b_i}{m}\ge0$ 。

这样对于每个 $a_i$ ，显然 $t_i$ 与 $b_i$ 的取值是互不影响的，我们只要分别确定出 $t_i$ 的方案数以及 $b_i$ 的方案数，乘法原理相乘一下即可得到 $a_i$ 的方案数。

= 分配 $t_i$

可以得到：

又因为 $\sum_{i=1}^ka_i=n$，则有：

根据 $A$ 的定义式可知 $m|n-A$ ，即：

其中 $t_i\ge0$，所以 $t_i$ 的不同的方案数相当于“把 $\frac{n-A}m$ 个无区别球，放进 $k$ 个有区别的箱子里，允许空箱”，组合数一下就是 $C_{\frac{n-A}m+k-1}^{k-1}$ 。

= 分配 $b_i$

因为 $A=\sum_{i=1}^kb_i$ 且 $1\leq b_i\leq m-1$，所以 $k\leq A\leq k(m-1)$ ；

又因为 $\sum_{i=1}^ka_i=m\sum_{i=1}^kt_i+A$ 且 $\sum_{i=1}^ka_i=n$；则有：

换个式子：

由于可以知道在 $[k,k(m-1)]$ 中与 $n$ 模 $m$ 同余的数不超过 $k$ 个，所以我们可以考虑枚举 $A$ 。

枚举出 $A$ 后，我们就要把 $A$ 分配给 $b_i$ 了，那么就相当于 “把 $A$ 个无区别球放进 $k$ 个盒子，不允许空盒，且每个盒子中球的个数不超过 $(m-1)$”。emm……好像就是多了一个条件：盒子中球的个数不超过 $(m-1)$ 。

于是我们考虑 容斥，定义函数 $F(i)$ 表示把 $i$ 个无区别球分配给 $k$ 个盒子，无空盒的方案数，这就非常简单了，不难得到 $F(i)=C_{i-1}^{k-1}$ 。关于容斥，式子大概就是：

{至少有0个盒子中球超过 m-1 个} - {至少有1个盒子中球超过 m-1 个} + {至少有2个盒子中球超过 m-1 个} … + (-1)^k * {至少有k个盒子中球超过 m-1 个}

也就是：

$F(A)\times C_k^0-F(A-(m-1))\times C_{k}^1+F(A-2(m-1))\times C_k^2…+(-1)^kF(A-k(m-1)\times C_k^k)$；

换个简单的式子：

其中 $(-1)^i$ 是容斥系数，$C_k^i$ 是从 $k$ 个盒子中选出 $i$ 个盒子，令它们中的球超过 m-1 个，那么对应的，有 $i(m-1)$ 个球已经固定分给 $i$ 个盒子了（为了使它们的球的个数超过 m-1），剩余 $A-i(m-1)$ 个球就可以随机分给 $k$ 个盒子了。

然后预处理一下组合数就好啦？

对，是要处理组合数，但不是单单预处理这么简单（坑了我好久，就留给 reader 们想了）……这里提醒各位：一定要先枚举 A，再进行容斥！不然时间复杂度会出问题！

[Source]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const ll MOD=998244353ll,K=2000,M=5000;

ll n,m,k;
ll inv[K+3];
ll fac[K*M+3],invfac[K*M+3];

ll fucC(ll cura,ll curb){
	if(curb>=K*M){ //因为组合数的参数太大，无法预处理
		if(cura>curb) return 0;
		ll ret=1;
		for(ll i=1;i<=cura;i++)
			ret=ret*inv[i]%MOD*((curb-cura+i)%MOD)%MOD;
		return ret;
	}
	if(cura>curb) return 0;
	//这里可以预处理了
	return fac[curb]*invfac[cura]%MOD*invfac[curb-cura]%MOD;
}
ll QPow(ll cura,ll curb){
	ll ret=1;
	while(curb){
		if(curb&1) ret=ret*cura%MOD;
		cura=cura*cura%MOD;
		curb>>=1;
	}
	return ret;
}
int main(){
	fac[0]=1;
	for(int i=1;i<K*M;i++) fac[i]=fac[i-1]*i%MOD;
	invfac[K*M-1]=QPow(fac[K*M-1],MOD-2);
	for(int i=K*M-2;i>=0;i--) invfac[i]=invfac[i+1]*(i+1)%MOD;
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	scanf("%lld%lld%lld",&n,&m,&k);
	for(int i=1;i<=K;i++) inv[i]=QPow(i,MOD-2);
	ll ans=0;
	for(ll A=n%m;A<=k*(m-1);A+=m){
		ll tmp=1,res=0;
		for(ll y=0;y<=k && A-y*(m-1)-1>=k-1;y++){
			res=(res+tmp*fucC(k-1,A-y*(m-1)-1)%MOD*fucC(y,k)%MOD+MOD)%MOD;
			tmp*=-1;
		}
		ans=(ans+res*fucC(k-1,k+(n-A)/m-1)%MOD)%MOD;
	}
	printf("%lld\n",ans);
	return 0;
}

T2. 普及组(pj)

[Experience]

这道题考场上完全没有思路，甚至没有想到这竟然是个 DP……

然后先推了一下式子，没推出来，就开始打表，好不容易找出来 $x=1$ 的规律。

[Solution]

首先考虑方格图里的正负，因为 $x$ 是正数，所以最后每一行每一列中都有偶数个负数，方案数为 $2^{(n-1)^2}$

然后考虑把 $x$ 分解质因数——发现 $x$ 的相同质因数的个数最大为 $2$ 。我们发现我们可以把每个质因子分别求出一个矩阵，然后方案数乘起来。

把质因子分成以下两类：

  1. 该质因子的个数为 $1$：方案数为 $n!$ ，不给解释……
  2. 该质因子的个数为 $2$：这样就需要 DP 了，可以将问题转换为在 $n\times n$ 的方格图里填 $0,1$ 或 $2$，使得每一行、每一列的和都是 $2$。

于是考虑 DP，F[i] 表示在最后一列填上两个 1，G[i] 表示最后一列填上一个 2，考虑转移：

首先 G[i] ，因为最后一列填了一个 2，所以 2 所在的那一行、那一列都不会再填数字了，所以可以把 2 所在行和列删去，变为 i-1 行 i-1 列的方格图，也就是说：G[i]=F[i-1]+G[i-1]；

然后 F[i]，我讲不清楚TAT，反正就是 F[i]=2F[i-1]+G[i-1] 。（知道的 reader 们可以邮箱中爆踩我）

然后打表算一下对于每个 $x$ ，需要乘多少个质因子个数为 1 的方案数、多少个质因子个数为 2 的方案数，然后预处理+输出答案即可。

[Source]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=5e6;
const ll MOD=998244353;

ll F[N+3],G[N+3],ans[N+3],fac[N+3];

ll x;
int T;

void GetAns(int cnt1,int cnt2){
	for(int i=1;i<=N;i++){
		ans[i]=1;
		for(int j=1;j<=cnt1;j++)
			ans[i]=int(1ll*ans[i]*fac[i]%MOD);
		for(int j=1;j<=cnt2;j++)
			ans[i]=int(1ll*ans[i]*(G[i]+F[i])%MOD);
	}
}
ll QPow(ll cura,ll curb){
	ll ret=1;
	while(curb){
		if(curb&1) ret=ret*cura%MOD;
		cura=cura*cura%MOD;
		curb>>=1;
	}
	return ret;
}
int main(){
	freopen("pj.in","r",stdin);
	freopen("pj.out","w",stdout);
	fac[0]=1;
	for(int i=1;i<=N;i++)
		fac[i]=fac[i-1]*i%MOD;
	G[1]=1;
	for(int i=2;i<=N;i++){
		if(i&1) F[i]=1ll*(i-1)/2*i%MOD*(2*F[i-1]+G[i-1])%MOD;
		else F[i]=1ll*i/2*(i-1)%MOD*(2*F[i-1]+G[i-1])%MOD;
		G[i]=(F[i-1]+G[i-1])*i%MOD;
	}
	scanf("%lld%d",&x,&T);
	switch(x){
		case 3ll : GetAns(1,0);break;
		case 12ll: GetAns(1,1);break;
		case 30ll: GetAns(3,0);break;
		case 1ll : GetAns(0,0);break;
		case 147203573614806055ll : GetAns(5,0);break;
		case 371216956151518818ll : GetAns(6,0);break;
		case 834586893457709917ll : GetAns(4,0);break;
		case 1147387575560213988ll: GetAns(3,7);break;
		case 608358758975305374ll : GetAns(3,3);break;
		case 710701671428663075ll : GetAns(2,3);break;
		case 714115052266263644ll : GetAns(2,3);break;
		case 979573735390975739ll : GetAns(2,3);break;
		case 640807389338647549ll : GetAns(2,3);break;
		case 598480316906172486ll : GetAns(3,3);break;
		case 203522456999371050ll : GetAns(2,4);break;
		case 421206431991626060ll : GetAns(2,4);break;
		case 595630806517176908ll : GetAns(2,3);break;
		case 573010858348910652ll : GetAns(3,3);break;
		case 812626144076193076ll : GetAns(2,4);break;
	}
	while(T--){
		int n;scanf("%d",&n);
		printf("%lld\n",1ll*ans[n]*QPow(2,(n-1ll)*(n-1ll))%MOD);
	}
	return 0;
}

T3. 提高组(tg)

[Experience]

想到 DP 了，但就是没有往组合数想……

还好 DP 优秀，虽然只有 20pt，但是还是拿到了这道题场上唯一两个 20 分。

[Solution]

这是一道结论题。

首先我们发现如果 $x<y$ ，把 $x,y$ 交换一下，问题是等价的，也就是说我们只需要考虑 $x\ge y$；

对于一个长度为 $n$ 的满足最长下降子序列的长度不超过 2 的排列，它与一个前缀 max 序列（也就是该序列的第 i 个元素是原序列的前 i 个数的最大值）一一对应。就不证明了……

还有一个结论：x 位置一定是前 x 个数中的最大值。（不想证明，写证明就要写几页）

然后前缀 max 序列满足 mx[i]>=i ，且 mx[n]=n。

然后我们发现，问题变成了这样：

png1

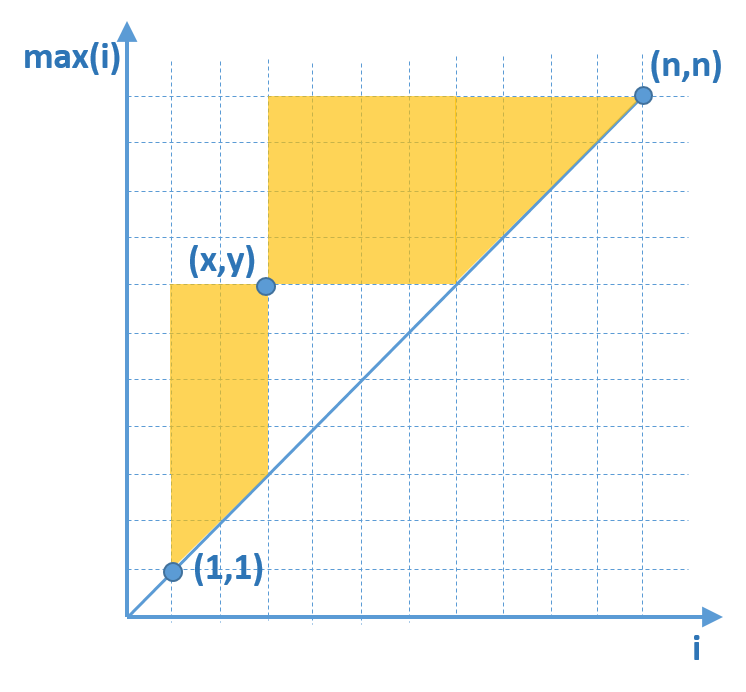
也就是从 (1,1) 出发，经过 (x,y) 到达 (n,n) 且不超过 y=x 这条线的方案数。

很经典的问题，利用卡特兰数的推导方式，我们可以把“不超过 y=x” 改为”不到达 y=x-1” 。即这样：

png2

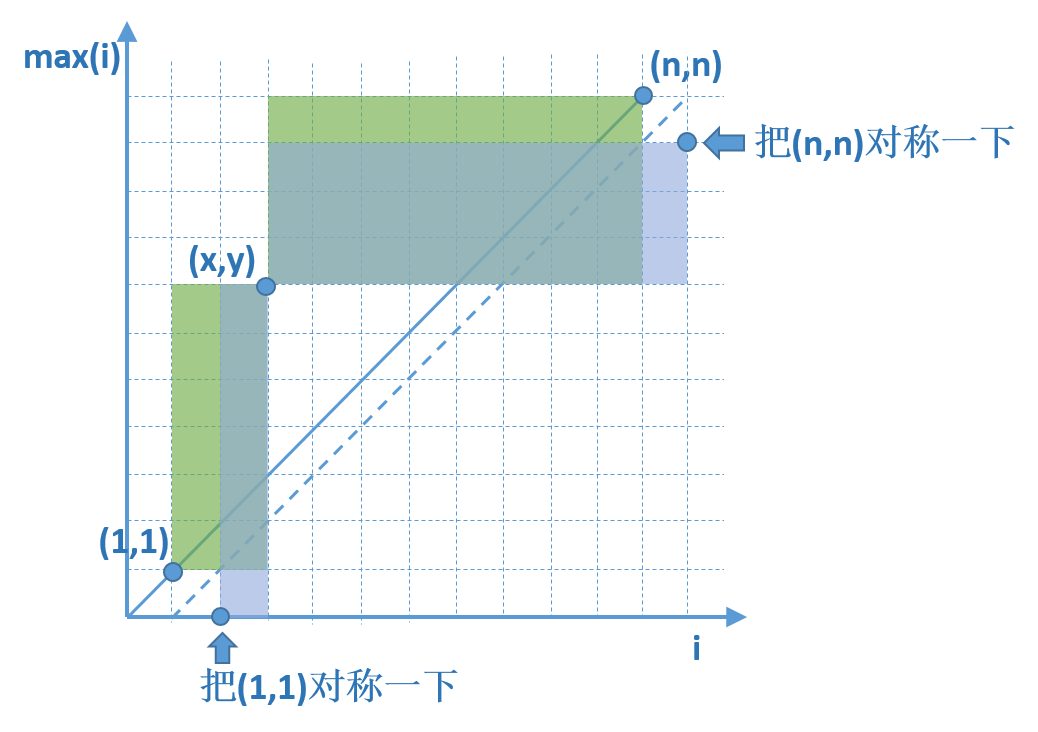
也就是 “从 (1,1) 到 (x,y)” - “从 (2,0) 到 (x,y)” + “从 (x,y) 到 (n,n)” - “从 (x,y) 到 (n+1,n-1)” 。

[Source]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const ll MOD=(ll)1e9+7;
const int N=1e7;

int invfac[2*N+3],fac[2*N+3];

ll fucC(ll a,ll b){
	return 1ll*fac[b]*invfac[a]%MOD*invfac[b-a]%MOD;
}
ll QPow(ll a,ll b){
	ll ret=1;
	while(b){
		if(b&1) ret=ret*a%MOD;
		a=a*a%MOD;
		b>>=1;
	}
	return ret;
}
int main(){
	freopen("tg.in","r",stdin);
	freopen("tg.out","w",stdout);
	fac[0]=1;
	for(int i=1;i<=2*N;i++) fac[i]=(int)((1ll*fac[i-1]*i)%MOD);
	invfac[2*N]=(int)QPow(fac[2*N],MOD-2);
	for(int i=2*N-1;i>=0;i--) invfac[i]=(int)((1ll*invfac[i+1]*(i+1))%MOD);
	int ncas;scanf("%d",&ncas);
	ll ans=0;
	while(ncas--){
		int n,x,y;
		scanf("%d%d%d",&n,&x,&y);
		if(x<y) swap(x,y);
		ll P1x=x,P1y=y,
		   P2x=n,P2y=n,
		   P3x=n-1,P3y=n+1,
		   P4x=0,P4y=2;
		ans=(((fucC(P1x-1,P1y-1+P1x-1)-fucC(P1x-P4x,P1x-P4x+P1y-P4y))%MOD+MOD)%MOD)
		   *(((fucC(P2x-P1x,P2x-P1x+P2y-P1y)-fucC(P3x-P1x,P3x-P1x+P3y-P1y))%MOD+MOD))%MOD;
		printf("%lld\n",ans%MOD);
	}
	return 0;
}

The End

Thanks for reading!

Email: lucky_glass@foxmail.com，欢迎提问~