OI题解 - 优秀的拆分(NOI 2016) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI题解 - 优秀的拆分(NOI 2016)

发表于 更新于 分类于 Valine：

其实可以用 SA/SAM 写，但是我又忘了这俩咋写了 QwQ

# 题意

(既然是中文的题面……)

> 洛谷 P1117

# 解析

由于题目要求找 AABB 式的子串，那么我们可以这样计算——找到一个位置 $i$，然后 $i$ 左边找 AA、右边找 BB，根据乘法原理乘起来就好了。

也就是说要对每个位置 $i$，计算 $l_i,r_i$ 分别表示以 $i$ 开始的 AA（就是 BB，反正形式上是一样的） 的数量和以 $i$ 结束的 AA 的数量。那么答案就是 $\sum l_ir_{i+1}$。

考虑如何迅速计算 $l_i,r_i$。

不妨先枚举 A 的长度 $L\in[1,\frac n2]$，然后把字符串上位置 $L,2L,3L,\dots$ 都打上标记 —— 于是我们发现，任何一个长度为 $2L$ 的 AA 上都有恰好两个位置有标记。

知道这一点有什么用呢？我们枚举相邻两个被标记的位置 $iL,(i+1)L$，想要求经过这两个位置的长度为 $2L$ 的 AA 有哪些。方法就是求 $\Big((i-1)L,iL\Big]$ 和 $\Big(iL,(i+1)L\Big]$ 的最长公共后缀（LCS）、$\Big[iL+1,(i+1)L\Big)$ 和 $\Big[(i+1)L+1,(i+2)L\Big)$ 的最长公共前缀（LCP）。

> Hint. 一定要看清楚这几个串的范围，要不重不漏

画张图可能就好理解了——

jpg1

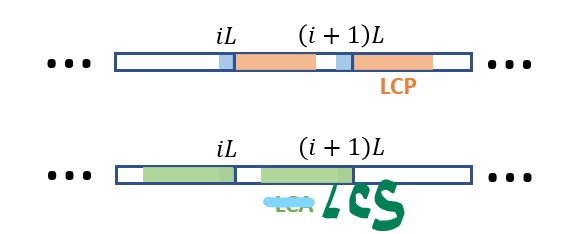
> Update. 我怎么把 LCS 写成 LCA 了 (；′⌒`)

emm……可能需要两张图：

png2

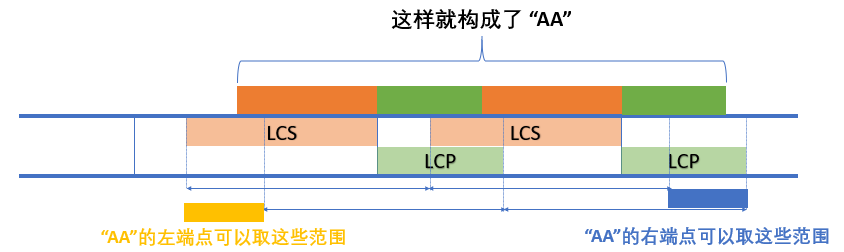
其实已经比较清晰了——我们求出左端点可以取的范围 $[l_1,r_1]$ 和右端点可以取的范围 $[l_2,r_2]$，然后 $l_{[l_1,r_1]}$ 都 +1，$r_{[l_2,r_2]}$ 都 +1，只用差分就好了。

至于怎么求 LCP/LCS，可以用 SA/SAM，但是我忘了怎么写，还好 $O(n\log^2n)$ 能过，可以用哈希+二分来求。

> Hint. 复杂度的话首先是 $O(n)$ 枚举 $L$，然后有 $O(\frac nL)$ 个有标记的位置，每相邻两个标记位置要 $O(\log n)$ 求 LCS,LCP，于是结合求和级数的简单知识，可以知道复杂度是 $O(n\log^2 n)$。

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=3e4,MOD=1e9+7,P=37;

inline int Add(const int a,const int b){return a+b>=MOD? a+b-MOD:a+b;}
inline int Sub(const int a,const int b){return a-b<0? a-b+MOD:a-b;}
inline int Mul(const int a,const int b){return 1ll*a*b%MOD;}
int Pow(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=Mul(ret,a);
        a=Mul(a,a);
        b>>=1;
    }
    return ret;
}

int cas,n;
char str[N+3];
int has[N+3],poP[N+3],inP[N+3];
int cntl[N+3],cntr[N+3];

inline int Part(const int lef,const int rig){
    return Mul(Sub(has[rig],has[lef-1]),inP[lef-1]);
}
int LCS(int r1,int r2){
    int rig=min(r1,r2),lef=0;
    while(lef+1<rig){
        int mid=(lef+rig)>>1;
        if(Part(r1-mid+1,r1)==Part(r2-mid+1,r2)) lef=mid;
        else rig=mid;
    }
    if(Part(r1-rig+1,r1)==Part(r2-rig+1,r2)) return rig;
    return lef;
}
int LCP(int l1,int l2){
    int lef=0,rig=n-max(l1,l2)+1;
    while(lef+1<rig){
        int mid=(lef+rig)>>1;
        if(Part(l1,l1+mid-1)==Part(l2,l2+mid-1)) lef=mid;
        else rig=mid;
    }
    if(Part(l1,l1+rig-1)==Part(l2,l2+rig-1)) return rig;
    return lef;
}
int main(){
    poP[0]=inP[0]=1;
    for(int i=1,inv=Pow(P,MOD-2);i<=N;i++){
        poP[i]=Mul(poP[i-1],P);
        inP[i]=Mul(inP[i-1],inv);
    }
    scanf("%d",&cas);
    while(cas--){
        scanf("%s",str+1);
        n=strlen(str+1);
        for(int i=1;i<=n;i++){
            str[i]-='a'-1;
            has[i]=Add(has[i-1],Mul(str[i],poP[i]));
        }
        for(int len=1;len<=n/2;len++)
            for(int i=len;i<=n;i+=len){
                if(i+len<=n){
                    int lcp=0,lcs=0;
                    if(i+len<=n) lcs=LCS(i,i+len);
                    if(i+len+1<=n) lcp=LCP(i+1,i+len+1);
                    lcs=min(lcs,len);
                    lcp=min(lcp,len-1);
                    if(lcs+lcp>=len){
                        cntl[i-lcs+1]++;
                        cntl[i-(len-lcp)+2]--;
                        cntr[i+len+lcp+1]--;
                        cntr[i+len+(len-lcs)]++;
                    }
                }
            }
        for(int i=1;i<=n;i++){
            cntl[i]+=cntl[i-1];
            cntr[i]+=cntr[i-1];
        }
        cntl[n+1]=cntr[n+1]=0;
        long long ans=0;
        for(int i=1;i<=n;i++){
            ans+=1ll*cntr[i]*cntl[i+1];
            cntl[i]=cntr[i]=0;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

THE END

Thanks for reading!