OI题解 - 矩形(洛谷) | Lucky_Glass's Blog

以心为名，名为爱惜

0%

OI题解 - 矩形(洛谷)

发表于 更新于 分类于 Valine：

百行删尽码复来（指插头DP的代码）

# 题面

> 洛谷 P4537

# 解析

其实这道题用插头DP真的有点小题大做 awa……但是既然在学插头DP，还是用这种方法写一下。

我们发现，题目其实就是要让我们找“有多少条从边界出发、又在边界结束的中间不相交、不接触到边界的折线”，这条折线就会把整个矩形分成黑白两部分，而且可以保证题目中的其他要求。

那用插头DP怎么写？

不妨把原来的矩形看成这样：

png1

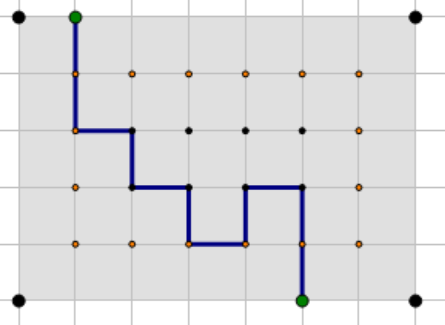
我们不关注这个矩形的方格，而是关注矩形内部（不包括边界）的点，并且我们把最外围的一圈点标为橙色(可见上图)。我们发现，之前提到的一条折线应该是边界的一个点与橙色点相连，中间经过若干个点，最后到达一个橙色点，再到达边界。

于是可以这样考虑：忽略边界与橙色点的连边，那就相当于从橙色点出发再到橙色点。所以可以定义插头DP状态：f[i][j][S][t] 表示从上到下、从左到右一直决定到了点 $(i,j)$，当前的插头状态为 $\mathbb S$，而且当前已经决策出了 $t$ 个橙色点作为起点。

注意这里的 $\mathbb S$，因为我们需要保证最后只有一条中途不相交的线段，所以需要维护插头的连接关系，也就是要用最小表示法或者括号序列来储存。

转移非常麻烦，大概提一下：

设 $nxt$ 是当前位置 $(i,j)$ 相邻的边界的数量

  1. 如果当前位置的上面、左面都有插头，就只能连接“上-左”，此时要判断是否有环以及是否已经得到所需折线（有两个起点 $t=2$，且已经没有插头 $\mathbb S=\varnothing$）
  2. 如果当前位置的上面有插头：
    • 可以连接“上-下”，保证不是最后一行 $i\not= n$；
    • 可以连接“上-右”，保证不是最后一列 $j\not=m$；
    • 如果当前是一个橙色点，并且 $t<2$，可以连接“上-边界”，也就是把当前橙色点作为一个起点，此时还需判断是否已经得到所需折线；
  3. 如果当前位置左面有插头，类似情况 2
  4. 如果当前位置上面左面都没有插头：
    • 可以连接“下-右”，保证不是最后一行、最后一列；
    • 如果当前是橙色点，并且 $t<2$，则可以连接“下-边界”或“右-边界”；
    • 如果当前是橙色点，并且 $t=0$、$(i,j)$ 与至少两个边界相邻、当前还没有连边（$t=0$ 且 $\mathbb S=\varnothing$），则可以连接“边界-边界”，直接得到所需折线；
    • 什么都不连。

反正码码码就对了 (。・∀・)ノ

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long ll;
const int M=1e6;

struct HASH{
    int mem[M],nxt[M],head[3461],MOD,ncnt;
    HASH(){MOD=3461;ncnt=0;}
    void Insert(int x){
        int p=++ncnt,prt=x%MOD;
        nxt[p]=head[prt];mem[p]=x;head[prt]=p;
    }
    int Find(int x){
        for(int it=head[x%MOD];it;it=nxt[it])
            if(mem[it]==x)
                return it;
        Insert(x);
        return ncnt;
    }
    int operator [](int id){return mem[id];}
}Ha;

int n,m;
ll f[2][M][3];
int tmp[20],Tmp[20];

int Inhash(int has){
    int mx=0;
    for(int i=0;i<=m;i++,has>>=3){
        tmp[i]=Tmp[i]=has&7;
        mx=max(mx,tmp[i]);
    }
    return mx;
}
int Hash(){
    int mp[10]={},tot=0;
    for(int i=m;i>=0;i--)
        if(tmp[i]){
            if(!mp[tmp[i]]) mp[tmp[i]]=++tot;
            tmp[i]=mp[tmp[i]];
        }
    int has=0;
    for(int i=m;i>=0;i--)
        has=(has<<3)|tmp[i];
    return Ha.Find(has);
}
void Recover(){
    for(int i=0;i<=m;i++)
        tmp[i]=Tmp[i];
}
int main(){
    scanf("%d%d",&n,&m);
    n--;m--;
    if(!n){
        printf("%d\n",m);
        return 0;
    }
    ll ans=0;
    int I=0;
    f[I][Hash()][0]=1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            I^=1;
            int limS=Ha.ncnt,nxt=(i==1)+(i==n)+(j==1)+(j==m);
            for(int s=1;s<=limS;s++)
                for(int k=0;k<=2;k++)
                    f[I][s][k]=0;
            for(int s=1;s<=limS;s++){
                int mx=Inhash(Ha[s]);
                int lef=tmp[j-1],up=tmp[j];
                for(int k=0;k<=2;k++){
                    ll thi=f[!I][s][k];
                    if(!thi) continue;
                    //左上都有插头，lef!=up 判断了不会成环
                    if(lef && up && lef!=up){
                        Recover();
                        tmp[j]=tmp[j-1]=0;
                        for(int t=0;t<=m;t++)
                            if(tmp[t]==up)
                                tmp[t]=lef;
                        int id=Hash();
                        if(id==1) ans+=thi; //得到所需线段,S=0(S=0 哈希值为1)
                        else f[I][id][k]+=thi;
                    }
                    //有左插头
                    if(lef && !up){
                        //左-下
                        if(i!=n){
                            Recover();
                            tmp[j-1]=lef;tmp[j]=0;
                            f[I][Hash()][k]+=thi;
                        }
                        //左-右
                        if(j!=m){
                            Recover();
                            tmp[j-1]=0;tmp[j]=lef;
                            f[I][Hash()][k]+=thi;
                        }
                        //左-边界
                        if(nxt && k<2){
                            Recover();
                            tmp[j-1]=tmp[j]=0;
                            int id=Hash();
                            if(id==1) ans+=thi*nxt; //连一个边界（有nxt个边界可以选择），得到所需线段
                            else f[I][id][k+1]+=thi*nxt;
                        }
                    }
                    //有上插头，与左插头一样
                    if(up && !lef){
                        if(i!=n){
                            Recover();
                            tmp[j-1]=up;tmp[j]=0;
                            f[I][Hash()][k]+=thi;
                        }
                        if(j!=m){
                            Recover();
                            tmp[j-1]=0;tmp[j]=up;
                            f[I][Hash()][k]+=thi;
                        }
                        if(nxt && k<2){
                            Recover();
                            tmp[j]=tmp[j-1]=0;
                            int id=Hash();
                            if(id==1){
                                // printf("[3] %lld\n",thi*nxt);
                                ans+=thi*nxt;
                            }
                            else f[I][id][k+1]+=thi*nxt;
                        }
                    }
                    //左上都没有
                    if(!lef && !up){
                        //右-下
                        if(i!=n && j!=m){
                            Recover();
                            tmp[j]=tmp[j-1]=mx+1;
                            f[I][Hash()][k]+=thi;
                        }
                        //下-边界，还有插头所以不必判断是否得到答案
                        if(i!=n && nxt && k<2){
                            Recover();
                            tmp[j-1]=mx+1;tmp[j]=0;
                            f[I][Hash()][k+1]+=thi*nxt;
                        }
                        //右-边界，还有插头，同理
                        if(j!=m && nxt && k<2){
                            Recover();
                            tmp[j-1]=0;tmp[j]=mx+1;
                            f[I][Hash()][k+1]+=thi*nxt;
                        }
                        //直接边界-边界得到答案（与两个及以上的边界相邻，还没有起点，没有插头即没有连边）
                        if(nxt>=2 && k==0 && s==1){
                            ans+=nxt*(nxt-1)/2;
                            // printf("[4] %d\n",nxt*(nxt-1)/2);
                        }
                        //啥都不连
                        f[I][s][k]+=thi;
                    }
                }
            }
        }
        //正常的插头DP切换下一行的操作
        I^=1;
        int limS=Ha.ncnt;
        for(int s=1;s<=limS;s++)
            for(int k=0;k<=2;k++)
                f[I][s][k]=0;
        for(int s=1;s<=limS;s++){
            Inhash(Ha[s]);
            if(tmp[m]) continue;
            for(int t=m;t>=1;t--)
                tmp[t]=tmp[t-1];
            tmp[0]=0;
            for(int k=0;k<=2;k++)
                if(f[!I][s][k])
                    f[I][Hash()][k]+=f[!I][s][k];
        }
    }
    printf("%lld\n",ans);
    return 0;
}

THE END

Thanks for reading!