听说以后的练习赛都是 COCI 的题呢(虽然不熟悉这个系列的比赛,但是总觉得特别高级QwQ)
然后这是一道不错的题~
· 题目
温馨提示:题目繁杂,下有翻译
Dominik 想象出了一系列正整数 $P_1 ,P_2 ,…,P_n$ 。让我们将他们排序之后的版本称为 $Q_1 ,Q_2 ,…,Q_n$ 。
此外 , 他想象出了一个允许替换集合 。 如果一对 $(X ,Y)$ 是允许替换集合的成员,Dominik 可以交换数组 $P$ 中位于 $X$ 和 $Y$ 处的数字。
Marin 向 Dominik 进行了 $T$ 次查询,每个查询都属于以下类型之一:
- 把数组 $P$ 中位于 $A$ 和 $B$ 位置的两个数字交换。
- 将 $(A,B)$ 添加到允许替换集合中 。Marin 可能给出已经在允许替换集合中的数对$(A,B)$。
- 看看是否可以仅使用允许替换集合中的替换进行排序?可以以任意顺序使用替换,并且可以使用每个替换任意次数。
- 如果位于 $A$ 位置的数字可以仅使用允许的替换转移到位置 $B$, 那么我们称 $A$ 和 $B$ 是链接的 。 我们把所有和 $A$ 链接的位置构成的集合称为 $A$ 的云 。如果对于一个云中的每个元素 $j$ ,都能在仅使用允许替换集合中的替换使得 $P_j=Q_j$ ,那么我们称这个云是好的 。 你必须回答有多少对不同的满足以下条件的位置 $(A,B)$ :
① 位置 $A$ 和 $B$ 不是链接的;
② $A$ 和 $B$ 的云都不是好的;
③ 如果我们将对 $(A,B)$ 添加到允许的替换集合中,$A$ 的云(通过使 $A$ 和 $B$ 成为链接的来得到)变为好的。请注意:对 $(A,B)$ 和 $(B,A)$ 被认为是完全相同的一对位置。
· 解析
- 题意
我觉得为了reader们读题不这么懵逼,还是翻译一下题目……
有一个包含 $n$ 个数的数组 $P$ ,将它从小到大排序后我们会得到数组 $Q$ 。
我们现在对 $P$ 的一些位置(不是数字)进行操作:
- 给定 正整数$A,B$ ,交换 $P$数组 的 $A$位置 和 $B$位置 上的数;
- 给定 正整数$A,B$,我们把 $A$位置 和 $B$位置 连接起来。
- 如果 $A,B$ 位置是连接的,那么我们可以交换 $P$数组 $A$位置 和 $B$位置 上的数;问能否通过若干次交换,使 $P$数组 与 $Q$数组 相同(只需要各个位置的数值相等)。如果能,输出 “DA”,否则输出 “NE”。
定义“云”为一个集合,当且仅当 $A$位置 和 $B$位置 直接或间接相连,$A$ 和 $B$ 属于一个云。换个说法,如果我们把 “连接$A位置,B位置$” 看成 “在 $A位置,B位置$ 之间连一条边”,那么一个云就是一个连通块。
定义一个云$A$是“好”的,当且仅当$\{P_i|i\in A\}=\{Q_i|i\in A\}$。
求解有多少个数对 $(X,Y)$ 满足以下条件:(在这里 $(X,Y)$ 和 $(Y,X)$ 没有区别)
- $X,Y$ 不在同一个云内;
- $X,Y$ 所在的云都不是好的;
- 若连接 $X,Y$,则 $X,Y$ 原本所在的云合为一个云,满足合并得到的云是好的。
- 处理云
按照定义,可以发现在没有进行任何操作的时候,每个位置各自属于一个云。
当我们连接 $A,B$位置 时,$A$ 所在的云 就和 $B$所在的云 合并了……支持合并操作的数据结构?——并查集。
最初每个位置都是一个并查集,也就是 $cld_i=i$ ($cld$数组是并查集数组,如果$cld_i=cld_j$,那么$i,j$在同一个并查集里);当我们连接 $A,B$ 时,只需要把 $A,B$ 所在并查集合并就行了。
对于并查集$A$,我们定义:
- $siz_A$ 表示并查集的大小;
- $cldP_A$ 是一个数组:数组的第 $x$ 个元素的值是 “并查集中满足 $P_t=x$ (还记得数组$P$吗?就是题目中提到的那个)的元素$t$的个数”;
- $cldQ_A$ 是一个数组:数组的第 $x$ 个元素的值是 “并查集中满足 $Q_t=x$ (还记得数组$Q$吗?就是题目中提到的那个)的元素$t$的个数”;
下面我们考虑怎么合并并查集$X$和并查集$Y$。(也就是合并云$X$和云$Y$)
首先 $cld_Y=X$,这是我自己的做法——把$Y$的数据合入$X$里。
然后 $cldP_X$ 和 $cldP_Y$ 的对应位置相加,并且 $cldQ_X$ 和 $cldQ_Y$ 的对应位置相加,也就是 $Y$ 的所有元素与 $X$ 的元素合并。
最后 $siz_X+=siz_Y$,也就是更新合并后的并查集大小。
- 哈希合并加速
我们会发现在合并并查集$X,Y$时,由于我们要将 $cldP$ 和 $cldQ$ 的对应位置相加,这个操作就会变成 $O(n)$ 的,在多次询问的情况下肯定是会 TLE 的,所以我们考虑哈希——
定义一个质数常数 $prn$ ,我这里取用的是 $prn=1000016107$ (是随便取的一个大于 $10^9$ 的数)。
然后把 $cldP$ 数组的第 $i$ 个元素作为一个 $prm$ 进制数的第 $i$ 位,以这个 $prm$进制数 作为 $cldP$ 的哈希值。哈希值用unsigned long long储存,自然溢出。
对于 $cldQ$ 也这样处理。
这样我们就把 $cldP,cldQ$ 由数组转换为数字。而且因为它只是一个 $prm$进制数,合并 并查集$X,Y$ 时只需要让 $cldP_X+=cldP_Y,cldQ_X+=cldQ_Y$ 就可以了。
这样操作1,2不就 $O(1)$ 了吗?
- 查询加速
= 加速操作 3
由于时间限制,我们不可能每次操作3时,都模拟排序一遍。
但是我们知道,当且仅当每一个云都是好的,经过若干次交换后,$P$可以变得和 $Q$ 相同。
所以我们定义 $numgood$ 是好的云的个数,$numcld$ 是云的总个数(因为合并云的时候云的个数会减一,所以储存 $numcld$ 是有必要的)。当 $numgood=numcld$ 时,经过若干次交换,$P$ 可以变为 $Q$。
只有交换元素或合并云(操作1,2)的时候 $numgood$ 会改变——所以在交换 $X,Y$ 中的元素或合并 $X,Y$ 时,我们先在 $numgood$ 中减去 $X,Y$ 中好的云的个数,交换或合并完后,我们把得到的云中好的云的个数加回 $numgood$ 里。
这样就实现操作 3 $O(1)$ 了!
= 加速操作 4
这是最复杂的一个操作。
可以发现如果数对 $(i,j)$ 满足操作4的要求(忘了要求的上去看题目),那么 $i$ 所在云$X$ 中的每个元素与 $j$ 所在云$Y$中的每个元素都可以构成一个符合要求的数对。
那么我们就不单个考虑元素,而是考虑一对云。根据定义,我们可以知道:当且仅当 $X,Y$都不是好的云 且 $cldP_X+cldP_Y=cldQ_X+cldQ_Y$ 时,$X$的每个元素 与 $Y$的每个元素 都能构成一个符合要求的数对(下文简称“$X$的每个元素 与 $Y$的每个元素 都能构成一个符合要求的数对”为“$X,Y$配对”)。
我们把 $cldP_X+cldP_Y=cldQ_X+cldQ_Y$ 变一下形—— $cldP_X-cldQ_X=cldQ_Y-cldP_Y$ 。也就是说当 $X,Y$ 满足 $cldP_X-cldQ_X=cldQ_Y-cldP_Y$ 且 $X,Y$都不是好的云 时,$X,Y$ 配对,则可以构造出 $siz_X\times siz_Y$ 个数对。
定义 $cnt_i$ 表示所有 $cldP_X-cldQ_X=i$ 的云$X$的元素个数之和。对于 云$X$ ,它包含的每个元素可以和 $cnt_{cldQ_X-cldP_X}$ 个元素构成一个数对,那么云$X$对操作4的答案的“贡献”为 $siz_X\times cnt_{cldQ_X-cldP_X}$ 。
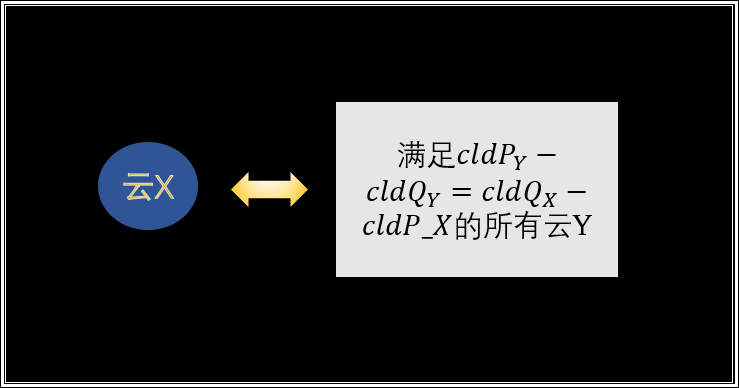
记操作4的答案为 $numpair$ (注意这道题的 numpair 要开 long long)。
显然仍然只会在操作1,2时 $numpair$ 会改变。
操作1
假设要交换数字的两个位置分别属于云$X,Y(X\not=Y)$ 。
那么在交换之前,我们在分别减去 $X,Y$ 对 $numpair$ 的贡献:
(如果$X$不是好云)$numpair-=siz_X\times cnt_{cldQ_X-cldP_X}$
(如果$Y$不是好云)$numpair-=siz_Y\times cnt_{cldQ_Y-cldP_Y}$
但是就出现了一个问题:如果 $X,Y$ 是配对的呢?
因为题目所求的数对是无序的,所以当 $X,Y$ 配对时,我们就多减了一个 $X,Y$ 之间的贡献,就像容斥原理一样,我们需要把多减去的贡献加回去:$numpair+=siz_X\times siz_Y$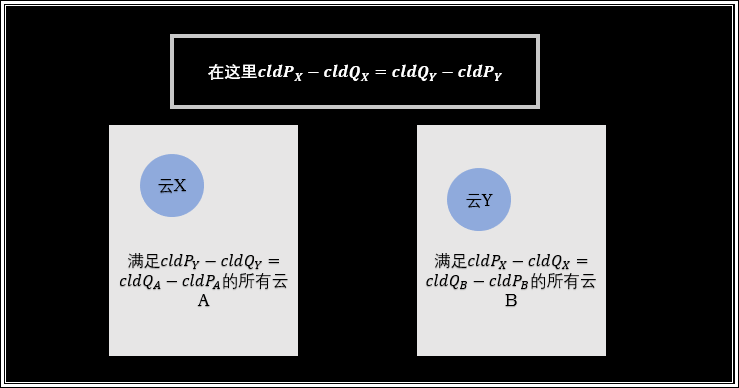
在交换之后,先更新 $cnt,cldP$ 。
再用同样的操作将修改后$X,Y$ 分别的贡献加到 $numpair$ 上去。
操作2
先分别减去 $X,Y$ 对 $numpair$ 的贡献,与操作1相同。
合并后先更新 $cnt,cldP$ ,再加入合并后得到的$X$云对 $numpair$ 的贡献,即 $numpair+=siz_X\times cnt_{cldQ_X-cldP_X}$ 。
查询时输出 $numpair$ 就好啦~
这不就 $O(1)$ 了吗?
(其实我的代码是 $O(log n)$,因为我用的 map 储存 $cnt$ ,不然就还要写一个哈希来处理 $cnt$ 数组的大下标)
· 源代码
1 | /*Lucky_Glass*/ |
The End
Thanks for reading!
Email: lucky_glass@foxmail.com ,欢迎提问~